Kapitel
- Winkelfunktionen eines rechtwinkligen Dreiecks
- Winkelfunktionen eines Kreises
- Vorzeichen der Winkelfunktionen
- Tabelle der Winkelfunktionen
- Satz des Pythagoras und Winkelfunktionen
- Beziehungen zwischen Winkelfunktionen und Winkeln
- Winkelfunktionen – Addition und Subtraktion von Winkeln
- Winkelfunktionen des doppelten Winkels
- Winkelfunktionen des halben Winkels
- Umwandlung Summe – Produkt
- Umwandlung Produkt – Summe
- Aufgaben zur Berechnung von Sinus, Kosinus und Tangens
Winkelfunktionen eines rechtwinkligen Dreiecks
Sinus
Der Sinus des Winkels B ist das Verhältnis der Länge der Gegenkathete zur Länge der Hypotenuse. Die Bezeichnung lautet sin b.
Kosinus
Der Kosinuns des Winkels B ist das Verhältnis der Länge der Ankathete zur Länge der Hypotenuse.
Die Bezeichnung lautet cos b.
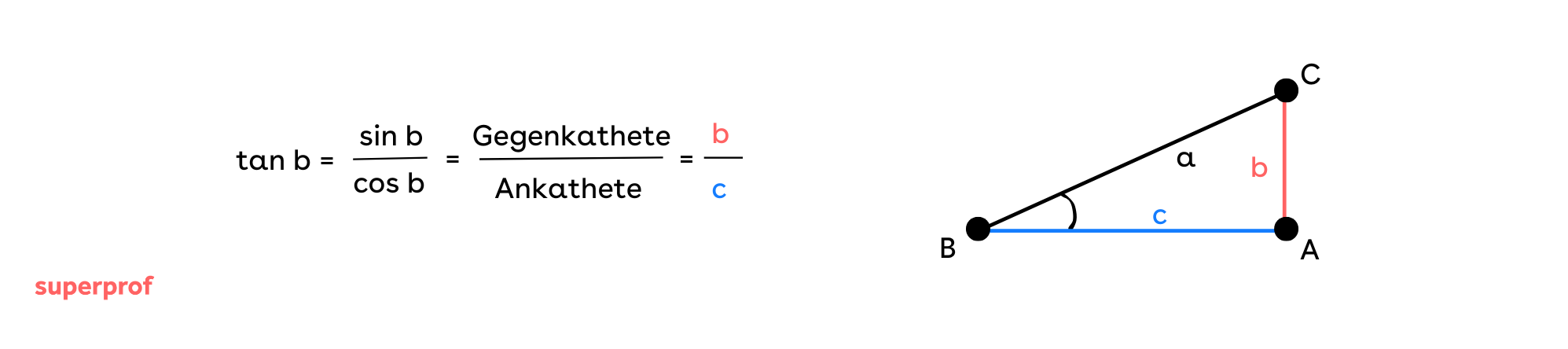
Tangens
Der Tangens des Winkels B ist das Verhältnis der Länge der Gegenkathete zur Länge der Ankathete.
Die Bezeichnung lautet tan b.
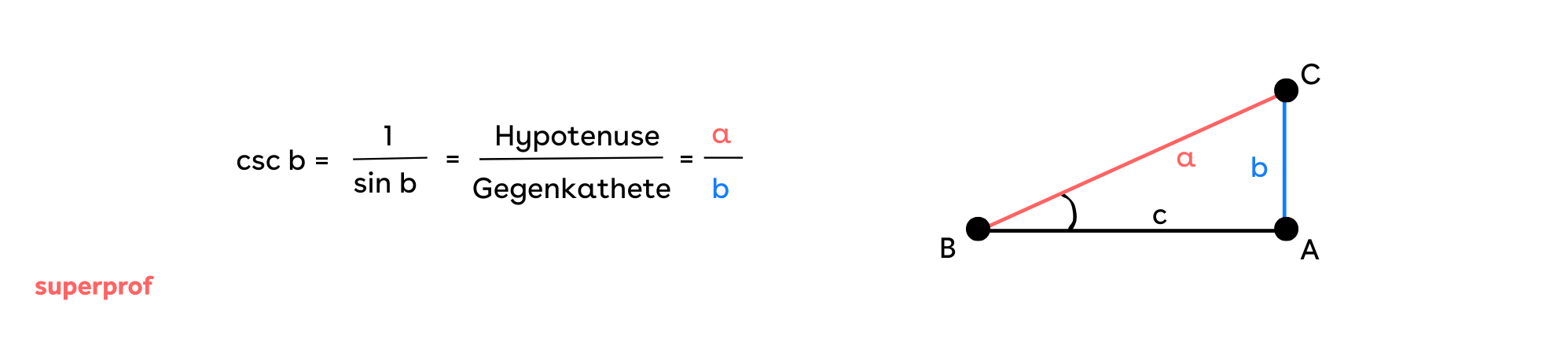
Kosekans
Der Kosekans des Winkels B ist die Kehrwert-Funktion der Sinus-Funktion von B.
Die Bezeichnung lautet csc b.
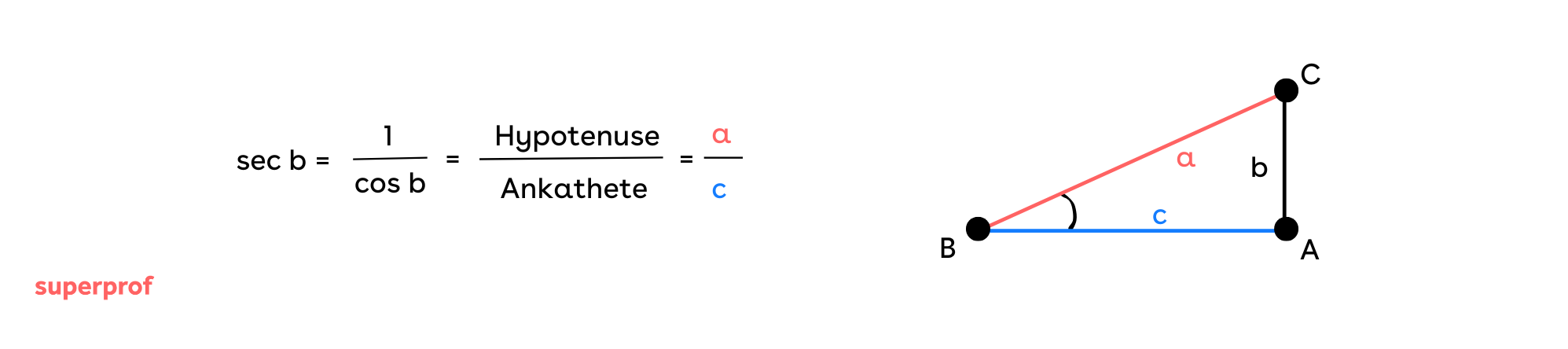
Sekans
Der Sekans des Winkels B ist die Kehrwert-Funktion der Kosinus-Funktion von B.
Die Bezeichnung lautet sec b.
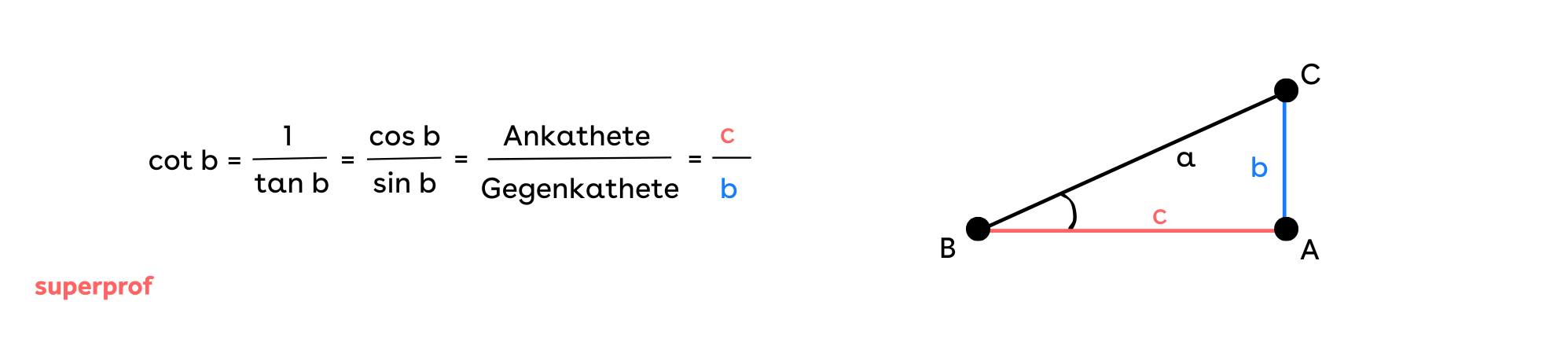
Kotangens
Der Kotangens des Winkels B ist die Kehrwert-Funktion der Tangens-Funktion von B.
Die Bezeichnung lautet cot b.
Eine Hilfestellung ist, sich zu merken, dass der Kosekans, der Sekans und der Kotangens die Kehrwertfunktion von Sinus, Kosinus und Tangens sind. Sieh dir hierzu folgende Tabelle an:
Winkelfunktionen eines Kreises
Der Einheitskreis hat seinen Mittelpunkt im Koordinatenursprung und sein Radius ist die Einheit.
Wir sehen uns ein rechtwinkliges Dreieck an, das in einem Kreis liegt. Dessen Radius bildet die Hypotenuse und eine der Katheten liegt auf der x-Achse.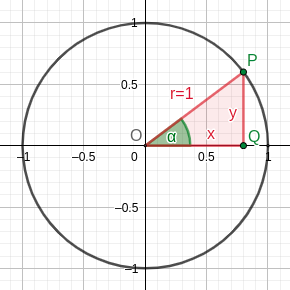
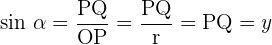
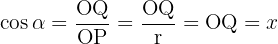
Wir kommen zu folgendem Ergebnis:
Der Sinus ist die y-Achse von P, d.h. des Punktes, der auf dem Kreis liegt.
Der Kosinus ist die x-Achse von P, d.h. des Punktes, der auf dem Kreis liegt.
Eine weitere Tatsache, die wir ableiten können, ist, dass die Werte von Sinus und Kosinus zwischen 1 und -1 liegen.
-1 ≤ sin α ≤ 1
-1 ≤ cos α ≤ 1
Es sei darauf hingewiesen, dass der Grund für die Betrachtung trigonometrischer Funktionen auf dem Kreis darin liegt, dass man größere Winkel nehmen kann. Zum Beispiel können wir von einem rechtwinkligen Dreieck nicht ableiten, wieviel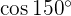 
ist, da kein rechtwinkliges Dreieck mit einem Winkel von 150°gebildet werden kann.
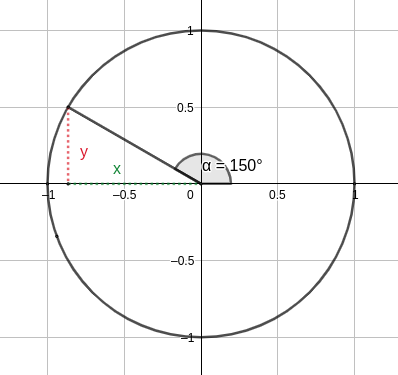
Mit dem Einheitskreis können wir diese Berechnung allerdings durchführen:
1 Wir legen den Winkel von 150°, der von der X-Achse aus gebildet wird, gegen den Uhrzeigersinn fest.
2 Wir sehen uns den Punkt auf dem Kreis an, der mit dem Winkel Folgendes darstellt:
- Die y-Achse dieses Punktes ist der Sinus
- Die x-Achse ist der Kosinus
Für die weiteren Winkelfunktionen sehen wir uns folgende Grafik an
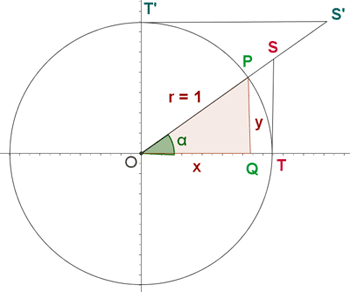
QOP und TOS sind zueinander ähnliche Dreiecke. Somit gilt
QOP und T'OS′ sind zueinander ähnliche Dreiecke. Somit gilt
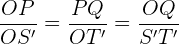
Mit Hilfe der Definitionen der Winkelfunktionen und der Beziehungen zwischen ähnlichen Dreiecken erhalten wir
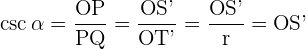
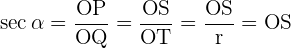
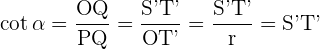
Vorzeichen der Winkelfunktionen
Auf dem Einheitskreis begrenzen die Koordinatenachsen vier Quadranten, die gegen den Uhrzeigersinn nummeriert sind. Wir denken daran, dass, wenn wir einen Winkel betrachten und das rechtwinklige Dreieck innerhalb des durch diesen Winkel gebildeten Kreises nehmen, das Vorzeichen des Sinus oder Kosinus dieses Winkels davon abhängt, in welchem Quadranten sich das Dreieck befindet.
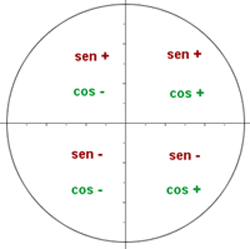
Tabelle der Winkelfunktionen
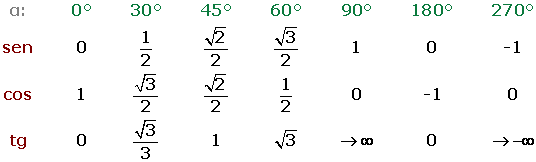
Satz des Pythagoras und Winkelfunktionen
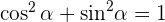
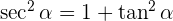
Erklärung:
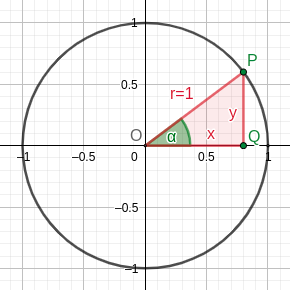
Da das betrachtete Dreieck im Inneren des Kreises ein rechtwinkliges Dreieck ist, gilt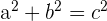
In der Grafik entsprechen die Katheten (a und b) den Werten x und y, und die Hypotenuse dem Radius, also 1.
Somit gilt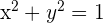 
Da x die x-Achse und y die y-Achse ist, wissen wir, dass diese Werte jeweils dem Sinus und dem Kosinus entsprechen. Somit gilt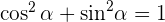
Wir dividieren die vorhergehende Gleichung durch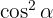 
und erhalten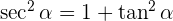
Wenn wir stattdessen durch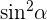 
dividiert hätten, wäre das Ergebnis
Beziehungen zwischen Winkelfunktionen und Winkeln
Komplementwinkel
Zwei Winkel werden Komplementwinkel genannt, wenn ihre Summe 90° ist, also ein rechtwinkliger Winkel.
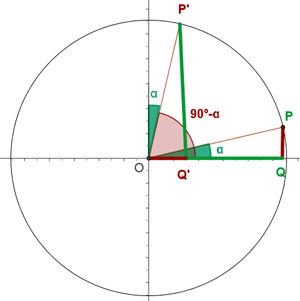
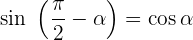
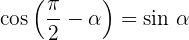
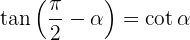
Supplementwinkel
Zwei Winkel werden Supplementwinkel genannt, wenn ihre Summe 180° ist.
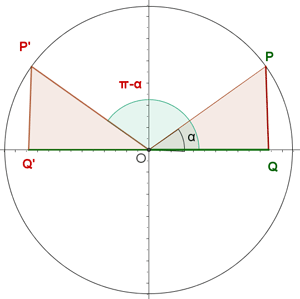
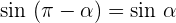
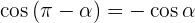
Winkel, die sich um 180° unterschieden
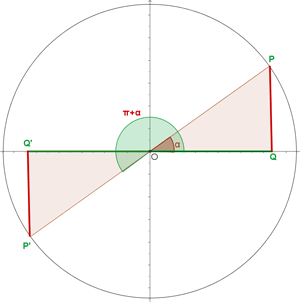
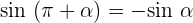
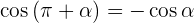
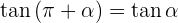
Gegenwinkel
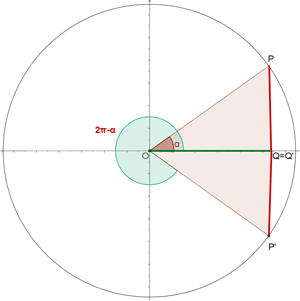
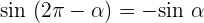
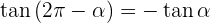
Negative Winkel
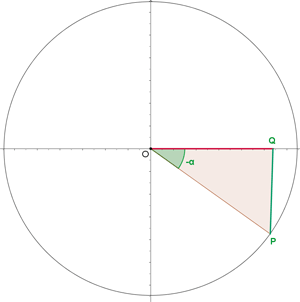
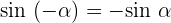
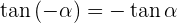
Größer als 360º
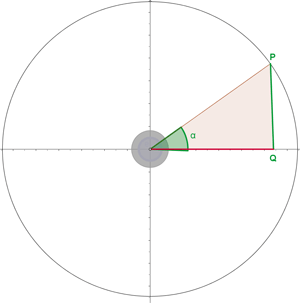
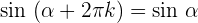
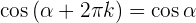
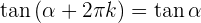
Winkel, die sich um 90º unterscheiden
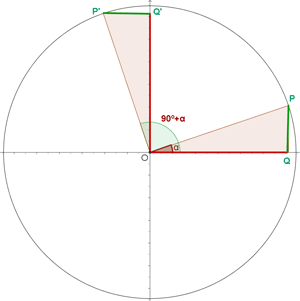
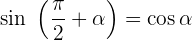
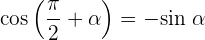
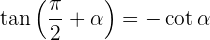
Winkel, die 270º ergeben
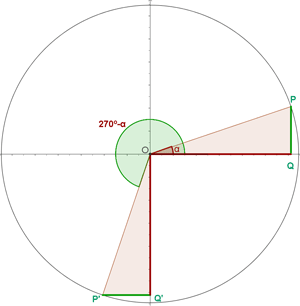
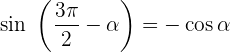
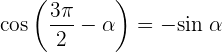
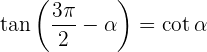
Winkel, die sich um 270º unterscheiden
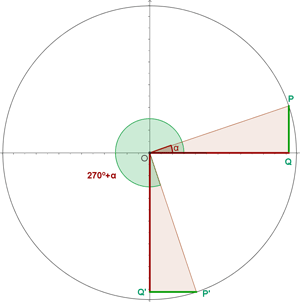
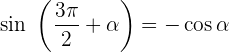
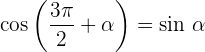
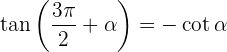
Winkelfunktionen – Addition und Subtraktion von Winkeln
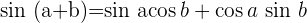
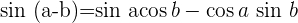
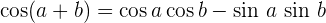
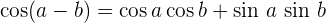
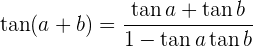
Winkelfunktionen des doppelten Winkels
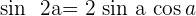
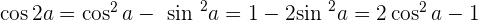
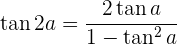
Winkelfunktionen des halben Winkels
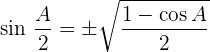
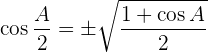
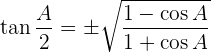
Umwandlung Summe – Produkt
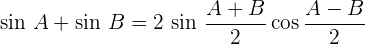
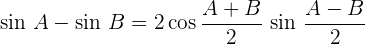
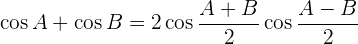
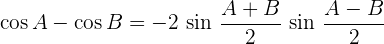
Umwandlung Produkt – Summe
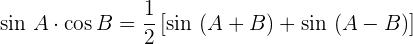
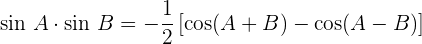
Aufgaben zur Berechnung von Sinus, Kosinus und Tangens
Berechne Sinus, Kosinus und Tangens von 
:
1 Sinus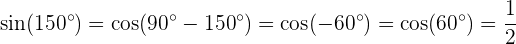
2 Kosinus
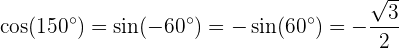
3 Tangens
Berechne Sinus, Kosinus und Tangens von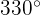 
:
1 Sinus
2 Kosinus
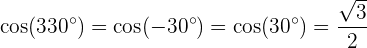
3 Tangens
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
