Löse folgende Aufgaben:
Um das Wasser aus einem Kunststoffbecken zu entfernen, sind 210 Entnahmen mit einem Eimer von 
Litern Inhalt erforderlich. Wenn der Eimer ein Fassungsvermögen von 
Litern hat, wie viele Entnahmen sind dann erforderlich, um das gesamte Wasser aus dem Becken zu entfernen?
Entnahmen
Dieses Feld ist erforderlich.
Dies ist ein umgekehrter Dreisatz, denn je mehr Fassungsvermögen des Eimers, desto weniger Entnahmen.
Es sind 
Entnahmen nötig.
Mit 
kg Futter können 
Hühner 
Tage lang gefüttert werden. Wenn 
Hühner sterben, wie lange reicht dann das Futter?
Tage
Dieses Feld ist erforderlich.
Dies ist ein umgekehrter Dreisatz, denn weniger Hühner bedeuten mehr Tage, an denen es Futter gibt.
Wenn Hühner sterben, bleiben noch 
Hühner übrig.
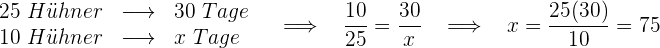
Das Futter reicht also für 
Tage.
Ein Pizzabote braucht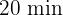 
für eine Lieferung, wenn er mit einer Geschwindigkeit von 
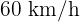fährt. Wenn er höchstens 
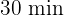Zeit für die Lieferung hat, mit welcher Mindestgeschwindigkeit muss er fahren, um die Lieferung in der maximalen Zeit zu schaffen?
.
Dieses Feld ist erforderlich.
Dies ist ein umgekehrter Dreisatz, denn je niedriger die Geschwindigkeit, desto länger die Zeit.
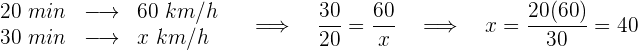
Die Mindestgeschwindigkeit beträgt 
Drei Arbeiter führen eine Arbeit in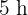 
aus. Wie lange brauchen zwei Arbeiter für dieselbe Arbeit?
.
Dieses Feld ist erforderlich.
Dies ist ein umgekehrter Dreisatz, denn je weniger Arbeiter es gibt, desto länger dauert es.
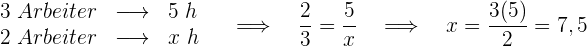
Die Zeit, die zwei Arbeiter für diese Arbeit benötigen, beträgt 
Drei Mechaniker bauen einen Motor in 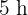zusammen. Wenn es fünf Mechaniker sind, wie lange brauchen sie, um den Motor zusammenzubauen?
.
Dieses Feld ist erforderlich.
Dies ist ein umgekehrter Dreisatz, denn je mehr Mechaniker, desto weniger Zeit.
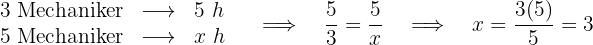
Die Zeit, die fünf Mechaniker für den Zusammenbau des Motors benötigen, beträgt 
Ein Läufer läuft eine 
-Runde in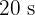 
mit einer Geschwindigkeit von 
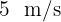. Wie lange benötigt er für die Runde, wenn er seine Geschwindigkeit auf 
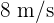erhöht?
.
Dieses Feld ist erforderlich.
Dies ist ein umgekehrter Dreisatz, denn je höher die Geschwindigkeit, desto kürzer die Zeit.
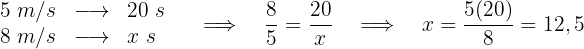
Die Zeit für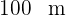 
beträgt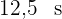 
Eine Lehrerin plant, jedem ihrer Schüler*innen vier Bonbons zu geben. Wenn sie 21 Schüler*innen hat, aber nur 12 anwesend sind und sie beabsichtigt, alle Bonbons gleichmäßig zu verteilen, wie viele Bonbons bekommt dann jede*r Schüler*in?
Bonbons.
Dieses Feld ist erforderlich.
Dies ist ein umgekehrter Dreisatz, denn je weniger Schüler*innen anwesend sind, desto mehr Süßigkeiten gibt es.
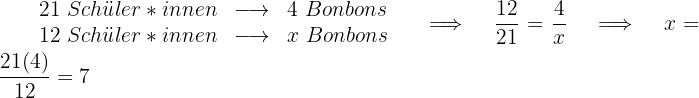
Jede*r Schüler*in bekommt 
Bonbons.
Drei Arbeiter führen eine Arbeit in 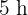aus. Wenn sieben weitere Arbeiter zur Unterstützung kommen, wie lange brauchen sie dann alle für dieselbe Arbeit?
.
Dieses Feld ist erforderlich.
Dies ist ein umgekehrter Dreisatz, denn je mehr Arbeiter vorhanden sind, desto weniger Zeit wird benötigt, um die Arbeit zu erledigen.
Beachte, dass es sich um eine ähnliche Aufgabe wie in Aufgabe 4 handelt, mit dem Unterschied, dass die Anzahl der Arbeiter nicht abnimmt, sondern zunimmt.
Da Arbeiter dazukommen, sind insgesamt Arbeiter vorhanden
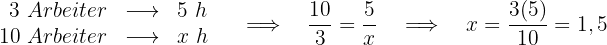
Die benötigte Zeit für 10 Arbeiter beträgt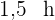 
Mit kg Futter können Hühner Tage lang gefüttert werden. Wenn 
Hühner dazukommen, wie lange reicht dann das Futter?
Tage
Dieses Feld ist erforderlich.
Dies ist ein umgekehrter Dreisatz, denn mehr Hühner bedeuten weniger Tage, an denen es Futter gibt.
Beachte, dass es ähnlich wie bei Aufgabe 2 ist, mit dem Unterschied, dass sich die Anzahl der Hühner nicht verringert, sondern erhöht.
Wenn die Zahl der Hühner um erhöht wird, bleiben Hühner übrig, die zu füttern sind.
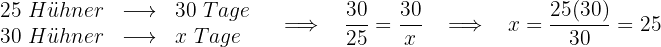
Das Futter reicht für Tage.
Johannes und Peter beteiligen sich jeweils mit 
€ am Kauf eines Geschenks. Wenn sich Maria auch an dem Geschenk beteiligen möchte, wie hoch ist dann der jeweilige Anteil?
€.
Dieses Feld ist erforderlich.
Es handelt sich um einen umgekehrten Dreisatz, denn je mehr Personen teilnehmen, desto niedriger ist der zu zahlende Betrag.
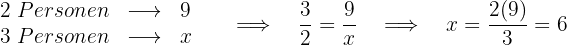
Jeder trägt 
€ zum Geschenk bei.
Fünf Personen brauchen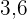 
Tage, um eine Mauer zu bauen. Wenn zwei von ihnen krank werden, wie viele Tage dauert es dann, um die Mauer zu bauen?
Tage.
Dieses Feld ist erforderlich.
Dies ist ein umgekehrter Dreisatz, denn je weniger Personen teilnehmen, desto mehr Tage werden benötigt.
Da zwei Personen krank sind, gibt es nur noch drei Personen, die die Arbeit erledigen.
Die drei Personen benötigen Tage zum Bau der Mauer.
Peter arbeitet pro Tag 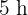an seinem Schulprojekt und braucht somit sechs Tage, um es fertigzustellen. Wie lange braucht er für sein Projekt, wenn er am Tag nur 
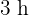daran arbeitet?
Tage.
Dieses Feld ist erforderlich.
Dies ist ein umgekehrter Dreisatz, denn je weniger Stunden pro Tag, desto mehr Tage werden für die Fertigstellung des Projekts benötigt.
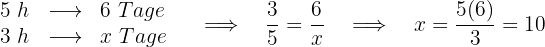
Peter benötigt Tage für sein Projekt, wenn er 
pro Tag daran arbeitet.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
