Kapitel

Wichtige Hilfsmittel zur Lösung der Aufgaben
Um die folgenden Übungen lösen zu können, benötigen wir folgende Hilfsmittel:
- Einheitskreis
- Grundlegende trigonometrische Identitäten
- Pythagoreische trigonometrische Identitäten
- Gerade und ungerade trigonometrische Identitäten
- cTrigonometrische Identitäten für Doppelwinkel
- Trigonometrische Identitäten für Halbwinkel
- Addition und Subtraktion von Winkeln und Beziehungen zwischen Produkt und Summe
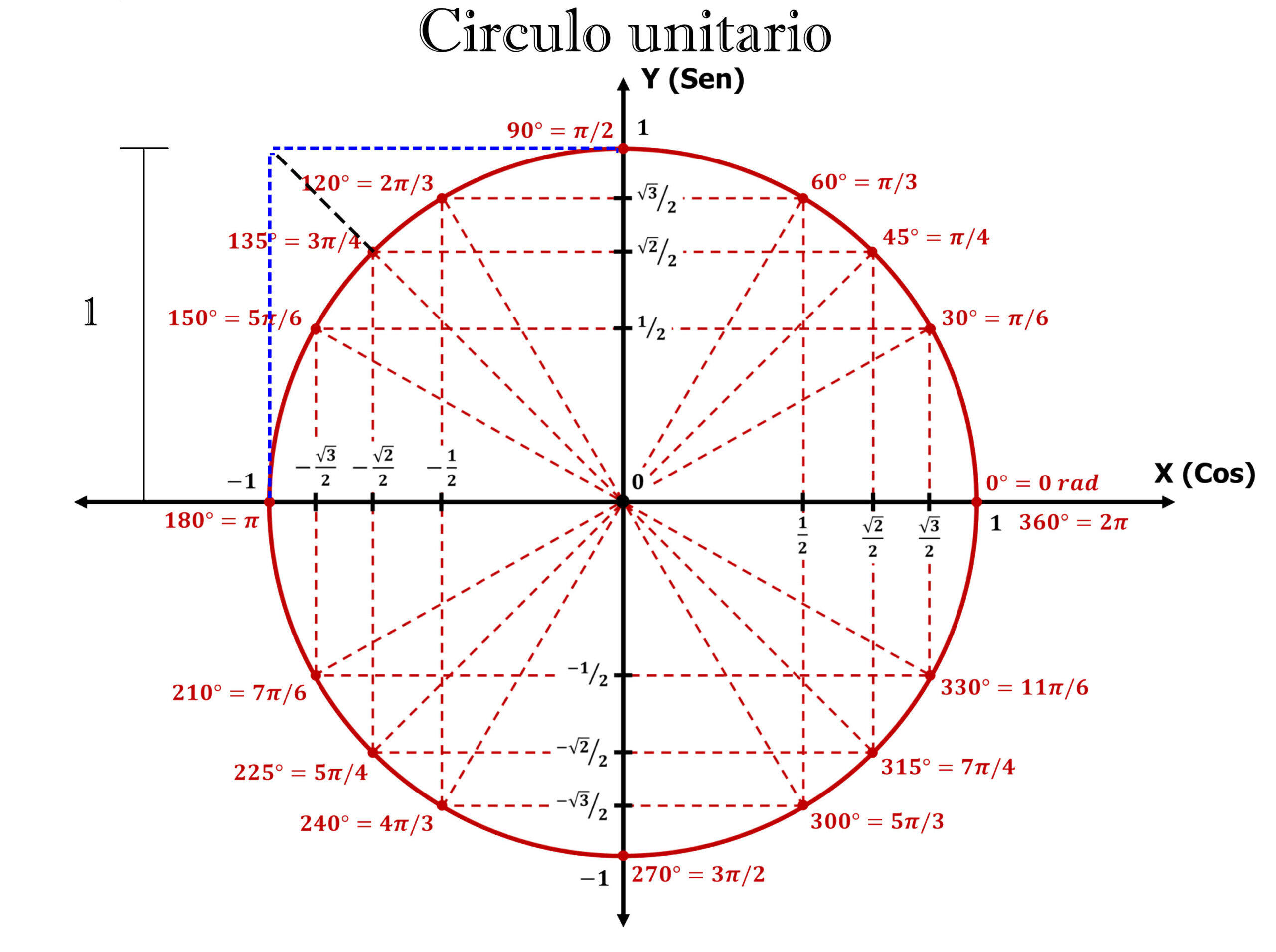
Einheitskreis
Die als Einheitskreis bekannte Tabelle enthält die repräsentativsten Radiuswerte, die in der Trigonometrie verwendet werden. Der Name dieses Kreises leitet sich davon ab, dass es sich um einen Kreis mit dem Radius 1 handelt.
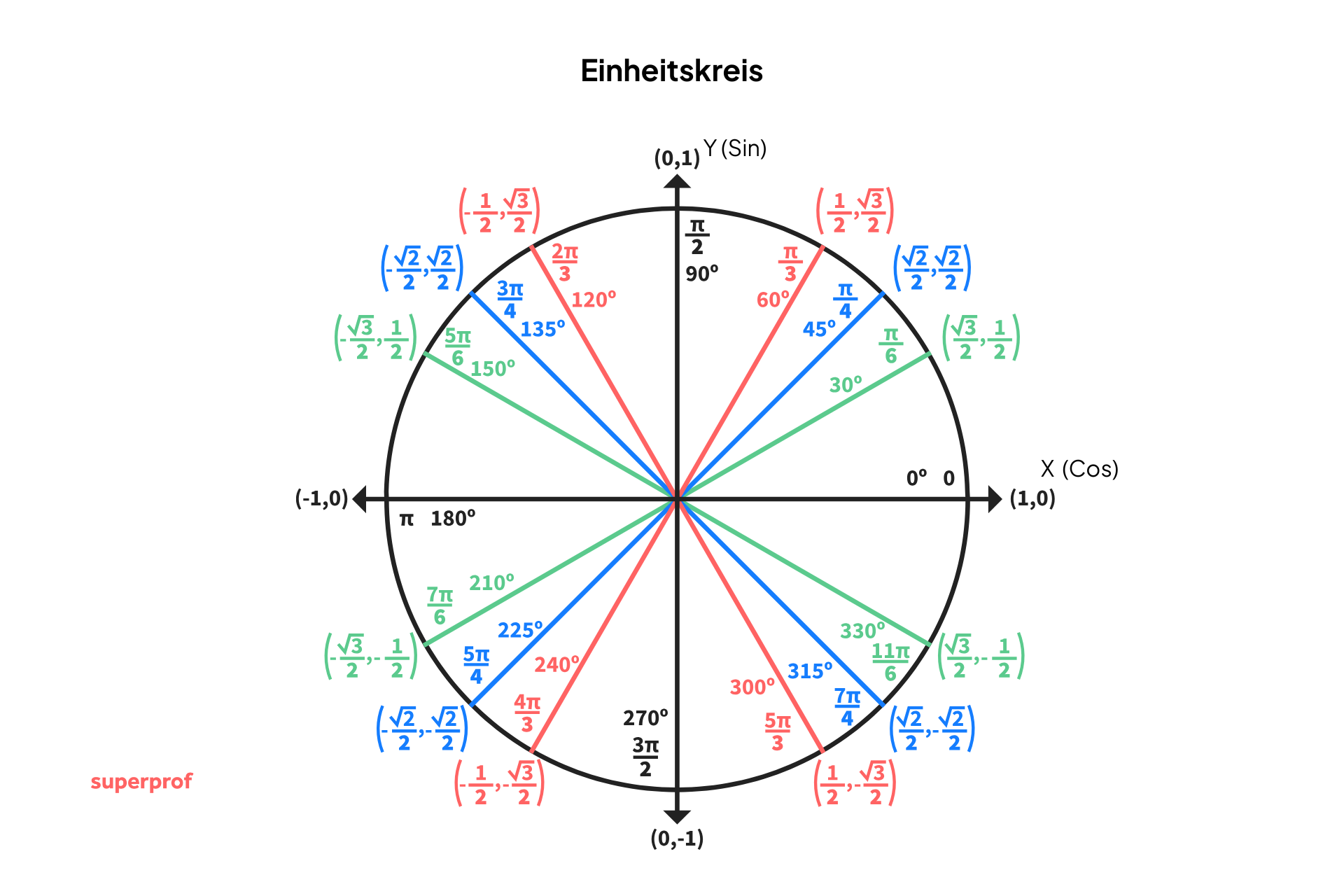
Mit diesem Hilfsmittel lässt sich der Wert der Winkel ganz einfach ermitteln. Wenn wir zum Beispiel den Wert von 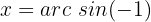 ermittlen möchten, müssen wir uns einfach auf die Sinus-Achse konzentrieren. Das heißt, die y-Achse, und uns schließlich den Wert von
ermittlen möchten, müssen wir uns einfach auf die Sinus-Achse konzentrieren. Das heißt, die y-Achse, und uns schließlich den Wert von  ansehen.
ansehen.
Wir stellen fest, dass der Winkel laut Tabelle que la tabla indica que el angulo es 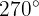 misst. Dies ist der Wert in Grad, jedoch existiert der Wert auch in Radiant, welcher
misst. Dies ist der Wert in Grad, jedoch existiert der Wert auch in Radiant, welcher 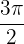 ist.
ist.
Wenn wir die Werte für die Tangente bestimmen müssen, denken wir daran, dass die Tangente eine Gerade ist, die den Kreis in einem einzigen Punkt berührt. Im Falle dieses Kreises wird die Tangente verwendet, die den Punkt in  berührt und die Höhe der Tangente hängt vom Wert in der Gleichung ab. Zum Beispiel bestimmen wir in der Gleichung
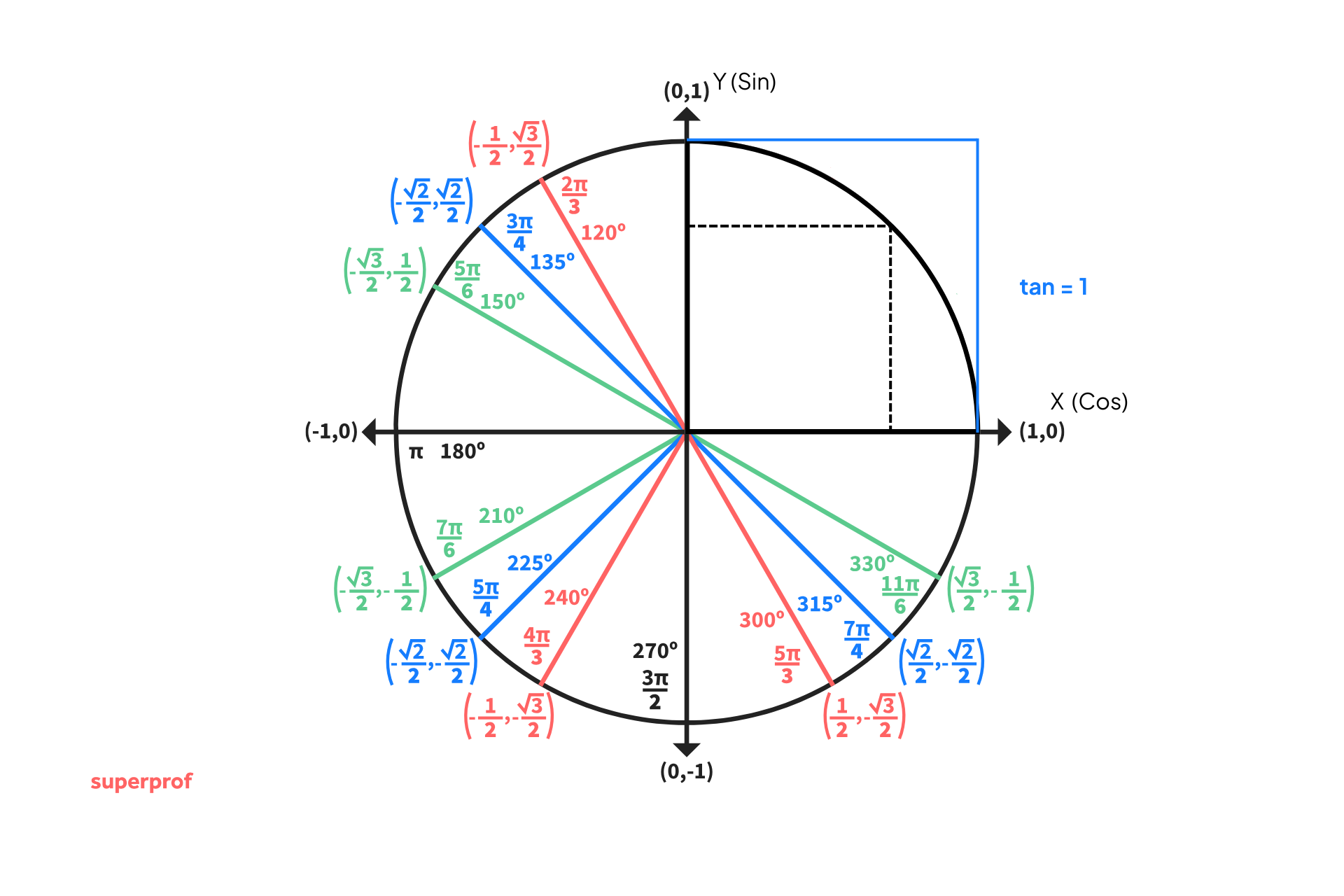
berührt und die Höhe der Tangente hängt vom Wert in der Gleichung ab. Zum Beispiel bestimmen wir in der Gleichung  die Variable und erhalten
die Variable und erhalten 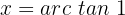 . Wir suchen also die Tangente der Höhe
. Wir suchen also die Tangente der Höhe  und ziehen eine Linie zum Ursprung. Wir betrachten den Schnittpunkt mit dem Kreis und suchen den Wert in der Tabelle.
und ziehen eine Linie zum Ursprung. Wir betrachten den Schnittpunkt mit dem Kreis und suchen den Wert in der Tabelle.
Entspricht 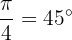
Man könnte auch sagen, dass er 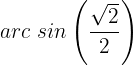 oder
oder 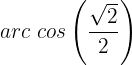 entspricht
entspricht
Nachhilfe in Mathe? Schau bei Superprof rein!
Grundlegende trigonometrische Identitäten
Trigonometrische Identitäten sind definierte Gleichungen, die uns helfen, algebraische Aufgaben zu lösen, ohne uns den Kopf zu zerbrechen
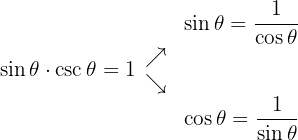
-
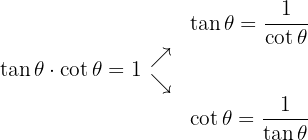
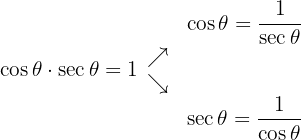
-
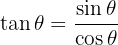
-
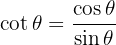
Pythagoreische trigonometrische Identitäten
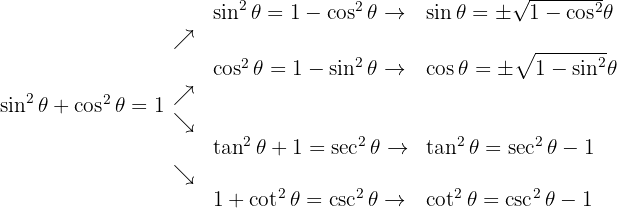
Gerade und ungerade trigonometrische Identitäten
Gerade Funktionen:
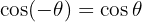
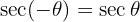
Ungerade Funktionen:
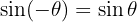
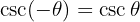
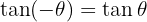
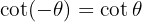
Doppelwinkel und Halbwinkel
Formel für Doppelwinkel:
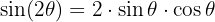
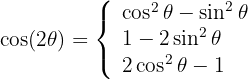
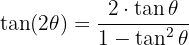
Formeln für Halbwinkel:
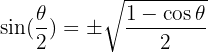
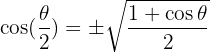
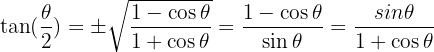
Addition und Subtraktion von Winkeln und Beziehungen zwischen Produkt und Summe
Trigonomische Identitäten der Summe und Differenz von Winkeln:
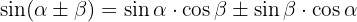
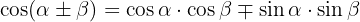
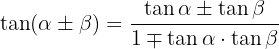
Trigonomische Identitäten Summe-Produkt:
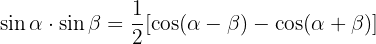
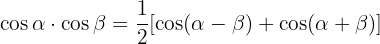
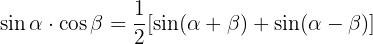
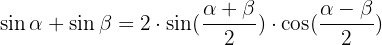
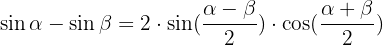
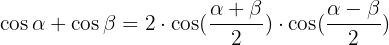
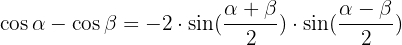
Aufgaben zu grundlegenden trigonometrischen Gleichungen
Löse, indem du die Variable ermittelst und die Werte auf dem Einheitskreis ausfindig machst.
1 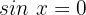
2 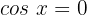
3 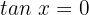
4 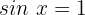
5 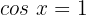
6 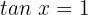
7 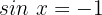
8 
9 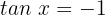
10 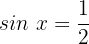
11 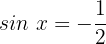
12 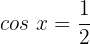
13 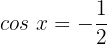
Um die folgenden trigonometrischen Gleichungen zu lösen, muss man sich die Eigenschaft der Umkehrfunktion vor Augen führen.:
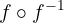 =x
=x
1 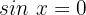
Wir ermitteln die Variable x unter Verwendung der Eigenschaft der Umkehrfunktion:
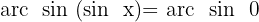
Wir suchen den Wert für 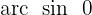 in der Tabelle
in der Tabelle
Wir sehen uns nun den Sinus, das heißt, die y-Achse an. Nun suchen wir den Wert 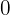 auf der Achse. Zum Schluss sehen wir uns die Punkte an, die den Kreis schneiden und durch
auf der Achse. Zum Schluss sehen wir uns die Punkte an, die den Kreis schneiden und durch 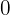 verlaufen. Diese Werte sind das Ergebnis der Gleichung.
verlaufen. Diese Werte sind das Ergebnis der Gleichung.
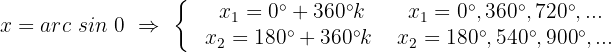

2 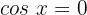
Wir ermitteln die Variable x unter Verwendung der Eigenschaft der Umkehrfunktion:
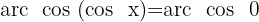
Wir suchen den Wert für 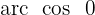 in der Tabelle
in der Tabelle
Wir sehen uns den cos an, das heißt, die x-Achse. Nun suchen wir den Wert 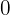 auf der Achse. Zum Schluss sehen wir uns die Punkte an, die den Kreis schneiden und durch
auf der Achse. Zum Schluss sehen wir uns die Punkte an, die den Kreis schneiden und durch 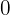 verlaufen. Diese Werte sind das Ergebnis der Gleichung
verlaufen. Diese Werte sind das Ergebnis der Gleichung
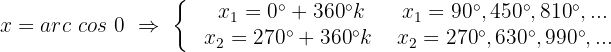
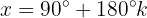
3 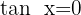
Wir ermitteln die Variable x unter Verwendung der Eigenschaft der Umkehrfunktion:
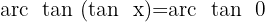
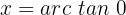
In unserer Tabelle visualisieren wir eine Tangente mit der Höhe 0. Wenn wir den Wert auf dem Einheitskreis suchen, stellen wir fest, dass er 0 Grad entspricht, also:

4 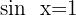
Wir ermitteln die Variable x unter Verwendung der Eigenschaft der Umkehrfunktion:
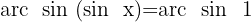
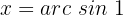
Wir suchen den Wert für 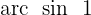 in der Tabelle
in der Tabelle
Wir sehen uns nun den Sinus, das heißt, die y-Achse an. Nun suchen wir den Wert 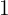 auf der Achse. Zum Schluss sehen wir uns die Punkte an, die den Kreis schneiden und durch
auf der Achse. Zum Schluss sehen wir uns die Punkte an, die den Kreis schneiden und durch 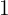 verlaufen. Diese Werte sind das Ergebnis der Gleichung.
verlaufen. Diese Werte sind das Ergebnis der Gleichung.

5 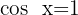
Wir ermitteln die Variable x unter Verwendung der Eigenschaft der Umkehrfunktion:
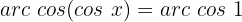
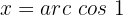
Wir suchen den Wert für 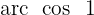 in der Tabelle
in der Tabelle
Wir sehen uns nun den cos, das heißt, die x-Achse an. Nun suchen wir den Wert 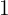 auf der Achse. Zum Schluss sehen wir uns die Punkte an, die den Kreis schneiden und durch
auf der Achse. Zum Schluss sehen wir uns die Punkte an, die den Kreis schneiden und durch 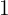 verlaufen. Diese Werte sind das Ergebnis der Gleichung
verlaufen. Diese Werte sind das Ergebnis der Gleichung

6 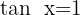
Wir ermitteln die Variable x unter Verwendung der Eigenschaft der Umkehrfunktion:
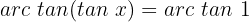
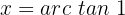
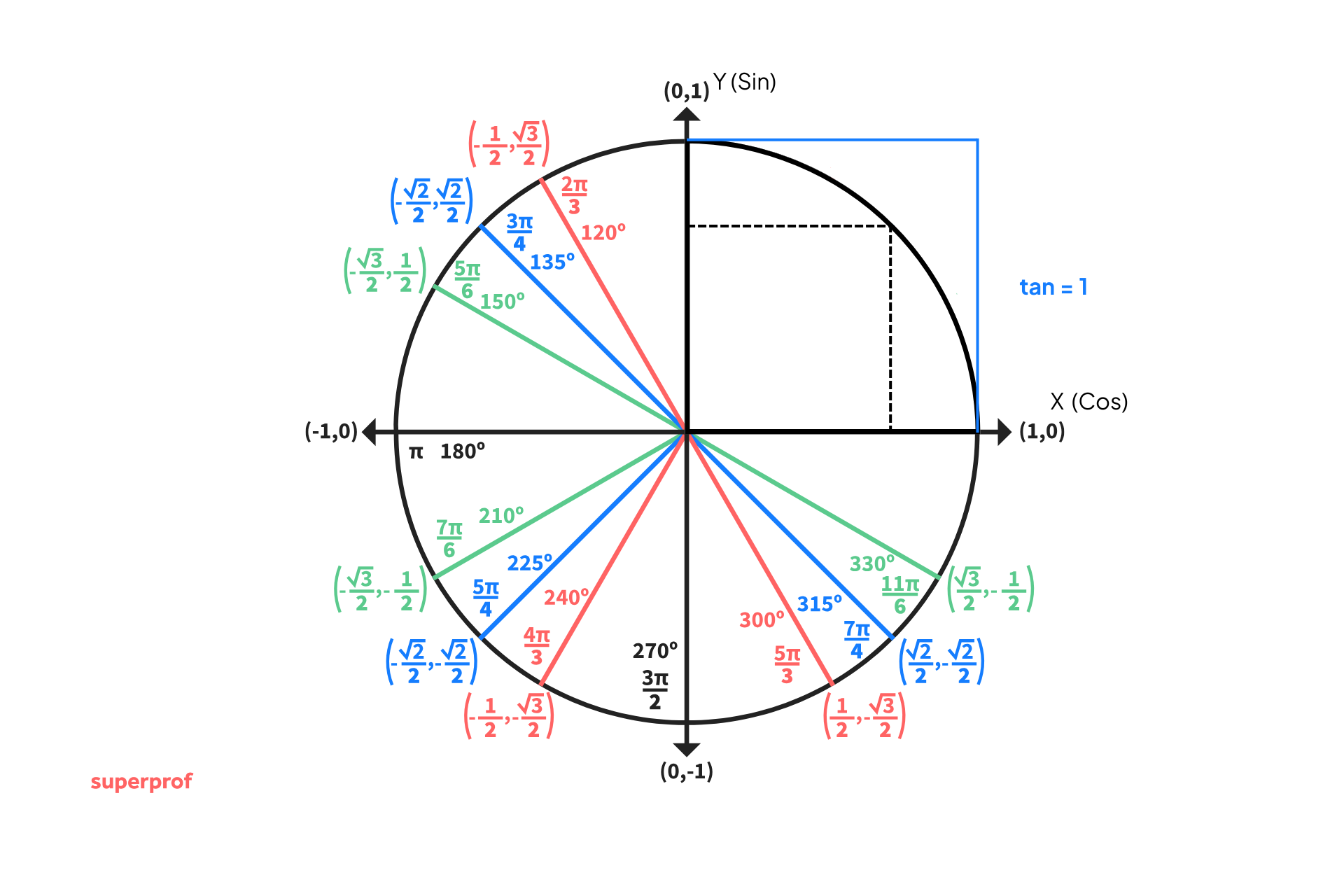
Diese Übung wurde im Beispiel zu Beginn der Lektion gezeigt, wo du die grafische Darstellung sehen kannst.
Wir visualisieren eine Tangente der Höhe  , zeichnen eine Linie von dieser Höhe bis zum Ursprung und betrachten den Schnittpunkt mit dem Kreis, suchen den Wert dieses Punktes auf unserem Einheitskreis und erhalten den Wert der Gleichung:
, zeichnen eine Linie von dieser Höhe bis zum Ursprung und betrachten den Schnittpunkt mit dem Kreis, suchen den Wert dieses Punktes auf unserem Einheitskreis und erhalten den Wert der Gleichung:

7 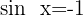
Wir ermitteln die Variable x unter Verwendung der Eigenschaft der Umkehrfunktion:
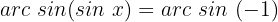
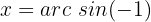
Wir suchen den Wert für 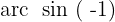 in der Tabelle
in der Tabelle
Wir sehen uns den sin an, das heißt, die y-Achse.Nun suchen wir den Wert  auf der Achse. Zum Schluss sehen wir uns die Punkte an, die den Kreis schneiden und durch
auf der Achse. Zum Schluss sehen wir uns die Punkte an, die den Kreis schneiden und durch  verlaufen. Diese Werte sind das Ergebnis der Gleichung
verlaufen. Diese Werte sind das Ergebnis der Gleichung
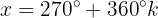
8 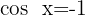
Wir ermitteln die Variable x unter Verwendung der Eigenschaft der Umkehrfunktion:
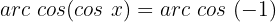

Wir suchen den Wert für 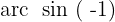 in der Tabelle
in der Tabelle
Nun sehen wir uns den cos an, das heißt, die x-Achse. Nun suchen wir den Wert  auf der Achse. Zum Schluss sehen wir uns die Punkte an, die den Kreis schneiden und durch
auf der Achse. Zum Schluss sehen wir uns die Punkte an, die den Kreis schneiden und durch  verlaufen. Diese Werte sind das Ergebnis der Gleichung
verlaufen. Diese Werte sind das Ergebnis der Gleichung

9 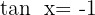
Wir ermitteln die Variable x unter Verwendung der Eigenschaft der Umkehrfunktion:
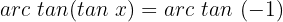
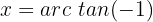
Nun sehen wir uns die Koordinate  an. Wir visualisieren eine Tangente der Höhe
an. Wir visualisieren eine Tangente der Höhe  , zeichnen eine Linie von dieser Höhe bis zum Ursprung und betrachten den Schnittpunkt mit dem Kreis. Wir suchen den Wert dieses Punktes auf unserem Einheitskreis und erhalten den Wert der Gleichung:
, zeichnen eine Linie von dieser Höhe bis zum Ursprung und betrachten den Schnittpunkt mit dem Kreis. Wir suchen den Wert dieses Punktes auf unserem Einheitskreis und erhalten den Wert der Gleichung:
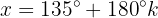
10 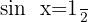
Wir ermitteln die Variable x unter Verwendung der Eigenschaft der Umkehrfunktion:
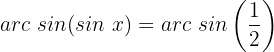
Wir suchen den Wert für 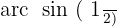 in der Tabelle
in der Tabelle
Wir sehen uns den sin an, das heißt, die y-Achse. Nun suchen wir den Wert  auf der Achse. Zum Schluss sehen wir uns die Punkte an, die den Kreis schneiden und durch
auf der Achse. Zum Schluss sehen wir uns die Punkte an, die den Kreis schneiden und durch verlaufen. Diese Werte sind das Ergebnis der Gleichung
verlaufen. Diese Werte sind das Ergebnis der Gleichung

11 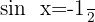
Wir ermitteln die Variable x unter Verwendung der Eigenschaft der Umkehrfunktion:
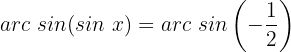
Wir suchen den Wert für 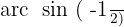 in der Tabelle
in der Tabelle
Wir sehen uns den sin an, das heißt, die y-Achse. Nun suchen wir den Wert 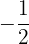 auf der Achse. Zum Schluss sehen wir uns die Punkte an, die den Kreis schneiden und durch
auf der Achse. Zum Schluss sehen wir uns die Punkte an, die den Kreis schneiden und durch 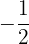 verlaufen. Diese Werte sind das Ergebnis der Gleichung
verlaufen. Diese Werte sind das Ergebnis der Gleichung
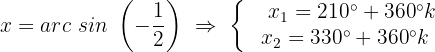
12 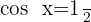
Wir ermitteln die Variable x unter Verwendung der Eigenschaft der Umkehrfunktion:
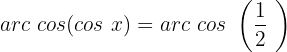
Wir suchen den Wert für 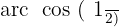 in der Tabelle
in der Tabelle
Wir sehen uns den cos an, das heißt, die x-Achse. Nun suchen wir den Wert  auf der Achse. Zum Schluss sehen wir uns die Punkte an, die den Kreis schneiden und durch
auf der Achse. Zum Schluss sehen wir uns die Punkte an, die den Kreis schneiden und durch  verlaufen. Diese Werte sind das Ergebnis der Gleichung
verlaufen. Diese Werte sind das Ergebnis der Gleichung

13 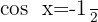
Wir ermitteln die Variable x unter Verwendung der Eigenschaft der Umkehrfunktion:

Wir suchen den Wert für 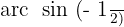 in der Tabellle
in der Tabellle
Wir sehen uns den sin an, das heißt, die y-Achse. Nun suchen wir den Wert 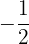 auf der Achse. Zum Schluss sehen wir uns die Punkte an, die den Kreis schneiden und durch
auf der Achse. Zum Schluss sehen wir uns die Punkte an, die den Kreis schneiden und durch 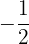 verlaufen. Diese Werte sind das Ergebnis der Gleichung
verlaufen. Diese Werte sind das Ergebnis der Gleichung

Löse unter Verwendung der trigonometrischen Identitäten
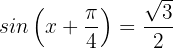
Um die Gleichung zu lösen, suchen wir in der Tabelle die Werte von 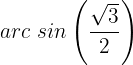
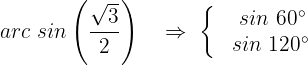
Wir erhalten 2 Fälle. Im ersten Fall setzen wir ein
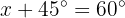
Wir ermitteln die Variable

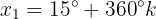
Wir setzen im zweiten Fall ein
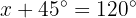
Wir ermitteln die Variable
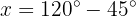
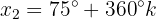
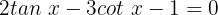
Mithilfe der trigonometrischen Identitäten versuchen wir, diese Gleichung in einfachere Funktionen wie Sinus, Kosinus oder Tangens zu vereinfachen.
Wir wenden die trigonometrische Identität 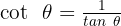 an
an
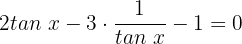
Wir wenden nun die trigonometrische Identität 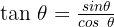 an
an
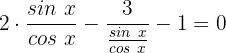
Wir vereinfachen:
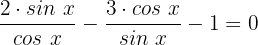
Wir subtrahieren die Brüche, indem wir das Kreuzprodukt anwenden und erhalten:
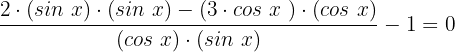
Wir vereinfachen:
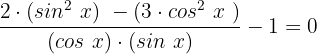
Wir wandeln die Einheit in einen äquivalenten Bruch mit dem gleichen Nenner um:
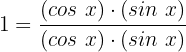
Wir setzen ein und vereinfachen
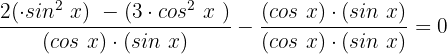
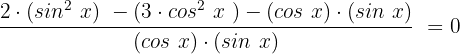
Nun multiplizieren wir beide Seiten der Gleichung mit 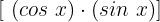
Auf der linken Seite erhalten wir :
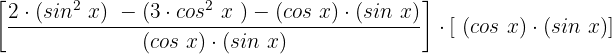
Wir vereinfachen und erhalten:
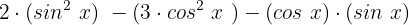
Auf der rechten Seite erhalten wir 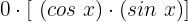 , was ganz klar gleich null ist
, was ganz klar gleich null ist
Und somit:
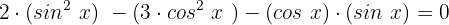
Wir faktorisieren:
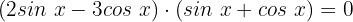
Nun gibt es 2 Fälle:
1. Fall: wir ermitteln den 1. Term
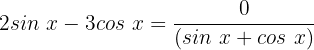
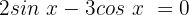
Für diesen Fall dividieren wir beide Glieder mit 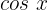
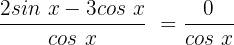
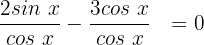
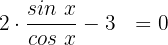
Wir wenden die Identität 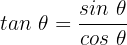 an
an
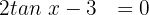
Wir ermitteln die Variable
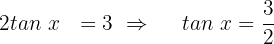
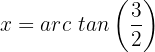
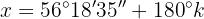
2. Fall: wir ermitteln den zweiten Term
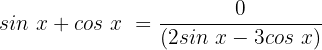
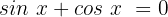
Für diesen Fall dividieren wir beide Glieder durch 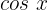
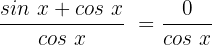
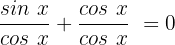
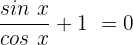
Wir wenden die Identität 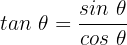 an
an
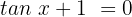
Wir ermitteln die Variable
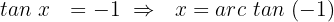
Nun suchen wir den Wert in unserem Einheitskreis, wie wir es zuvor getan haben

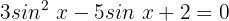
Wir können deutlich erkennen, dass die Gleichung die folgende Form hat:
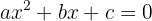
Das heißt, eine quadratische Gleichung, die mit der allgemeinen Formel gelöst werden kann:
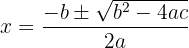
Wir setzen ein:
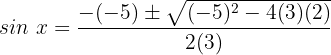
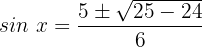
Fall 1:
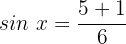
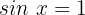
Wir ermitteln die Variable:
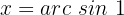
Wir suchen den Wert auf dem Einheitskreis
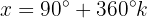
Fall 2:
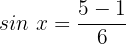
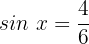
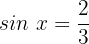
Wir ermitteln die Variable:
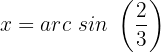
Wir suchen den Wert auf dem Einheitskreis
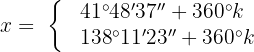
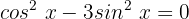
Wir wenden die folgende pythagoreische Identität an:
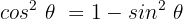
Wir setzen in unsere Gleichung ein:
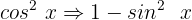
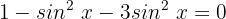
Wir addieren gleichartige Terme:
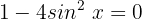
Wir ermitteln die Variable:
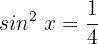
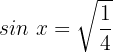
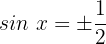

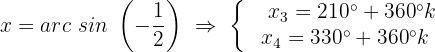
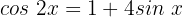
Wir wenden die trigonometrische Identität für Doppelwinkel an:
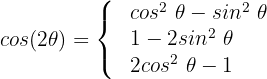
Von den drei Optionen, die wir haben, wenden wir die erste an: 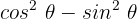
Wir setzen in unsere Gleichung ein:
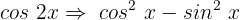
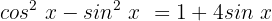
Nun wenden wir die folgende pythagoreische Identität an:
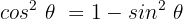
Wir setzen in unsere Gleichung ein:
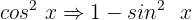
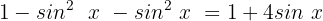
Wir setzen die Gleichung gleich 0 und vereinfachen die gleichartigen Terme
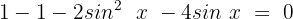
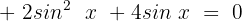
Nun faktorisieren wir:
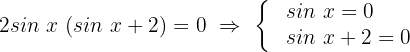
Wir stellen fest, dass zwei Fälle auftreten.
Fall 1:
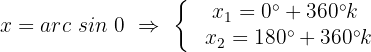

Fall 2:
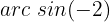
Wie wir am Einheitskreis sehen können, liegen die Werte der Sinus- und Kosinusfunktionen auf dem Intervall [-1,1], sodass 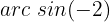 nicht existiert. Dieser Fall hat also keine Lösung.
nicht existiert. Dieser Fall hat also keine Lösung.
Ohne Lösung
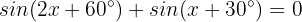
In diesem Fall wenden wir die trigonometrische Identität der Winkeladdition an:
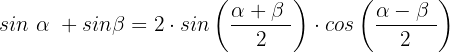
Wir setzen die Werte unserer Übung in die trigonometrische Identität ein:
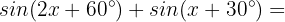
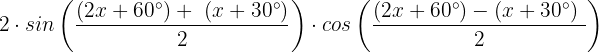
Wir vereinfachen gleichartige Terme:
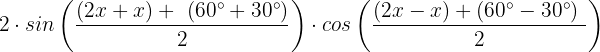
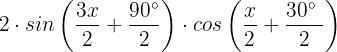
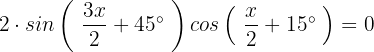
Damit die Gleichung gleich 0 ist, muss natürlich einer der beiden Terme gleich 0 sein:
Fall 1: 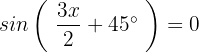
Fall 2: 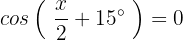
Wir lösen Fall 1:
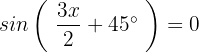
Wir ermitteln die Variable, indem wir die Umkehrfunktion anwenden:
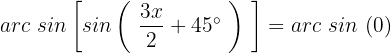
Wir sehen uns den Einheitskreis an und stellen fest:

Wir lösen die Gleichung nach 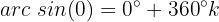 auf
auf
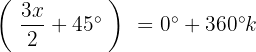
Wir bestimmen die Variable und lösen:
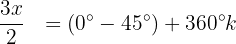
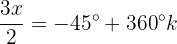
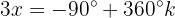
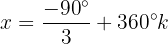

Wir lösen die Gleichung nach 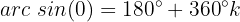 auf
auf
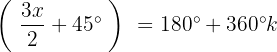
Wir bestimmen die Variable und lösen:
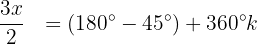

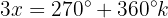
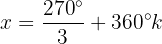
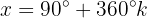
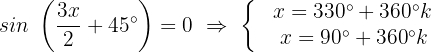
Dies bedeutet: Wenn die Variable x einen dieser 2 Werte annimmt, ist die Gleichung 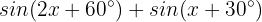 gleich 0.
gleich 0.
Wir lösen Fall 2:

Wir ermitteln die Variable, indem wir die Umkehrfunktion anwenden:
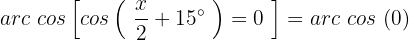
Wir sehen uns den Einheitskreis an und stellen fest:

Wir lösen die Gleichung nach 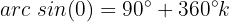 auf
auf

Wir bestimmen die Variable und lösen:
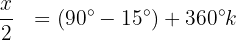


Wir lösen die Gleichung nach 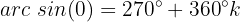 auf
auf
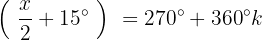
Wir bestimmen die Variable und lösen:
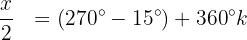
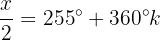

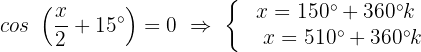
Dies bedeutet: Wenn die Variable x einen dieser 2 Werte annimmt, ist die Gleichung 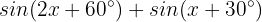 gleich 0.
gleich 0.
Zusammenfassend lässt sich sagen, dass die Werte, die die Variable x annehmen kann und die die Lösung der Gleichung sind, wie folgt lauten:

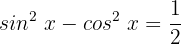
In diesem Fall wenden wir eine trigonometrische Identität für Doppelwinkel an:
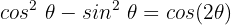
Zunächst multiplizieren wir unsere gesamte Gleichung mit -1 :
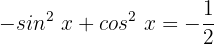
Jetzt ordnen wir das Ganze so an, dass es unserer trigonometrischen Identität ähnlicher wird
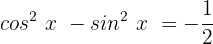
Wir wenden die Identität an, indem wir die Werte unserer Gleichung einsetzen :
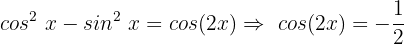
Um die Variable zu ermitteln, muss die Umkehrfunktion angewendet werden
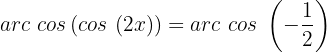

Wir suchen auf dem Einheitskreis und sehen, dass:
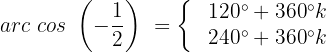
Wir lösen nach 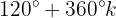 auf:
auf:
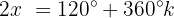
Wir ermitteln die Variable:

Wir lösen nach 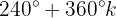 auf:
auf:
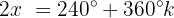
Wir ermitteln die Variable:
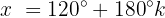
Die Werte, die die Variable x annehmen kann und die Lösung der Gleichung sind:

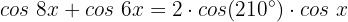
Wir wenden die trigonometrische Identität der Summe der Kosinusfunktionen an:
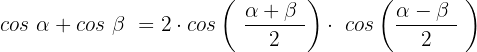
Wir setzen ein:
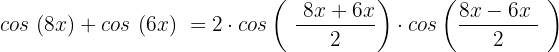

Unsere Gleichung sieht nun wie folgt aus:
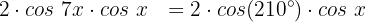
Wir teilen beide Seiten der Gleichung durch 2:
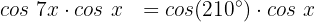
Wir teilen beide Seiten der Gleichung durch cos(x):
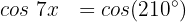
Wir wenden die Umkehrfunktion an:

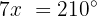
Wir ermitteln die Variable:

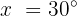
Die Gleichung ist erfüllt, wenn 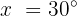
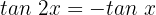
In diesem Fall wenden wir die trigonometrische Identität aus dem Abschnitt "Trigonometrische Identitäten für Doppelwinkel" an:
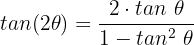
Wir setzen ein und erhalten:
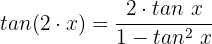
Unsere Gleichung sieht dann wie folgt aus:
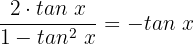
Wir setzen die Gleichung gleich 0:
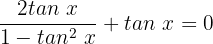
Wir addieren die Brüche mithilfe des Kreuzprodukts:
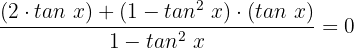
Wir eliminieren den Nenner, indem wir beide Seiten der Gleichung mit 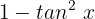 multiplizieren:
multiplizieren:
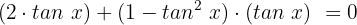
Wir multiplizieren:
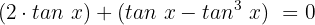
Wir fassen gleichartige Terme zusammen und addieren:
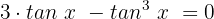
Wir faktorisieren mit 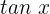 als gemeinsamen Faktor:
als gemeinsamen Faktor:

Nun dividieren wir beide Seiten der Gleichung durch 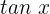 und erhalten:
und erhalten:
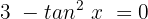
Wir multiplizieren beide Seiten der Gleichung mit -1 und lösen die Gleichung 2. Grades:
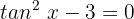
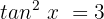
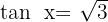
Wir wenden die Umkehrfunktion an:
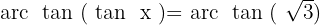
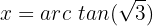
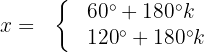
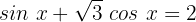
Zunächst subtrahieren wir  auf beiden Seiten:
auf beiden Seiten:
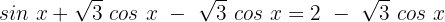
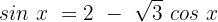
Wir quadrieren beide Seiten:
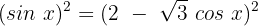
Wir setzen die Gleichung gleich 0:
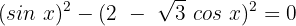
Wir lösen mit der Formel für ein Binom zum Quadrat:
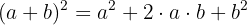
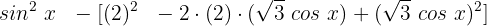
Wir wenden die trigonometrische Identität von Pythagoras an:
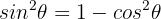
Wir setzen ein

Wir vereinfachen:


Wir vereinfachen gleichartige Terme:

Wir substituieren:
Sea 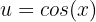
Wir setzen ein:
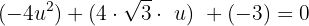
Es handelt sich um eine quadratische Gleichung, die wir mit der allgemeinen Formel lösen können:
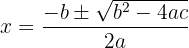
Wir setzen ein:
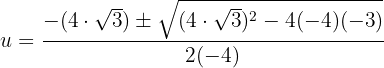
Wir lösen:
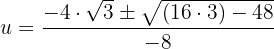

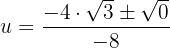
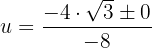
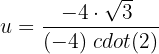

Wir machen die Substitution rückgängig:
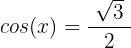
Wir wenden die Umkehrfunktion an:
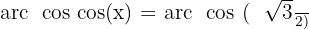

Jetzt müssen wir nur noch den Wert in unserer Einheitskreis-Tabelle finden:
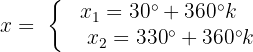
Die Gleichung ist erfüllt, wenn x einen dieser beiden Werte annimmt..
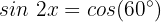
In diesem Fall wenden wir die trigonometrische Identität für Doppelwinkel an:
Wir suchen in unserem Einheitskreis den Wert, der 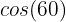 entspricht:
entspricht:

Wir setzen ein:
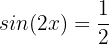
Wir wenden die Umkehrfunktion an:
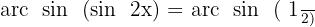
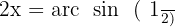
Wir suchen die entsprechenden Werte auf unserem Einheitskreis
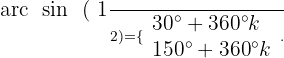
Somit:

Wir ermitteln die Variable, indem wir durch 2 teilen:
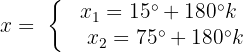
Die Gleichung ist erfüllt, wenn x einen dieser beiden Werte annimmt..
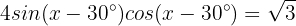
Wir wenden die folgende trigonometrische Identität für Doppelwinkel an:
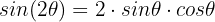
Bevor wir jedoch einsetzen, erhalten wir eine Variante, indem wir jede Seite der Identität durch 2 teilen:
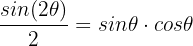
Wir setzen ein:
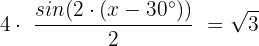
Wir vereinfachen, indem wir die angegebene Division durchführen:
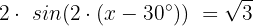
Wir teilen beide Seiten durch 2:
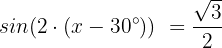
Wir wenden die Umkehrfunktion an:
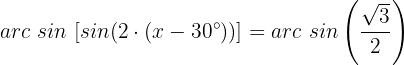
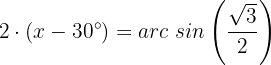
Wir suchen den Wert für 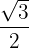 auf unserem Einheitskreis:
auf unserem Einheitskreis:

Wir setzen für beide Fälle ein:
Fall 1:
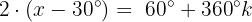
Wir teilen beide Seiten durch 2:
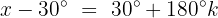
Wir ermitteln die Variable, indem wir beide Seiten der Gleichung mit 30° addieren:
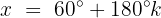
Fall 2:
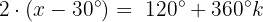
Wir teilen beide Seiten durch 2:
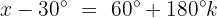
Wir ermitteln die Variable, indem wir beide Seiten der Gleichung mit 30° addieren:
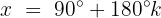
Die Gleichung ist erfüllt, wenn:
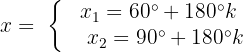
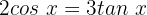
Wir wenden die grundlegende trigonometrische Identität an:
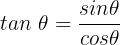
Wir setzen ein:
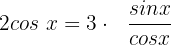
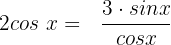
Wir eliminieren den Nenner, indem wir beide Seiten der Gleichung mit 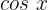 multiplizieren
multiplizieren
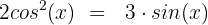
Jetzt wenden wir die trigonometrische Identität von Pythagoras an:
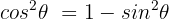
Wir setzen ein:
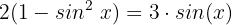
Wir wenden das Distributivgesetz an:
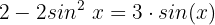
Wir setzen gleich 0 und ordnen:
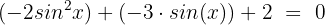
Wir multiplizieren den gesamten Ausdruck mit 
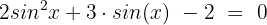
Wir substituieren, wobei:
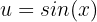
Wir setzen ein:

Wir lösen mit der Formel für quadratische Gleichungen:


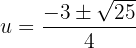

Wir machen die Substitution rückgängig:
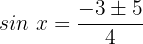
Fall 1:
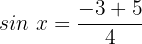
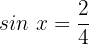
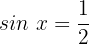
Wir wenden die Umkehrfunktion an:
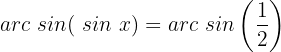
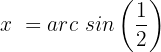
Wir suchen den entsprechenden Wert auf unserem Einheitskreis:
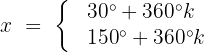
Fall 2:
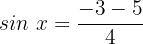
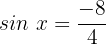
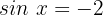
Wir wenden die Umkehrfunktion an:
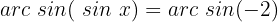
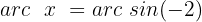
Wie wir wissen und auf unserem Einheitskreis beobachten können, ist die Sinusfunktion weder für Werte größer als 1 noch für Werte kleiner als -1 definiert, daher gibt es in diesem Fall keine Lösung.
Die Gleichung ist erfüllt, wenn:
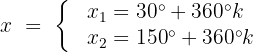
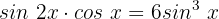
Wir wenden die folgende trigonometrische Identität für Doppelwinkel an:
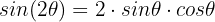
Wir setzen ein:
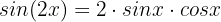
Somit:
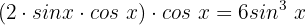
Wir vereinfachen:
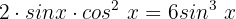
Wir setzen die Gleichung gleich 0:
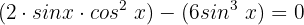
Wir faktorisieren:
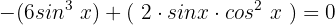
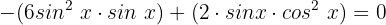
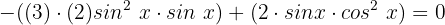
Wir extrahieren den gemeinsamen Term 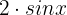 :
:
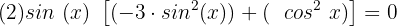
Nun faktorisieren wir den Teil in der eckigen Klammer :
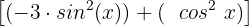
Wir schreiben die 3 als 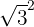
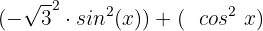
Wir ordnen, um die Differenz von Quadraten anwenden zu können:
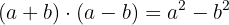
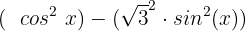
Wir wenden die Vorzeichenregel an  :
:
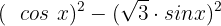
Nun berechnen wir wie folgt:
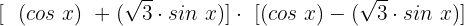
Zur Erinnerung: Dies ist das Ergebnis des Teils in Klammern oben. Wir setzen es nun in unsere Gleichung ein, nachdem wir sie faktorisiert haben:
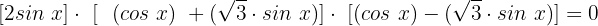
Es ist klar, dass es für die Erfüllung der Gleichung ausreicht, wenn nur eine der eckigen Klammern das Ergebnis 0 ergibt. Daher haben wir dann 3 Fälle:
Fall 1, wenn 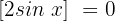
Wir teilen beide Glieder der Gleichung durch 2:
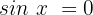
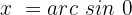
Wir suchen auf unserem Einheitskreis:
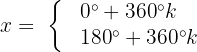
Fall 2, wenn 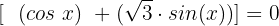
Wir dividieren beide Glieder durch cos x und wenden die grundlegende trigonometrische Identität des Tangens an:
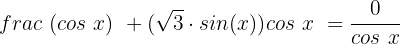
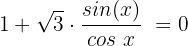
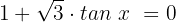
Wir ermitteln die Variable:
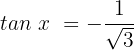
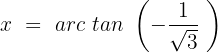

Fall 3, wenn 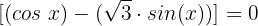
Dieser Fall ist dem Fall 2 sehr ähnlich:
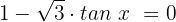
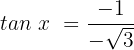
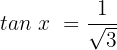
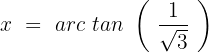

Die Gleichung ist erfüllt, wenn x einen der folgenden Werte annimmt:

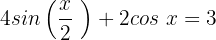
Wir setzen die Gleichung gleich 0:
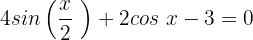
Wir substituieren, wobei 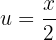
Wir setzen ein:
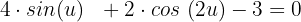
Wir wenden die folgende trigonometrische Identität für Doppelwinkel an:
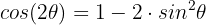
Wir setzen unsere Variable in die Identität ein:
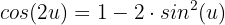
Wir setzen das Ergebnis in unsere Gleichung ein:
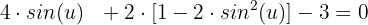
Wir berechnen:
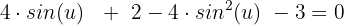
Wir addieren gleichartige Terme und ordnen:
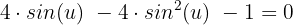
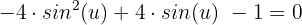
Wir substituieren erneut: 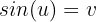
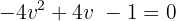
Wir lösen mit der Formel für quadratische Gleichungen:
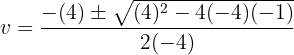

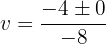
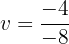
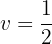
Wir machen die letzte Substitution rückgängig:
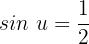
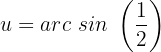
Wir suchen die Werte auf unserem Einheitskreis und erhalten:
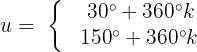
Nun machen wir die 1. Substitution rückgängig:
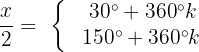
Wir ermitteln die Variable, indem wir mit 2 multiplizieren:
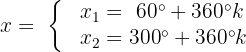
Die Gleichung ist erfüllt, wenn x einen dieser beiden Werte annimmt.
Mit KI zusammenfassen:












