Gegeben ist ein Dreieck mit:  ,
,  und
und  . Berechne die verbleibenden Elemente.
. Berechne die verbleibenden Elemente.
Gegeben ist ein Dreieck mit:  ,
,  und
und  . Berechne die verbleibenden Elemente.
. Berechne die verbleibenden Elemente.
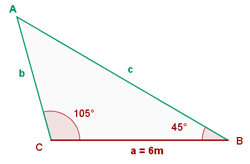
1 Da die Summe der drei Winkel 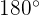 ist, können wir ganz einfach den Winkel
ist, können wir ganz einfach den Winkel  berechnen:
berechnen:

2 Wir wenden den Sinussatz an, um die Seiten  und
und  zu berechnen:
zu berechnen: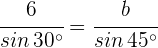
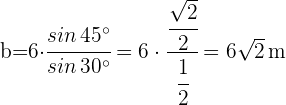
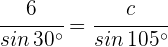
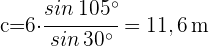
Gegeben ist ein Dreieck mit:  ,
,  und
und  . Berechne die verbleibenden Elemente.
. Berechne die verbleibenden Elemente.
Gegeben ist ein Dreieck mit:  ,
,  und
und  . Berechne die verbleibenden Elemente.
. Berechne die verbleibenden Elemente.
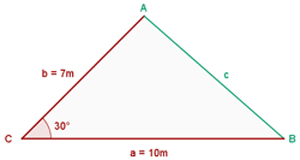
1 Wir wenden den Sinussatz an, um die Seite  zu berechnen:
zu berechnen:
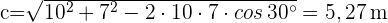
2 Wir wenden den Sinussatz an, um den Winkel  zu berechnen:
zu berechnen: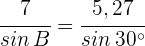
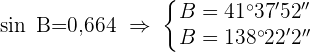
 , da
, da  ; der stumpfe Winkel ist
; der stumpfe Winkel ist  .
.
3 Um den Winkel  zu berechnen, überprüfen wir, ob die Summe
zu berechnen, überprüfen wir, ob die Summe  ist:
ist: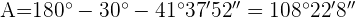
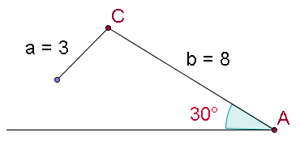
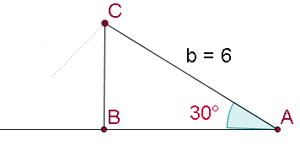
Löse das Dreieck mit den folgenden Werten: A = 30°, a = 3 m und b = 8 m.
Löse das Dreieck mit den folgenden Werten: 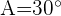 ,
, 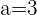 m und
m und 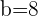 m.
m.
1 Wir wenden den Sinussatz mit den gegebenen Werten an
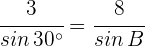
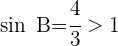
2 Da der Sinus eines Winkels nie größer als  sein kann, gibt es hierfür keine Lösung. Die Abbildung zeigt, dass solch ein Dreieck nicht existiert.
sein kann, gibt es hierfür keine Lösung. Die Abbildung zeigt, dass solch ein Dreieck nicht existiert.
Löse das Dreieck mit den folgenden Werten: 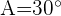 ,
, 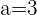 m und
m und 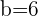 m.
m.
Löse das Dreieck mit den folgenden Werten: 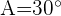 ,
, 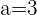 m und
m und 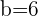 m.
m.
1Wir wenden den Sinussatz an, um den Winkel  zu berechnen:
zu berechnen:
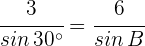
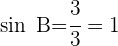
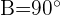
2 Da 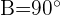 , ist das Dreieck rechtwinklig. Wir können den Winkel
, ist das Dreieck rechtwinklig. Wir können den Winkel  berechnen, da die spitzen Winkel
berechnen, da die spitzen Winkel  ergeben müssen:
ergeben müssen:
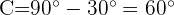
3 Wir berechnen die Seite  , indem wir Winkelfunktionen anwenden:
, indem wir Winkelfunktionen anwenden:

Löse das Dreieck mit den folgenden Werten: 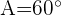 ,
,  m y
m y  m.
m.
Löse das Dreieck mit den folgenden Werten: 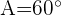 ,
,  m und
m und  m.
m.
1 Wir wenden den Sinussatz an, um den Winkel  zu berechnen
zu berechnen
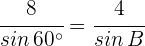
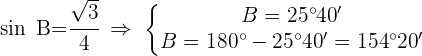
2 Da  , ist nur die folgende Lösung gültig:
, ist nur die folgende Lösung gültig: 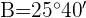
3 Wir berechnen den Winkel  , da die 3 Winkel
, da die 3 Winkel  ergeben müssen:
ergeben müssen:
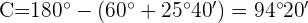
4 Wir berechnen die Seite  , indem wir den Sinussatz anwenden:
, indem wir den Sinussatz anwenden:
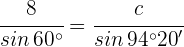
 m
m
Löse das Dreieck mit den folgenden Werten: 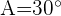 ,
,  und
und 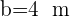 .
.
Löse das Dreieck mit den folgenden Werten: 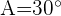 ,
,  und
und 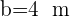 .
.
1 Wir wenden den Sinussatz an, um den Winkel  zu berechnen:
zu berechnen: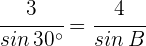
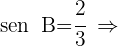

2 Da  sind die folgenden 2 Lösungen gültig
sind die folgenden 2 Lösungen gültig
3 Wir berechnen den Winkel  und die Seite
und die Seite  für den Wert von
für den Wert von 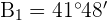
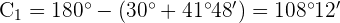
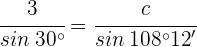
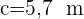
4 Wir berechnen den Winkel  und die Seite
und die Seite  für den Wert von
für den Wert von 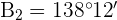
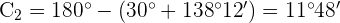
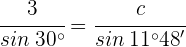
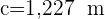
Löse das Dreieck mit den folgenden Werten:  ,
, 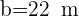 und
und 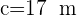 .
.
Löse das Dreieck mit den folgenden Werten:  ,
, 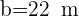 und
und 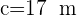 .
.
1 Wir wenden den Kosinussatz an, um die Winkel  und
und  zu berechnen
zu berechnen
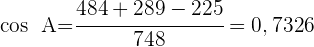
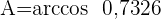
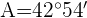
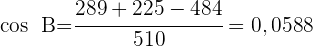
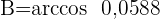

1 Wir berechnen den Winkel  unter der Annahme, dass die 3 Winkel
unter der Annahme, dass die 3 Winkel
 ergeben
ergeben
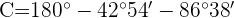
Berechne die Höhe  :
:
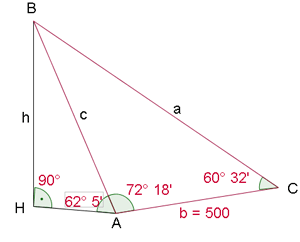
1 Da wir 2 Winkel des Dreiecks  kennen, können wir den Winkel
kennen, können wir den Winkel  berechnen, da die Summe der drei Winkel
berechnen, da die Summe der drei Winkel  sein muss
sein muss
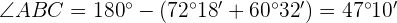
2 Wir wenden den Sinussatz an, um die Seite  zu berechnen:
zu berechnen:
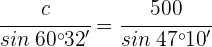
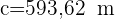
3 Da das Dreieck 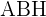 rechtwinklig ist, wenden wir Winkelfunktionen an, um die Seite
rechtwinklig ist, wenden wir Winkelfunktionen an, um die Seite  zu berechnen:
zu berechnen:
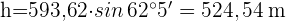
Berechne die Distanz, die zwischen  und
und  liegt.
liegt.
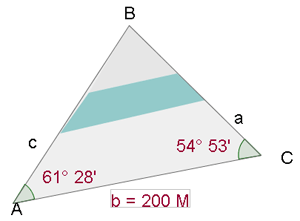
1 Wir sehen uns das Dreieck 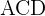 an und wenden den Sinussatz an, um
an und wenden den Sinussatz an, um  zu berechnen
zu berechnen
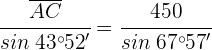
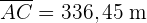
2 Wir sehen uns das Dreieck 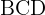 an und wenden den Sinussatz an, um
an und wenden den Sinussatz an, um  zu berechnen
zu berechnen
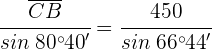

3 Wir wenden den Kosinussatz an, um die Distanz  zu berechnen
zu berechnen


Berechne die Distanz, die zwischen Punkt  und
und  liegt.
liegt.
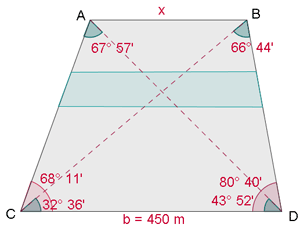
1 Wir sehen uns das Dreieck 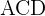 an und wenden den Sinussatz an, um
an und wenden den Sinussatz an, um  zu berechnen
zu berechnen
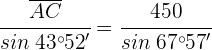
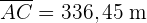
2 Wir sehen uns das Dreieck 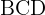 an und wenden den Sinussatz an, um
an und wenden den Sinussatz an, um  zu berechnen
zu berechnen
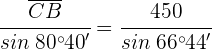

3 Wir wenden den Kosinussatz an, um die Distanz  zu berechnen
zu berechnen


Berechne den Radius des Umkreises des Dreiecks, wobei 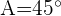 ,
, 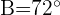 und
und 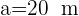 .
.
Berechne den Radius des Umkreises des Dreiecks, wobei 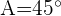 ,
, 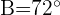 und
und 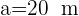 .
.
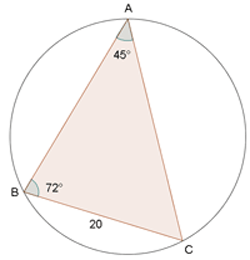
Es gilt 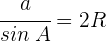
und somit 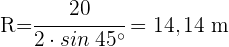
Der Radius eines Kreises misst  m. Berechne den Winkel, den die Tangenten mit dem Kreis bilden. Die Strecke vom Punkt A zum Punkt B misst
m. Berechne den Winkel, den die Tangenten mit dem Kreis bilden. Die Strecke vom Punkt A zum Punkt B misst  m.
m.
Der Radius eines Kreises misst  m. Berechne den Winkel, den die Tangenten mit dem Kreis bilden. Die Strecke vom Punkt A zum Punkt B misst
m. Berechne den Winkel, den die Tangenten mit dem Kreis bilden. Die Strecke vom Punkt A zum Punkt B misst  m.
m.
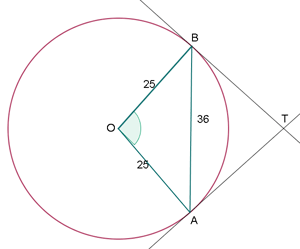
1 Wir wenden den Kosinussatz an, um den Winkel  zu berechnen
zu berechnen
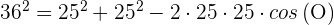

2 Im Viereck 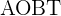 sind die Winkel
sind die Winkel  und
und  rechte Winkel.
rechte Winkel.
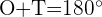

Die Diagonalen eines Parallelogramms sind  cm und
cm und  cm lang und der Winkel, den sie bilden, beträgt
cm lang und der Winkel, den sie bilden, beträgt  . Berechne die Seiten.
. Berechne die Seiten.
Die Diagonalen eines Parallelogramms sind  cm und
cm und  cm lang und der Winkel, den sie bilden, beträgt
cm lang und der Winkel, den sie bilden, beträgt  . Berechne die Seiten.
. Berechne die Seiten.
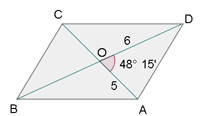
Wir berechnen 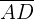 , indem wir den Kosinussatz anwenden
, indem wir den Kosinussatz anwenden
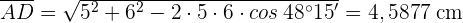
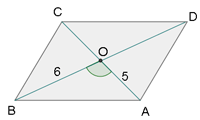
Wir berechnen den Winkel 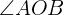 , da dieser supplementär zum Winkel
, da dieser supplementär zum Winkel 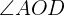 ist:
ist:

Wir wenden den Kosinussatz an, um  zu berechnen
zu berechnen
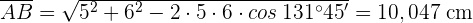
Dreiecke bereiten dir immer noch Kopfschmerzen? Unsere Matheprofis erklären dir alles zu diesem Thema und du kannst in deinem ganz eigenen Tempo lernen.
Mit KI zusammenfassen:



