
Was ist die Rationalisierung von Wurzeln?
Die Rationalisierung von Wurzeln besteht darin, die Wurzeln aus dem Nenner zu eliminieren, wodurch die Berechnung von Operationen wie der Addition von Brüchen erleichtert wird.
Wir unterscheiden drei Fälle:
Fall 1
Rationalisierung vom Typ 
Der Zähler und der Nenner werden mit 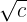 multipliziert.
multipliziert.
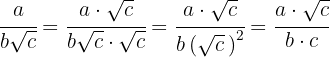
Beispiele
1 Rationalisiere den Ausdruck 
Wir multiplizieren den Zähler und den Nenner mit der Wurzel aus 2, führen die Berechnungen durch und vereinfachen den Bruch

2 Rationalisiere den Ausdruck 
Um die Addition durchführen zu können, rationalisieren wir den zweiten Summanden, indem wir ihn mit der Wurzel aus 2 multiplizieren und durch diese dividieren, und führen dann die Addition durch


Fall 2
Rationalisierung vom Typ 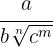
Der Zähler und der Nenner werden mit 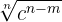 multipliziert.
multipliziert.

Beispiel
Rationalisiere den Ausdruck 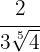
Wir schreiben den Radikanden  als Potenz:
als Potenz: 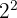
Wir müssen den Zähler und den Nenner mit der 5. Wurzel aus 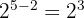 multiplizieren
multiplizieren
Wir multiplizieren die Wurzeln des Nenners, extrahieren Faktoren aus der Wurzel und vereinfachen den Bruch

Fall 3
Rationalisierung vom Typ 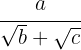
Und im Allgemeinen, wenn der Nenner ein Binom mit mindestens einer Wurzel ist.
Der Zähle rund der Nenner werden mit dem Konjugierten des Nenners multipliziert.
Das Konjugierte eines Binoms ist gleich dem Binom mit umgekehrtem Vorzeichen:

Wir müssen außerdem beachten: "Summe mal Differenz ist gleich".

Beispiele
1 Rationalisiere den Ausdruck 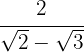
Wir multiplizieren den Zähler und den Nenner mit dem Konjugierten des Nenners, eliminieren die Klammern im Zähler und führen die Berechnung im Nenner durch. Wir erhalten
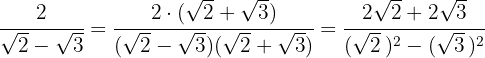
Im Nenner extrahieren wir die Radikanden und teilen durch  , das heißt, wir ändern das Vorzeichen im Zähler
, das heißt, wir ändern das Vorzeichen im Zähler
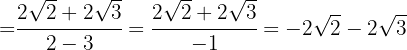
2 Rationalisiere den Ausdruck 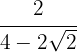
Wir mulitplizieren und dividieren den Nenner mit/durch das Konjugierte des Nenners

Wir berechnen die Summe mal Differenz im Nenner, führen die Berchnungen durch und vereinfachen den Bruch, indem wir durch  dividieren
dividieren
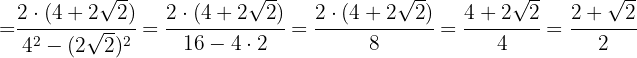
3 Rationalisiere den Ausdruck 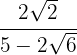
Wir multiplizieren den Nenner mit dem Konjugierten des Nenners, eliminieren die Klammern im Zähler und berechnen die Summe mal die Differenz im Nenner
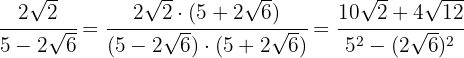
Im Zähler faktorisieren wir die  und extrahieren Faktoren. Zum Schluss führen wir die Berechnungen im Nenner durch
und extrahieren Faktoren. Zum Schluss führen wir die Berechnungen im Nenner durch

Beispielaufgaben
1
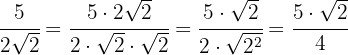
2
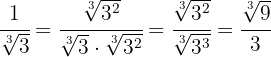
3
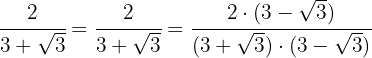
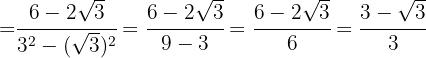
4
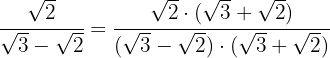

5
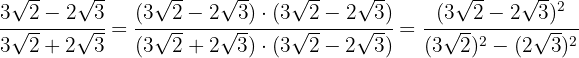
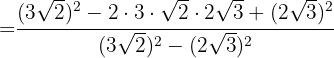
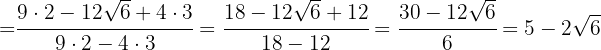
Mit KI zusammenfassen:












