Willkommen auf unserer Seite mit Aufgaben und Problemen, die mit dem Dreisatz gelöst werden! Der Dreisatz ist eines der praktischsten und nützlichsten Werkzeuge der Mathematik, um Verhältnisse zwischen verschiedenen Objekten zu bestimmen. Der Dreisatz ist wie ein Kompass, der uns durch Situationen führt, in denen wir Mengen in Beziehung setzen und genaue Proportionen finden müssen.
In diesem Bereich stellen wir dir verschiedene Übungen und Probleme vor, mit denen du deine Fähigkeiten in dieser Disziplin vertiefen kannst. Ganz gleich, ob du deine alltäglichen mathematischen Fähigkeiten verbessern oder den Dreisatz in komplexeren Zusammenhängen anwenden möchtest, hier bist du richtig – mach dich bereit, deinen Verstand herauszufordern und Dreisatz-Profi zu werden!
Zwei Räder sind durch einen Antriebsriemen verbunden. Das erste Rad hat einen Radius von  cm und das zweite von
cm und das zweite von  cm. Wenn das erste Rad
cm. Wenn das erste Rad  Umdrehungen zurückgelegt hat, wie viele Umdrehungen macht dann das zweite Rad?
Umdrehungen zurückgelegt hat, wie viele Umdrehungen macht dann das zweite Rad?
Zunächst einmal sind diese Größen umgekehrt proportional, denn je größer der Radius ist, desto weniger Umdrehungen macht es. Wenn  den Wert der gesuchten Umdrehungen darstellt, ergibt sich aus dem folgenden Diagramm, dass
den Wert der gesuchten Umdrehungen darstellt, ergibt sich aus dem folgenden Diagramm, dass
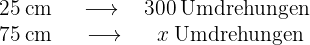
Der Anteil der Umdrehungen ist gleich dem Anteil des Radius
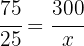
Somit ist der Wert von 
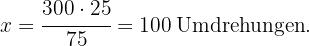
Der Maßstab auf einer Karte ist wie folgt:  cm auf der Karte entsprechen
cm auf der Karte entsprechen 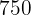 m in der Wirklichkeit. Wie viele Meter
m in der Wirklichkeit. Wie viele Meter  cm entsprechen in Wirklichkeit auf der Karte?
cm entsprechen in Wirklichkeit auf der Karte?
Zunächst einmal muss beachtet werden, dass es sich um direkt proportionale Größen handelt, d. h. je mehr Zentimeter auf der Karte, desto mehr Meter sind es im wirklichen Leben. Wenn also  die Anzahl der Meter in der Realität darstellt, dann ergibt sich aus dem folgenden Diagramm
die Anzahl der Meter in der Realität darstellt, dann ergibt sich aus dem folgenden Diagramm
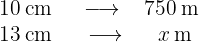
Das Verhältnis von Metern ist gleich dem Verhältnis von Zentimetern im folgenden Sinne
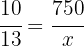
Somit ist der Wert von 

Sechs Personen können für  Tage in einem Hotel übernachten und zahlen dafür
Tage in einem Hotel übernachten und zahlen dafür 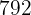 €. Wie viel kostet es für
€. Wie viel kostet es für  Personen, acht Tage in einem Hotel zu übernachten?
Personen, acht Tage in einem Hotel zu übernachten?
Je mehr Personen, desto höher die Kosten, und je mehr Tage, desto höher die Kosten, d. h. die Größenordnungen sind direkt proportional. Sei  der gesuchte Wert der Kosten, dann
der gesuchte Wert der Kosten, dann
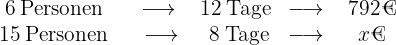
Daher ist der Anteil der Personen multipliziert mit dem Anteil der Tage gleich dem Anteil des Geldes, d.h.,
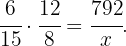
Nun ermitteln wir den Wert von 
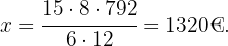
Somit kostet das Hotel für  für acht Tage
für acht Tage 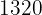 €.
€.
Ein Geschäft berechnet 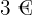 € für eine Geldsendung von
€ für eine Geldsendung von  €. Wenn der Betrag nicht genau ist, wird der entsprechende Betrag berechnet. Wenn eine Person
€. Wenn der Betrag nicht genau ist, wird der entsprechende Betrag berechnet. Wenn eine Person  € hinterlegt, wieviel berechnet dann das Geschäft für die Geldsendung?
€ hinterlegt, wieviel berechnet dann das Geschäft für die Geldsendung?
Zunächst einmal handelt es sich um direkt proportionale Größenordnungen, denn je mehr Geld gesendet wird, umso mehr wird berechnet. Wenn also  für den Betrag steht, der für das Senden des Geldes berechnet wird, ergibt sich aus dem folgenden Diagramm Folgendes
für den Betrag steht, der für das Senden des Geldes berechnet wird, ergibt sich aus dem folgenden Diagramm Folgendes

Das Verhältnis des berechneten Betrages ist gleich dem Verhältnis des gesendeten Betrages in folgendem Sinne
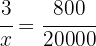
Somit ist der Wert von 
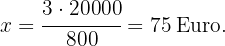
Wenn  Dosen mit jeweils
Dosen mit jeweils 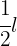 Farbe verwendet werden, um
Farbe verwendet werden, um  m eines
m eines  cm hohen Zaunes zu streichen: Berechne, wie viele
cm hohen Zaunes zu streichen: Berechne, wie viele  Dosen Farbe benötigt werden, um einen ähnlichen Zaun von
Dosen Farbe benötigt werden, um einen ähnlichen Zaun von  cm Höhe und
cm Höhe und  Metern Länge zu streichen.
Metern Länge zu streichen.
Je mehr Farbe in einem Behälter ist, desto weniger Behälter brauchen wir. Die Größenordnungen sind umgekehrt proportional. Je mehr Fläche wir zu streichen haben, desto mehr Behälter brauchen wir. Es handelt sich um direkt proportionale Größen und diese Information ermöglicht es uns, das folgende Diagramm zu erstellen
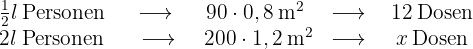
In diesem Fall ist  die Anzahl der Farbdosen, die wir benötigen. In der mittleren Spalte des Diagramms haben wir die Länge des Zauns in Meter umgerechnet und die Fläche des Zauns berechnet, indem wir die Höhe mit der Länge multipliziert haben.
die Anzahl der Farbdosen, die wir benötigen. In der mittleren Spalte des Diagramms haben wir die Länge des Zauns in Meter umgerechnet und die Fläche des Zauns berechnet, indem wir die Höhe mit der Länge multipliziert haben.
Nun bestimmen wir den Wert von  in der folgenden Gleichung
in der folgenden Gleichung
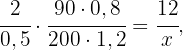
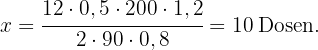
Es dauert  Tage mit
Tage mit  Arbeitern, um ein Haus zu bauen. Wie viele Tage würde es dauern, wenn
Arbeitern, um ein Haus zu bauen. Wie viele Tage würde es dauern, wenn  zusätzliche Arbeiter zur Verfügung stehen würden?
zusätzliche Arbeiter zur Verfügung stehen würden?
Zunächst ist zu beachten, dass die Variable Arbeiter umgekehrt zur Variable Tage ist, denn es liegt auf der Hand, dass der Bau des Hauses umso weniger Zeit in Anspruch nimmt, je mehr Arbeiter arbeiten. Wenn also  den gesuchten Wert der Tage darstellt, ergibt sich aus dem folgenden Diagramm, dass
den gesuchten Wert der Tage darstellt, ergibt sich aus dem folgenden Diagramm, dass
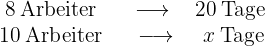
Das Verhältnis zwischen der Zahl der Arbeitskräfte und der Zahl der Tage ist in folgendem Sinne invers
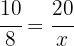
Somit ist der Wert von 
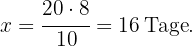
 Arbeiter pflügen ein rechteckiges Feld von
Arbeiter pflügen ein rechteckiges Feld von 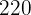 m Länge und
m Länge und  m Breite in
m Breite in  Tagen. Wie viele Arbeiter werden benötigt, um ein ähnliches Feld von
Tagen. Wie viele Arbeiter werden benötigt, um ein ähnliches Feld von  m Länge und
m Länge und 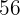 m Breite in fünf Tagen zu pflügen?
m Breite in fünf Tagen zu pflügen?
Je größer die Fläche, desto mehr Tage werden benötigt. Die Größenordnungen sind direkt proportional. Je mehr Tage, desto weniger Arbeiter werden benötigt. Diese Größen sind umgekehrt proportional. Daraus ergibt sich das folgende Diagramm
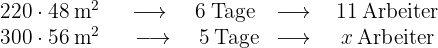
In dem Diagrammansatz in der ersten Spalte haben wir die Fläche des Feldes berechnet, indem wir die Breite mit der Länge multipliziert haben. Nun müssen wir den Wert von  aus der folgenden Gleichung ermitteln
aus der folgenden Gleichung ermitteln

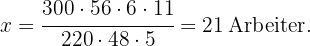
Das bedeutet, dass  Arbeiter benötigt werden, um das Feld von
Arbeiter benötigt werden, um das Feld von  m Länge und
m Länge und  m Breite in fünf Tagen zu pflügen.
m Breite in fünf Tagen zu pflügen.
 Pflegekräfte versorgen
Pflegekräfte versorgen  Patienten in
Patienten in  Tagen. Wieviele Pflegekräfte werden benötigt, um
Tagen. Wieviele Pflegekräfte werden benötigt, um  Patienten in
Patienten in  Tagen zu versorgen?
Tagen zu versorgen?
Erstens: Je mehr Pflegekräfte, desto weniger Tage werden für die Betreuung der Patienten benötigt, also ist die Variable Tage invers. Ebenso gilt: Je mehr Patienten, desto mehr Pflegekräfte werden benötigt, also ist die Variable Patienten direkt proportional. Wenn also  die Anzahl der gesuchten Pflegekräfte ist, kann das Problem wie folgt dargestellt werden:
die Anzahl der gesuchten Pflegekräfte ist, kann das Problem wie folgt dargestellt werden:
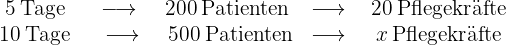
Daher ist der inverse Anteil der Tage multipliziert mit dem Anteil der Patienten gleich dem Anteil der Pflegekräfte, da die Variable Tage umgekehrt und die Variable Patienten direkt proportional ist, d. h,
Wir bestimmen nun den Wert von 
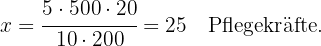
Sechs Wasserhähne benötigen  Stunden, um einen Tank mit einem Fassungsvermögen von
Stunden, um einen Tank mit einem Fassungsvermögen von  zu befüllen. Wie viele Stunden benötigen vier Wasserhähne, um
zu befüllen. Wie viele Stunden benötigen vier Wasserhähne, um  Tanks mit je
Tanks mit je  zu füllen?
zu füllen?
Je mehr Wasserhähne, desto weniger Stunden. Es handelt sich um umgekehrt proportionale Größen. Je mehr Tanks, desto mehr Stunden. Es handelt sich um direkt proportionale Größen. Je mehr 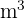 , desto mehr Stunden. Es handelt sich um direkt proportionale Größen. Mit diesen Informationen können wir das folgende Diagramm erstellen
, desto mehr Stunden. Es handelt sich um direkt proportionale Größen. Mit diesen Informationen können wir das folgende Diagramm erstellen 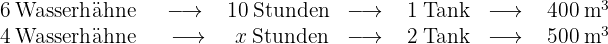 Diese
Diese  Mengen stehen in folgendem Verhältnis:
Mengen stehen in folgendem Verhältnis: 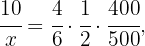 . Wenn wir den Wert von
. Wenn wir den Wert von  Stunden bestimmen, erhalten wir
Stunden bestimmen, erhalten wir 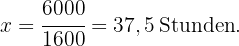 Vier Wasserhähne benötigen also
Vier Wasserhähne benötigen also 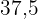 Stunden, um
Stunden, um  Tanks mit
Tanks mit  zu befüllen.
zu befüllen.
 Nähmaschinen haben gestern
Nähmaschinen haben gestern  Kleidungsstücke hergestellt. Wenn heute nur
Kleidungsstücke hergestellt. Wenn heute nur  Maschinen zur Verfügung stehen, wie viele Kleidungsstücke werden sie dann heute herstellen?
Maschinen zur Verfügung stehen, wie viele Kleidungsstücke werden sie dann heute herstellen?
Dabei ist zu beachten, dass es sich bei der Variable "Maschine" um eine direkt proportionale Variable handelt, d. h. wenn weniger Maschinen vorhanden sind, werden auch weniger Kleidungsstücke hergestellt. Wenn also  die Anzahl der gesuchten Kleidungsstücke darstellt, ergibt sich aus dem folgenden Diagramm Folgendes
die Anzahl der gesuchten Kleidungsstücke darstellt, ergibt sich aus dem folgenden Diagramm Folgendes
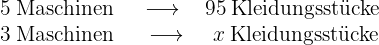
Daher ist das Verhältnis der Maschinen gleich dem Verhältnis der Kleidungsstücke in folgendem Sinne
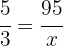
Der Wert von x ist also
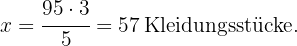
Mit KI zusammenfassen:



Ich habe den Kettensatz mit seinerzeit in der Handelsakademie gelernt . Er wurde vertikal angeordnet, was sehr übersichtlich war und man konnte es kaum verfehlen, die „richtigen“ Glieder zu verknüpfen. Ich erinnere mich nicht mehr genau daran, aber oft waren es auch 20 „Glieder“ in der vertikalen Anordnung. Ich fand diese Anschreibung viel einfacher.