
Einführung in die proportionale Zuordnung
In der Mathematik werden zwei Arten von Zuordnungen unterscheiden, um das Verhältnis zwischen zwei Werten darzustellen:
1. die proportionale Zuordnung: nach dem Schema "je mehr, desto mehr"
2. die antiproportionale Zuordnung: nach dem Schema "je mehr, desto weniger"
Für die visuelle Darstellung von Zuordnungen verwendet man die Schreibweise mit Pfeildiagrammen.
Gemischte Aufgaben

In einer Zuordnung ist das Produkt der Mittelwerte gleich dem Produkt der Extremwerte


In einer Zuordnung ist das Produkt der Mittelwerte gleich dem Produkt der Extremwerte
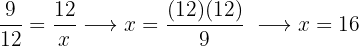
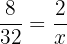
In einer Zuordnung ist das Produkt der Mittelwerte gleich dem Produkt der Extremwerte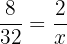
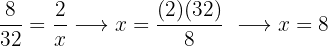
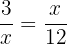
In einer Zuordnung ist das Produkt der Mittelwerte gleich dem Produkt der Extremwerte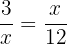
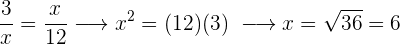

In einer Zuordnung ist das Produkt der Mittelwerte gleich dem Produkt der Extremwerte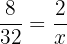
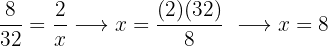
Rechenaufgabe: Umdrehungen
Zwei Räder sind durch einen Antriebsriemen miteinander verbunden. Das erste Rad hat einen Radius von 25 cm, das zweite von 75 cm. Wie oft hat sich das zweite Rad gedreht, wenn das erste 300 Umdrehungen realisiert hat?
Es handelt sich hier um eine antiproportionale Zuordnung, da die Umdrehungen der Räder geringer sind, je größer ihr Radius ist.
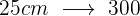 Umdrehungen
Umdrehungen
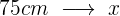 Umdrehungen
Umdrehungen
Folgende Formel gilt für die antiproportionale Zuordnung
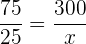
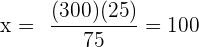 Umdrehungen
Umdrehungen
Rechenaufgabe: Hotelkosten
Der Aufenthalt für sechs Personen in einem Hotel kostet 792 € für 12 Tage. Wie viel kostet der Aufenthalt für 15 Personen und 8 Tage?
Je mehr Personen im Hotel unterkommen, desto mehr kostet der Aufenthalt. Es handelt sich hier also um eine proportionale Zuordnung.
Je mehr Personen im Hotel unterkommen, desto mehr kostet der Aufenthalt. Es handelt sich hier also um eine proportionale Zuordnung.
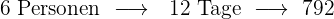 €
€
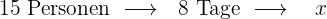 €
€
Folgende Formel gilt für die proportionale Zuordnung
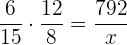
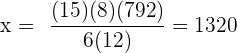 €
€
Rechenaufgabe: Farbeimer
Wenn man mit 12 Eimern à  Farbe einen 90m langen und
Farbe einen 90m langen und
80 cm hohen Zaun streichen kann, wie viele Eimer à 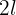 Farbe würde man benötigen,
Farbe würde man benötigen,
wenn man einen ähnlichen Zaun mit  Höhe und
Höhe und  Länge streichen wollte?
Länge streichen wollte?
Je mehr Kilo Farbe benötigt wird, desto weniger Eimer, das heißt, es liegt eine antiproportionale Zuordnung vor.
Je mehr 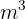 man streichen will, desto mehr Farbeimer benötigt man, das heißt, es liegt außerdem eine proportionale Zuordnung vor.
man streichen will, desto mehr Farbeimer benötigt man, das heißt, es liegt außerdem eine proportionale Zuordnung vor.
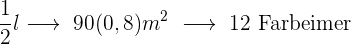

Folgende Formel gilt für die Zuordnung
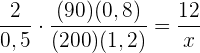
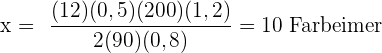
Rechenaufgabe: Bauarbeiter
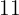 Bauarbeiter bearbeiten eine rechteckige Fläche von
Bauarbeiter bearbeiten eine rechteckige Fläche von  Länge und
Länge und 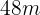 Breite
Breite 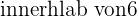 Tagen. Wie viele Bauarbeiter wären nötig, um eine ähnlich beschaffenes Fläche mit
Tagen. Wie viele Bauarbeiter wären nötig, um eine ähnlich beschaffenes Fläche mit 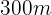 Länge und
Länge und  Breite in 5 Tagen zu bearbeiten?
Breite in 5 Tagen zu bearbeiten?
Je mehr Fläche, desto mehr Bauarbeiter werden benötigt, das heißt, es liegt eine proportionale Zuordnung
Je mehr Tage man zur Verfügung hat, desto weniger Bauarbeiter benötigt man, das heißt, es liegt außerdem eine antiproportionale Zuordnung vor
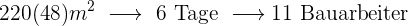
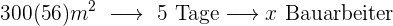
Folgende Formel gilt für die Zuordnung
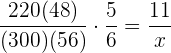
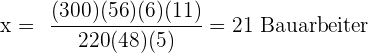
Rechenaufgabe: Wassertank
Man benötigt 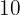 Stunden, um einen Wassertank mit einer Kapazität von
Stunden, um einen Wassertank mit einer Kapazität von 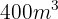 mithilfe von sechs Wasserschläuchen zu befüllen. Wie viele Stunden würde man benötigen, um
mithilfe von sechs Wasserschläuchen zu befüllen. Wie viele Stunden würde man benötigen, um 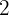 Wassertanks mit einer Kapazität von jeweils
Wassertanks mit einer Kapazität von jeweils 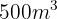 mithilfe von vier Wasserschläuchen zu befüllen?
mithilfe von vier Wasserschläuchen zu befüllen?
Je mehr Wasserschläuche, desto weniger Stunden benötigt man, das heißt, es liegt eine proportionale Zuordnung vor.
Je größer der Tank, desto mehr Stunden benötigt man, das heißt, es liegt eine weitere proportionale Zuordnung vor.
Je mehr 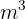 Volumen der Tank aufweist, desto mehr Stunden benötigt man, das heißt, es liegt eine weitere proportionale Zuordnung vor.
Volumen der Tank aufweist, desto mehr Stunden benötigt man, das heißt, es liegt eine weitere proportionale Zuordnung vor.
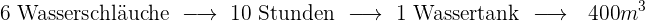
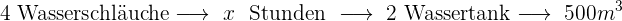
Folgende Formel gilt für die Zuordnung
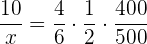
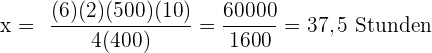
Rechenaufgabe: Schüler
Von den  Schülern eines Gymnasiums sind
Schülern eines Gymnasiums sind 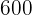 auf einem Schulausflug.
auf einem Schulausflug.
Wie viel Prozent der Schüler sind auf einem Schulausflug?
Es handelt sich um eine proportionale Zuordnung:
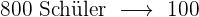 %
%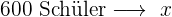
Folgende Formel gilt für die Zuordnung
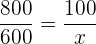
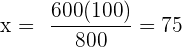 %
%
Rechenaufgabe: Rabatt beim Autokauf
Beim Kauf eines Fahrzeugs mit einem Preis von 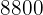 € erhalten wir einen Rabatt von
€ erhalten wir einen Rabatt von 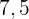 %. Wie viel müssen wir für das Fahrzeug bezahlen?
%. Wie viel müssen wir für das Fahrzeug bezahlen?
Beginne mit der Zuordnung wie folgt:  €
€ 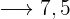 €
€
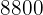 €
€ 
Folgende Formel gilt für die Zuordnung
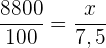
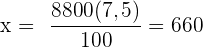 €
€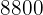 € -
€ -  €
€ 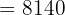 €
€
Die Aufgabe kann auch auf eine direktere Weise berechnet werden:
Es liegt ein Rabatt von 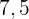 %, vor, das heißt, je
%, vor, das heißt, je  € bezahlt man
€ bezahlt man 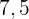 € weniger. Anstelle von
€ weniger. Anstelle von  € bezahlen wir also
€ bezahlen wir also 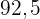 €.
€.
 €
€ 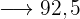 €
€
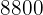 €
€ 
Folgende Formel gilt für die Zuordnung
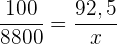
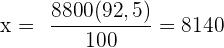 €
€
Rechenaufgabe: Mehrwertsteuer beim Computerkauf
Ein Computer kostet  € (zzgl. Mehrwertsteuer). Wie viel muss man insgesamt bezahlen, wenn die Mehrwertsteuer
€ (zzgl. Mehrwertsteuer). Wie viel muss man insgesamt bezahlen, wenn die Mehrwertsteuer  % beträgt?
% beträgt?
Die Mehrwertsteuer liegt bei  %, das heißt, je
%, das heißt, je  € bezahlt man
€ bezahlt man 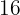 mehr. Anstelle von
mehr. Anstelle von  € bezahlt man also
€ bezahlt man also 
 €
€  €
€
 €
€  €
€
Folgende Formel gilt für die Zuordnung
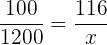
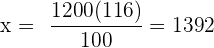 €
€
Rechenaufgabe: Rabatt beim Kauf eines Monitors
Beim Kauf eines Monitors mit einem Preis von  € erhalten wir einen Rabatt von
€ erhalten wir einen Rabatt von 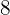 . Wie viel müssen wir bezahlen?
. Wie viel müssen wir bezahlen?
Wir erhalten einen Rabatt von 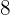 %, das heißt, je
%, das heißt, je  € bezahlen wir
€ bezahlen wir 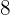 € weniger. Anstelle von
€ weniger. Anstelle von  € bezahlen wir also nur
€ bezahlen wir also nur  €.
€.
Lösung:
 €
€ 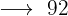 €
€
 €
€ 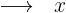
Folgende Formel gilt für die Zuordnung
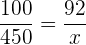
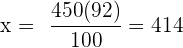 €
€
Rechenaufgabe: Gewinn im Verkauf
Ein Warenhaus verkauft einen Artikel mit 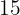 % Gewinn im Vergleich zum Einkaufspreis. Der Einkaufspreis betrug
% Gewinn im Vergleich zum Einkaufspreis. Der Einkaufspreis betrug 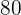 €. Ermittle den Verkaufspreis.
€. Ermittle den Verkaufspreis.
Der gewünschte Gewinn liegt bei 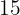 % im Vergleich zum Einkaufspreis, das heißt,
% im Vergleich zum Einkaufspreis, das heißt,
je  € muss der Endkäufer also
€ muss der Endkäufer also 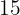 € mehr bezahlen. Anstelle von
€ mehr bezahlen. Anstelle von  € muss er
€ muss er 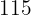 € bezahlen.
€ bezahlen.
 €
€  €
€
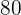 €
€ 
Folgende Formel gilt für die Zuordnung
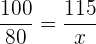
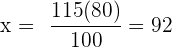 €
€
Rechenaufgabe I: Verkauf eines Artikels
Welcher Verkaufspreis muss auf dem Preisschild eines Artikels stehen, der im Einkauf 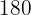 € gekostet hat, um im Verkauf
€ gekostet hat, um im Verkauf 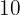 % Gewinn zu machen?
% Gewinn zu machen?
Wenn der Einkaufspreis bei  € liegt und
€ liegt und 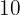 % Gewinn erzielt werden sollen, muss der Verkaufspreis bei
% Gewinn erzielt werden sollen, muss der Verkaufspreis bei 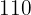 € liegen.
€ liegen.
Verkauf Einkauf
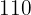 €
€ 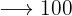 €
€
 €
€
Folgende Formel gilt für die Zuordnung

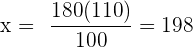 €
€
Rechenaufgabe II: Verkauf eines Artikels
Ein Artikel wurde im Einkauf für  € erhalten und mit
€ erhalten und mit 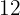 % Verlust verkauft. Welcher Preis steht auf seinem Verkaufsschild?
% Verlust verkauft. Welcher Preis steht auf seinem Verkaufsschild?
Wenn der Verkaufspreis bei  € liegt und man
€ liegt und man 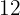 % Verlust macht, lag der Einkaufspreis bei
% Verlust macht, lag der Einkaufspreis bei  €.
€.
Verkauf Einkauf
 €
€ 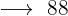
 €
€ 
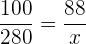
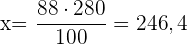 €
€
Rechenaufgabe III: Verkauf eines Artikels
Beim Verkauf eines Objekts werden 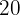 % Verlust im Vergleich zum Einkaufspreis gemacht. Zu welchem Preis wird das Objekt verkauft, wenn der Einkaufspreis
% Verlust im Vergleich zum Einkaufspreis gemacht. Zu welchem Preis wird das Objekt verkauft, wenn der Einkaufspreis 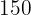 € betrug.
€ betrug.
Wenn der Einkaufspreis bei  € liegt und man
€ liegt und man 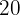 % Verlust macht, liegt der Verkaufspreis bei
% Verlust macht, liegt der Verkaufspreis bei 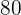 €.
€.
Einkauf Verkauf
 €
€ 
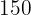 €
€ 
Folgende Formel gilt für die Zuordnung
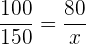
Mit KI zusammenfassen:













Ich habe den Kettensatz mit seinerzeit in der Handelsakademie gelernt . Er wurde vertikal angeordnet, was sehr übersichtlich war und man konnte es kaum verfehlen, die „richtigen“ Glieder zu verknüpfen. Ich erinnere mich nicht mehr genau daran, aber oft waren es auch 20 „Glieder“ in der vertikalen Anordnung. Ich fand diese Anschreibung viel einfacher.