
Wiederholung: Arten von Proportionalität
In Teil I hast du bereits gelernt, dass Zuordnungen proportional oder umgekehrt proportional sein können.
In den zehn folgenden Aufgaben hast du die Möglichkeit, dein Wissen praktisch anzuwenden.
Gemischte Aufgaben
Ein Großvater verteilt 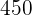 auf seine drei Enkel, die
auf seine drei Enkel, die  und
und  Jahre alt sind, proportional zu ihrem jeweiligen Alter. Wie viel Geld erhält jeder Enkel?
Jahre alt sind, proportional zu ihrem jeweiligen Alter. Wie viel Geld erhält jeder Enkel?
Ein Großvater verteilt 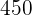 auf seine drei Enkel, die
auf seine drei Enkel, die  und
und  Jahre alt sind, proportional zu ihrem jeweiligen Alter. Wie viel Geld erhält jeder Enkel?
Jahre alt sind, proportional zu ihrem jeweiligen Alter. Wie viel Geld erhält jeder Enkel?
1 Es handelt sich um eine proportionale Zuordnung, daher können folgende Gleichungen aufgestellt werden:

2 Löse nach jeder Unbekannten auf:
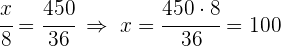
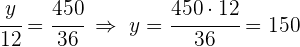
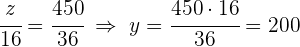
Drei Geschäftspartner schließen sich zusammen und steuern je 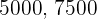 und
und 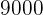 Euro zu einem Projekt bei. Nach einem Jahr haben sie
Euro zu einem Projekt bei. Nach einem Jahr haben sie 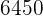 Gewinn gemacht.
Gewinn gemacht.
Wie viel Geld steht jedem einzelnen zu, damit die Auszahlung an jeden proportional zum anfänglichen Beitrag ist?
Drei Geschäftspartner schließen sich zusammen und steuern je 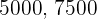 und
und 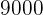 Euro zu einem Projekt bei. Nach einem Jahr haben sie
Euro zu einem Projekt bei. Nach einem Jahr haben sie 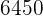 Gewinn gemacht.Wie viel Geld steht jedem einzelnen zu, damit die Auszahlung an jeden proportional zum anfänglichen Beitrag ist?
Gewinn gemacht.Wie viel Geld steht jedem einzelnen zu, damit die Auszahlung an jeden proportional zum anfänglichen Beitrag ist?
1 Es handelt sich um eine proportionale Zuordnung, daher können folgende Gleichungen aufgestellt werden:
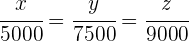
 2 Löse nach jeder Unbekannten auf
2 Löse nach jeder Unbekannten auf
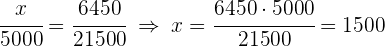
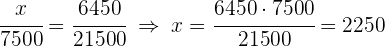
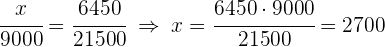
Drei zu 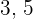 und
und  proportionale Geldbeträge werden unter drei Personen aufgeteilt. Wenn die zweite Person
proportionale Geldbeträge werden unter drei Personen aufgeteilt. Wenn die zweite Person 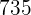 erhält, welchen Betrag erhalten dann die erste und dritte Person entsprechend?
erhält, welchen Betrag erhalten dann die erste und dritte Person entsprechend?
Drei zu 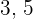 und
und  proportionale Geldbeträge werden unter drei Personen aufgeteilt. Wenn die zweite Person
proportionale Geldbeträge werden unter drei Personen aufgeteilt. Wenn die zweite Person 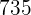 erhält, welchen Betrag erhalten dann die erste und dritte Person entsprechend?
erhält, welchen Betrag erhalten dann die erste und dritte Person entsprechend?
1 Es handelt sich um eine proportionale Zuordnung, daher können folgende Gleichungen aufgestellt werden:
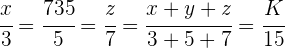
2 Ermittle die fehlenden Unbekannten:
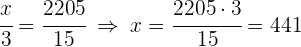

Drei zu  und
und  entsprechend proportionale Geldbeträge werden unter drei Personen aufgeteilt. Die jüngste Person erhält
entsprechend proportionale Geldbeträge werden unter drei Personen aufgeteilt. Die jüngste Person erhält 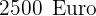 Wie viel Geld erhalten die beiden älteren Personen entsprechend?
Wie viel Geld erhalten die beiden älteren Personen entsprechend?
Drei zu  und
und  entsprechend proportionale Geldbeträge werden unter drei Personen aufgeteilt. Die jüngste Person erhält
entsprechend proportionale Geldbeträge werden unter drei Personen aufgeteilt. Die jüngste Person erhält 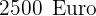 Wie viel Geld erhalten die beiden älteren Personen entsprechend?
Wie viel Geld erhalten die beiden älteren Personen entsprechend?
1 Stelle die Gleichungen der proportionalen Zuordnung auf und ermittle die fehlenden Unbekannten:
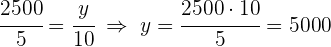

Drei Geschwister zahlen jährlich einen Betrag von 5900 € auf ein Familienkonto ein. Wenn sie 20, 24 und 32 Jahre alt sind und die Beiträge umgekehrt proportional zu ihrem Alter, wie viel trägt dann jeder jährlich bei?
Drei Geschwister zahlen jährlich einen Betrag von 5900 € auf ein Familienkonto ein. Wenn sie 20, 24 und 32 Jahre alt sind und die Beiträge umgekehrt proportional zu ihrem Alter, wie viel trägt dann jeder jährlich bei?
1 Da es sich um eine umgekehrt proportionale Zuordnung handelt, müssen die Kehrwerte der Altersangaben zur Berechnung herangezogen werden:

2 Suche den gemeinsamen Nenner
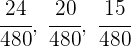
3 Führe eine Zuordnung durch, die proportional zu den Werten der Zähler  und
und  ist:
ist:

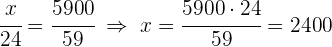
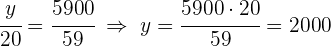
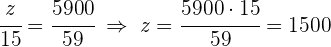
Teile 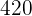 unter drei Kindern umgekehrt proportional zu ihrem jeweiligen Alter von
unter drei Kindern umgekehrt proportional zu ihrem jeweiligen Alter von 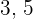 und
und  Jahren auf.
Jahren auf.
Teile 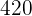 unter drei Kindern umgekehrt proportional zu ihrem jeweiligen Alter von
unter drei Kindern umgekehrt proportional zu ihrem jeweiligen Alter von 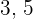 und
und  Jahren auf.
Jahren auf.
Lösungen:
1 Da es sich um eine umgekehrt proportionale Zuordnung handelt, müssen die Kehrwerte der Altersangaben zur Berechnung herangezogen werden:

2 Suche den gemeinsamen Nenner
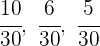
3 Führe eine Zuordnung durch, die proportional zu den Werten der Zähler 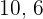 und
und  ist:
ist:
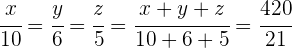
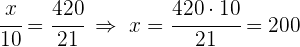

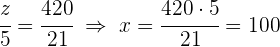
Über welchen Zeitraum muss ein Kapital von 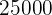 mit
mit 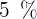 Zinsen angelegt werden, damit man
Zinsen angelegt werden, damit man 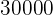 erhält?
erhält?
Über welchen Zeitraum muss ein Kapital von 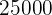 mit
mit 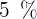 Zinsen angelegt werden, damit man
Zinsen angelegt werden, damit man 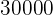 erhält?
erhält?
Lösungen:
1 Ermittle die Gesamtsumme der Zinsen:
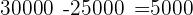
 Jahre
Jahre
Eine Person legt 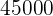 auf einem Konto an. Nach einem Jahr,
auf einem Konto an. Nach einem Jahr,  Monaten und
Monaten und  Tagen hat sich die Anlage auf
Tagen hat sich die Anlage auf 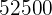 erhöht. Zu welchem Zinssatz wurde das Geld angelegt?
erhöht. Zu welchem Zinssatz wurde das Geld angelegt?
Eine Person legt 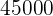 auf einem Konto an. Nach einem Jahr,
auf einem Konto an. Nach einem Jahr,  Monaten und
Monaten und  Tagen hat sich die Anlage auf
Tagen hat sich die Anlage auf 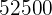 erhöht. Zu welchem Zinssatz wurde das Geld angelegt?Lösungen:
erhöht. Zu welchem Zinssatz wurde das Geld angelegt?Lösungen:
1 Rechne den Zeitraum in Tage um:
 Tage
Tage
2 Berechne die Zinsen:
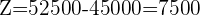
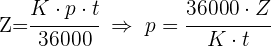
3 Ermittle den Umsatz (in %)

Zu welchem Zinssatz muss ein Kapital angelegt werden, damit man nach Ablauf von  Jahren eine Summe in Höhe des Startkapitals an Zinsen erhalten hat?
Jahren eine Summe in Höhe des Startkapitals an Zinsen erhalten hat?
Zu welchem Zinssatz muss ein Kapital angelegt werden, damit man nach Ablauf von  Jahren eine Summe in Höhe des Startkapitals an Zinsen erhalten hat?Lösungen:
Jahren eine Summe in Höhe des Startkapitals an Zinsen erhalten hat?Lösungen:
1 Die Höhe der Zinsen ist gleich dem Wert des Startkapitals
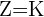
2 Ersetze  durch die Zinsformel:
durch die Zinsformel:
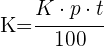
3 Das Produkt der Extremwerte ist gleich dem Produkt der Mittelwerte
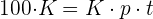
4 Mit  ist
ist  . Auf diese Weise kann der Gewinn ermittelt werden
. Auf diese Weise kann der Gewinn ermittelt werden
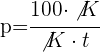
5 Vereinfache den Bruch
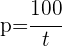
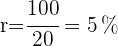
Über welchen Zeitraum muss ein Kapital zu 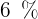 angelegt werden, um es zu verdreifachen?
angelegt werden, um es zu verdreifachen?
Über welchen Zeitraum muss ein Kapital zu 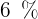 angelegt werden, um es zu verdreifachen?
angelegt werden, um es zu verdreifachen?
Lösungen:
1 Die Zinsen sind dreimal so hoch wie das Startkapital.
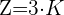
2 Wende die Zinsformel an, löse nach t auf und vereinfache:

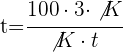
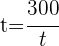
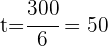 Jahre.
Jahre.
Mit KI zusammenfassen:













Ich habe den Kettensatz mit seinerzeit in der Handelsakademie gelernt . Er wurde vertikal angeordnet, was sehr übersichtlich war und man konnte es kaum verfehlen, die „richtigen“ Glieder zu verknüpfen. Ich erinnere mich nicht mehr genau daran, aber oft waren es auch 20 „Glieder“ in der vertikalen Anordnung. Ich fand diese Anschreibung viel einfacher.