1 Ein Großvater verteilt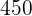 
an seine drei Enkel im Alter von 
und 
Jahren, proportional zu ihrem Alter. Wie viel erhält jedes Enkelkind?
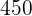an seine Enkel im Alter von
und
Jahren, proportional zu ihrem Alter. Wie viel erhält jedes Enkelkind?
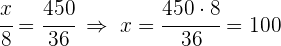
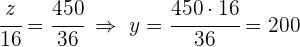
2 Drei Geschäftspartner investieren jeweils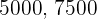
und
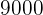. Nach einem Jahr haben Sie
verdient. Welcher Betrag steht jedem von ihnen zu, wenn sie eine zu ihrer Investition direkt proportionale Verteilung vornehmen?
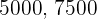und
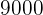. Nach einem Jahr haben Sie
verdient.Welcher Betrag steht jedem von ihnen zu, wenn sie eine zu ihrer Investition direkt proportionale Verteilung vornehmen?
1 Da es sich um ein Problem der direkten Proportionalität handelt, können wir folgende Gleichungen aufstellen
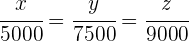
2 Wir lösen nach jeder Unbekannten auf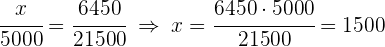
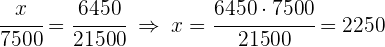
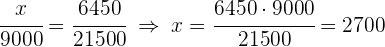
3 Eine bestimmter Betrag wird auf drei Personen verteilt, direkt proportional zu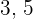
und
. Der zweiten Person stehen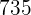
zu. Ermittle, wie viel den anderen beiden Personen zusteht.
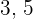und
. Der zweiten Person stehen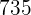
zu. Ermittle, wie viel den anderen beiden Personen zusteht.1 Da es sich um ein Problem der direkten Proportionalität handelt, können wir folgende Gleichungen aufstellen
2 Wir berechnen die fehlenden Unbekannten
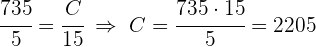
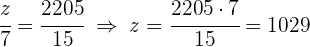
4 Geld wird proportional zu
und
verteilt; das jüngste Kind erhält
. Wie viel erhalten die beiden anderen Kinder?
und
verteilt; das jüngste Kind erhält
. Wie viel erhalten die beiden anderen Kinder?
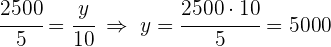
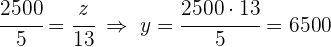
5 Drei Geschwister unterstützen die Familie jährlich mit 5900 €. Sie sind 20, 24 und 32 Jahre alt und ihre jährlichen Beiträge sind umgekehrt proportional zu ihrem Alter. Wie viel trägt jeder bei?
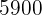. Sie sind
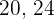und
Jahre alt und ihre jährlichen Beiträge sind umgekehrt proportional zu ihrem Alter. Wie viel trägt jeder bei? Lösungen
1 Da es sich um eine umgekehrt proportionale Verteilung handelt, müssen wir jeweils das umgekehrte Alter nehmen
2 Wir bringen die Brüche auf einen gemeinsamen Nenner
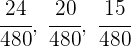
3 Wir führen eine zu den Zählern direkt proportionale Verteilung durch: 
und 
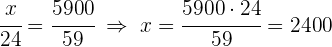
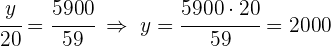
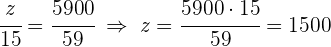
6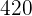
werden auf drei Kinder umgekehrt proportional zu ihrem Alter von
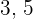und
Jahren verteilt.
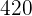werden auf drei Kinder umgekehrt proportional zu ihrem Alter von
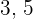und
Jahren verteilt.
1 Da es sich um eine umgekehrt proportinale Verteilung handelt, müssen wir das umgekehrte Alter nehmen
2 Wir bringen die Brüche auf einen gemeinsamen Nenner
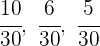
3 Wir führen eine zu den Zählern direkt proportionale Verteilung durch: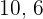 
und 
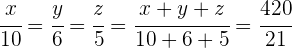
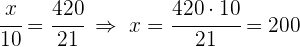
7 Wie lange muss man Kapital im Wert von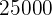
zu
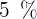Zinsen anlegen, damit man am Ende
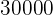erhält?
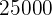zu
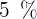Zinsen anlegen, damit man am Ende
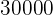erhält?
1 Wir berechnen die erhaltenen Zinsen:
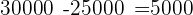
Jahre
8 Es werden
verliehen und nach einem Jahr,
Monaten und
Tagen erhält man
. Berechne den Prozentsatz der Zinsen.
verliehen und nach einem Jahr,
Monaten und
Tagen erhält man
. Berechne den Prozentsatz der Zinsen. Lösungen:
1 Wir berechnen die Zeit in Tagen
Tage
2 Wir berechnen die Zinsen
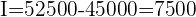
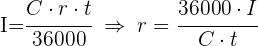
3 Wir berechnen die Rendite
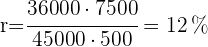
9Berechne den Prozentsatz des einfachen Zinses, zu dem ein bestimmtes Kapital verliehen werden muss, damit nach
Jahren die Zinsen dem verliehenen Kapital entsprechen.
Jahren die Zinsen dem verliehenen Kapital entsprechen. Lösungen:
1 Die Zinsen sind gleich dem Kapital
2 Wir setzen 
in die Zinsformel ein
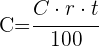
3 Die Produkte aus den Außengliedern sind gleich dem Produkt aus den Innengliedern
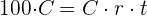
4 Wenn 
, gilt 
. Auf diese Weise können wir die Rendite ermitteln
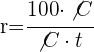
5 Wir vereinfachen den Bruch
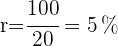
10Wie lange dauert es, bis sich ein Kapital, das zu einem Zinsatz von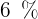
angelegt wurde, verdreifacht?
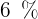angelegt wurde, verdreifacht?
1Die Zinsen sind gleich dem dreifachen Kapital
2Wir setzen in die entsprechende Formel ein und ermitteln so die Zeit und vereinfachen
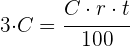
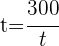
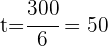Jahre.
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
Ich habe den Kettensatz mit seinerzeit in der Handelsakademie gelernt . Er wurde vertikal angeordnet, was sehr übersichtlich war und man konnte es kaum verfehlen, die „richtigen“ Glieder zu verknüpfen. Ich erinnere mich nicht mehr genau daran, aber oft waren es auch 20 „Glieder“ in der vertikalen Anordnung. Ich fand diese Anschreibung viel einfacher.