Kapitel
Definition: umgekehrt proportionale Größen
Zwei Werte sind zueinander umgekehrt proportional, wenn sich beim Erhöhen des einen der andere in der gleichen Proportion verringert. Wenn also
- einer der Werte mit einer beliebigen Zahl multipliziert wird, wird der andere durch dieselbe Zahl geteilt. Oder andersrum,
- wenn einer der Werte durch eine beliebige Zahl geteilt wird, wird die andere mit derselben Zahl multipliziert.
Wenn zwei Größen dem folgenden Schema entsprechen, bezeichnet man sie als umgekehrt proportional:
Je mehr, desto weniger.
Je weniger, desto mehr.
Und das immer in einem proportionalen Verhältnis, das bedeutet im Detail:
Das Doppelte des einen Werts entspricht der Hälfte des anderen.
Das Dreifache des einen Werts entspricht einem Drittel des anderen.
Beispiele: umgekehrt proportionale Größen
1 Mann nehme an, dass 3 Maler 20 Tage benötigen, um eine Wand zu streichen.
Logischerweise würde sich die Arbeitszeit um die Hälfte verringern, wenn die doppelte Anzahl von Malern daran arbeiten würde, das heißt 6 Maler würden 10 Tage benötigen.
Umgekehrt würden die Maler dreimal mehr Zeit benötigen, wenn nur ein Drittel von ihnen arbeiten würde. 1 Maler würde also 60 Tage benötigen. Da wir nun wissen, wie lange 1 Maler benötigen würde, können wir die folgende Tabelle aufstellen:
Die Zahl der Maler ist also umgekehrt proportional zur Zeit, die sie benötigen.
Je höher die Zahl der Personen, desto weniger Zeit.
Je niedriger die Zahl der Personen, desto mehr Zeit.
2 Man nehme an, dass ein Fahrzeug bei einer Geschwindigkeit von 60 km/h 6 Stunden benötigt, um eine bestimmte Strecke zurückzulegen.
Die Geschwindigkeit und die Zeit sind wieder umgekehrt proportional zueinander:
Je höher die Geschwindigkeit, desto weniger Zeit.
Je niedriger die Geschwindigkeit, desto mehr Zeit.
Wenn wir die Geschwindigkeit also verdoppeln, halbiert sich die benötigte Zeit. Das heißt, wenn die Geschwindigkeit 120 km/h beträgt, benötigt man nur noch 3 Stunden für die Wegstrecke.
Das heißt, wenn eine Größe zunimmt, nimmt die andere ab.
Aufgaben: umgekehrt proportionale Größen mit dem einfachen Dreisatz berechnen
1 Mit einem Wasserhahn, aus dem 
l Wasser pro Minute fließen, kann ein Wasserkanister innerhalb von 
Stunden gefüllt werden. Wie lange würde man benötigen, wenn 
l pro Minute aus dem Hahn fließen würden?
Es handelt sich um umgekehrt proportionale Größen, da man mehr Zeit für das Befüllen des Kanisters benötigt, je weniger Liter pro Minute aus dem Hahn fließen .
Lösung:
l/min 
h
l/min 
h
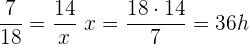
2 3 Arbeiter benötigen für den Bau einer Mauer 
Stunden. Wie lange würden 
Arbeiter dafür benötigen?
Es handelt sich um umgekehrt proportionale Größen, da man weniger Zeit benötigt, je mehr Arbeiter es sind.
Lösung:
Arbeiter 
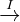
h
Arbeiter h
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
