Der Satz des Pythagoras gehört zu den bekanntesten mathematischen Theoremen und bildet eine fundamentale Grundlage der Geometrie. Benannt nach einem großen Mathematiker und Wissenschaftler besagt er, dass in einem rechtwinkligen Dreieck die Summe der Quadrate der beiden Kathetenlängen gleich dem Quadrat der Hypotenusenlänge.
Doch wer war eigentlich Pythagoras, der Namensgeber dieses Satzes? War er wirklich sein Erfinder, oder geht das Wissen darüber auf noch ältere Kulturen zurück? In diesem Artikel werfen wir einen Blick auf den berühmten Satz, seine historischen Ursprünge und seine Bedeutung für die Mathematik.
Satz des Pythagoras
Der Satz des Pythagoras ist einer der bekanntesten mathematischen Theoreme und spielt eine zentrale Rolle in der Geometrie.
Er beschreibt die Beziehung zwischen den Seitenlängen eines rechtwinkligen Dreiecks und lautet:
a² + b² = c²
Dabei sind a und b die Katheten (die kürzeren Seiten des Dreiecks), während c die Hypotenuse ist, also die längste Seite gegenüber dem rechten Winkel. Dieser Satz ermöglicht es, unbekannte Seitenlängen zu berechnen und wird in vielen Bereichen der Mathematik angewendet.
Und wer hat den Satz des Pythagoras erfunden?
Wenn Du den Beweis für den Satz verstehen möchtest, dann hilft dir Nachhilfe Mathe.
Historische Ursprünge des Satzes
Wahrscheinlich ist dieser Satz gar nicht von Pythagoras selbst entdeckt worden. Gravierte Tontafeln der Babyloniern (aber auch de Inder) zeigen, dass das Wissen über die Länge der Dreiecke bereits vor Pythagoras bekannt war, nämlich bereits:
v. Chr.
Sie kannten bereits spezielle Zahlenverhältnisse – sogenannte pythagoreische Tripel – die dem Satz entsprechen. In China wurde eine ähnliche Regel im alten Mathematikwerk Zhoubi Suanjing erwähnt.
Pythagoras übersetzte dieses Wissen jedoch in eine genau definierte Theorie. Seine Schule versuchte, einen Beweis für das Theorem zu finden.
Die Pythagoras Formel
Der griechische Mathematiker Pythagoras von Samos lieferte folgende Definition, auch bekannt als Pythagoras Formel:
Wenn die drei Seiten eines rechtwinkligen Dreiecks A, B und C heißen, mit dem Buchstaben C für die Hypotenuse, dann ist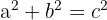 
. Die Summe der Flächeninhalte der Kathetenquadrate ist also gleich dem Flächeninhalt des Hypotenusenquadrates.
Der Satz begegnet dir auch, wenn es um die euklidische Geometrie geht.
Die Umkehrung des Satzes gilt ebenso: Gilt die Gleichung 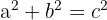in einem Dreieck mit den Seitenlängen a, b und c, so ist dieses Dreieck rechtwinklig, wobei der rechte Winkel der Seite c gegenüberliegt.
Diese Formel ermöglicht es dann, die Länge einer Seite eines rechtwinkligen Dreiecks zu berechnen oder zu beweisen, dass ein Dreieck rechtwinkelig ist. Wenn das Quadrat der längsten Seite gleich der Summe der Quadrate der beiden anderen Seiten ist, dann ist dieses Dreieck ein rechtwinkliges Dreieck.
Anwendungen des Satzes von Pythagoras
Das Theorem findet in vielen Bereichen Anwendung.
Geometrie
Seitenlängen
Diagonalen
Physik / Technik
Bauplanung
Navigation
Optik
Navigation
Bestimmung kurzer Distanz
Luft- oder Schifffahrtsrouten
Kein Wunder also, dass der Beweis so wichtig ist!
Wer war Pythagoras?
Pythagoras wuchs zu einem der größten Mathematiker der Geschichte heran. Er gilt als eine der bedeutendsten Figuren der Antike, obwohl viele seiner Lehren und Entdeckungen nicht direkt von ihm selbst überliefert, sondern erst durch spätere Anhänger weitergegeben wurden.
Auch der Mathematiker Archimedes prägte die Wissenschaft mit seinen Erkenntnissen.
Leben und Wirken
Pythagoras wurde auf der griechischen Insel Samos geboren und reiste in jungen Jahren vermutlich zu Studienzwecken nach Ägypten und Babylon, wo er sich mathematisches und astronomisches Wissen aneignete. Er interessierte sich für Philosophie, Geschichte und Wissenschaft.
Zurück auf der Insel Samos, lehrte Pythagoras zunächst in einem Amphitheater, jedoch ohne großen Erfolg. Der aus der Stadt verbannte Wissenschaftler reiste ins damalige Kroton (im heutigen Süditalien) und gründete dort eine Schule – eine Art philosophisch-mathematische Bruderschaft.
Sein ganzes Leben lang sucht er die Mathematik mit der Philosophie zu vereinen. Viele Schüler folgten ihm und unterstützten ihn bei seinen Experimenten und Forschungen.
Pythagoras starb ungefähr 500 v. Chr., aber auch hier sind die Umstände seines Todes nicht genau bekannt. Sein Einfluss in Mathematik, Naturwissenschaften und Philosophie blieb über Jahrhunderte hinweg bestehen.
Legenden und Einfluss
Da Pythagoras selbst keine schriftlichen Aufzeichnungen hinterließ, sind viele seiner Lehren und sein Leben von Mythen umrankt. Eine davon dreht sich um seine jungen Jahre!
Auch um die Erfindungen von Isaac Newton ranken sich einige Legenden.
Einige Monate vor seiner Geburt hätte ein Orakel dem Vater von Pythagoras die Geburt eines begabten Kindes vorausgesagt. Pythagoras bedeutet also "angekündigt von Pythia". Und genau wie das Orakel vorausgesagt hatte, erweist sich Pythagoras als ein sehr talentiertes Kind und gewann der Legende nach im Alter von 18 Jahren in allen Disziplinen der Olympischen Spiele.
So wurde ihm eine fast göttliche Weisheit nachgesagt und seine Anhänger betrachteten ihn als eine übermenschliche Figur.
Pythagoras und die Mathematik
Pythagoras war ein Alleskönner. Seiner Meinung nach sollte die Mathematik auch für andere Fächer wie Musik oder Philosophie genutzt werden. Seines ganzes Leben lang forscht er und beweist mit Hilfe seiner Schüler neue mathematische Entdeckungen.
Im Zusammenhang mit der Musik erkannte er:
- Den Zusammenhang zwischen der Länge einer vibrierenden Saite und der Tonhöhe der auf dieser Saite gespielten Note.
- Er experimentierte auch mit Gläsern mit unterschiedlichem Wasserstand, wobei jeder Wasserstand eine Musiknote repräsentiert.
Wie wäre es mit Mathe Nachhilfe online?
Er entdeckte, dass die Summe aller Winkel eines Dreiecks immer 180 ° entspricht und spielt mit der Berechnung von Durchschnitten und Anteilen. Schauen wir uns einige Errungenschaften an!
Die Wurzelschnecke von Pythagoras
Die pythagoreische Schnecke ist ein Werkzeug zur geometrischen Visualisierung der Quadratwurzeln aufeinanderfolgender ganzer Zahlen. Sie basiert auf dem Satz des Pythagoras und zeigt, wie sich Wurzeln aus ganzen Zahlen schrittweise konstruieren lassen.
So konstruiert man die Wurzelschnecke:
- Zunächst zeichnest Du ein rechtwinkliges Dreieck, dessen Seiten des rechten Winkels den Wert 1 haben (Hypotenuse dieses Dreiecks hat die Länge √2)
- An die Hypotenuse des ersten Dreiecks wird ein neues rechtwinkliges Dreieck angefügt, das wieder eine Kathetenlänge von 1 hat (Hypotenuse dieses Dreiecks hat die Länge √3)
- Dieser Prozess wird fortgesetzt, wobei jedes neue Dreieck auf der vorherigen Hypotenuse aufbaut und immer eine Kathete der Länge 1 hat.
- So entstehen sukzessive Dreiecke mit Hypotenusen der Länge √2, √3, √4, √5, ... wodurch eine spiralförmige Struktur entsteht.
Wenn man sich mit Mathe beschäftigt, dann kommt man immer auch auf René Descartes zu sprechen.
Dank dieses Werkzeugs kennst Du dann die Quadratwurzeln der aufeinanderfolgenden ganzen Zahlen, die den Längen der Hypotenusen der rechtwinkligen Dreiecke entsprechen.
Die Tafel von Pythagoras
Diese Tabelle wird häufig verwendet, um Kindern (und Erwachsenen) das Einmaleins beizubringen. Die Tafel von Pythagoras ist einfach:
Die Werte der Spalte multiplizieren sich mit den Werten der Zeile. Die Antwort wird am Schnittpunkt der beiden Werte in der Tabelle angegeben.
Die Tafel ist intuitiv verständlich und vor allem auf visuelles Lernen ausgelegt!
Die Schule der Pythagoreer
Pythagoras wollte Mathematik lehren und Gleichgesinnte finden, die ihn bei seinen wissenschaftlichen Forschungen halfen. Deshalb gründete er in Cortona, im Süden Italiens, eine Schule. Die Mitglieder der Schule diskutierten über Wissenschaft, aber auch über:
Philosophie
Politik
Religion
Für Pythagoras hängt all das mit der Mathematik zusammen. Alle Bereiche - die Natur, der Staat, die Familie - all das unterliege denselben zahlenmäßig ausdrückbaren Gesetzmäßigkeiten. Die Zahl steht für die Schüler Pythagoras' im Zentrum von allem.
Die Zahl ist das Wesen aller Dinge
Pythagoras
Die Schule bestand über 150 Jahre und zählte insgesamt 218 Mitglieder, die Pythagoreer. Die Forschungen der Pythagoreer wurden zusammengefasst, sodass man im Nachhinein die Identität der Erfinder der einzelnen Formeln kaum kennt.
Kennst Du schon den Strahlensatz von Thales?
Auch um die Pythagoreer rankten sich, ähnlich wie um Pythagoras selbst, zahlreiche Mythen. Sie hatten sogar ein geheimnisvolles Symbol: Die Pythagoräer hatten einen Weg gefunden, ein regelmäßiges Fünfeck zu zeichnen, eine Figur, deren fünf Seiten gleich sind.
Dazu verwendeten sie fünf gleichseitige Dreiecke, die ein Pentagramm bildeten. Pythagoras verwandte das Pentagramm als Symbol für Gesundheit. Seine Anhänger trugen es als Erkennungszeichen, deshalb wird es heute noch das Zeichen der Pythagoreer genannt.
Dir gefällt unser Artikel? Hinterlasse eine Bewertung!
Loading...
