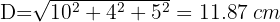Berechne in Kubikzentimetern das Volumen eines Hauses, das 
m lang, 
m breit und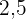 
m hoch ist.
Berechne in Kubikzentimetern das Volumen eines Hauses, das m lang, m breit und 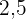m hoch ist.
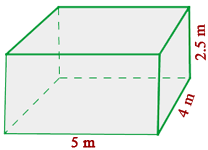
Wir berechnen das Volumen
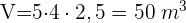
Wir wissen, dass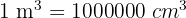 
und rechnen um:
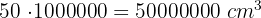
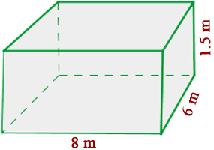
Ein Swimmingpool ist 
lang, 
m breit und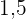 
m tief. Der Pool soll gestrichen werden, was € pro Quadratmeter kosten soll.
- Wie hoch sind die Gesamtkosten?
- Wie viele Liter Wasser werden benötigt, um den Pool zu befüllen?
1 Wir berechnen die Fläche, die gestrichen werden soll
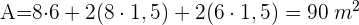
2 Wir berechnen die Kosten
€
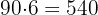3 Die zum Füllen des Pools benötigten Liter ergeben sich aus dem Volumen des Pools multipliziert mit 1000.
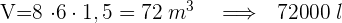
In einem Lager mit einer Länge von 5 m, einer Breite von 3 m und einer Höhe von 2 m sollen Kartons mit einer Länge von 10 dm, einer Breite von 6 dm und einer Höhe von 4 dm eingelagert werden. Wie viele Kartons können untergebracht werden?
In einem Lager mit einer Länge von 5 m, einer Breite von 3 m und einer Höhe von 2 m sollen Kartons mit einer Länge von 10 dm, einer Breite von 6 dm und einer Höhe von 4 dm eingelagert werden. Wie viele Kartons können untergebracht werden?
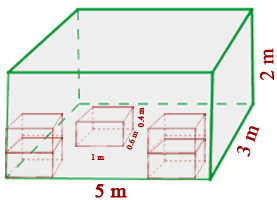
1 Wir stellen fest, dass
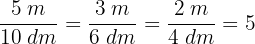
2 Wir berechnen das Volumen des Lagers
3 Wir berechnen das Volumen der Kisten
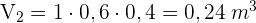
4 Die Anzahl der Kisten ergibt sich aus dem Volumen des Lagers dividiert durch das Volumen einer Kiste.
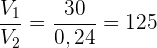Kisten
Ermittle die Gesamtfläche eines Tetraeders, eines Oktaeders und eines Ikosaeders mit einer Kantenlänge von 5 cm.
Ermittle die Gesamtfläche eines Tetraeders, eines Oktaeders und eines Ikosaeders mit einer Kantenlänge von 5 cm.
1 Die Gesamtfläche eines Tetraeders ist
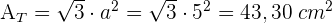
2 Die Gesamtfläche eines Oktaeders ist
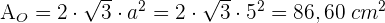
3 Die Gesamtfläche eines Ikosaeders ist
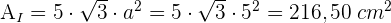
Berechne die Höhe eines Prismas mit einer Grundfläche von 
dm2 und einem Volumen von 
l.
1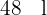 
entsprechen einem Volumen von 
2 Wir berechnen das Volumen des Prismas
3 Wir setzen die Volumen gleich
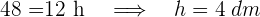
Berechne die Menge an Blech, die benötigt wird, um 
Dosen in Form eines Zylinders mit einem Durchmesser von cm und einer Höhe von 
cm herzustellen.
Berechne die Menge an Blech, die benötigt wird, um Dosen in Form eines Zylinders mit einem Durchmesser von cm und einer Höhe von cm herzustellen.
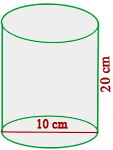
1 Wir berechnen die Gesamtfläche der Dose
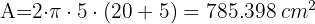
2 Für 10 Dosen wird folgende Menge benötigt
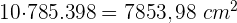
Die Höhe eines Zylinders ist genauso lang wie der Umfang der Grundfläche. Die Höhe beträgt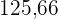 
cm. Berechne:
- Die Gesamtfläche.
- Das Volumen.
1 Wir berechnen den Radius
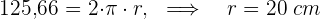
2 Wir berechnen die Gesamtfläche
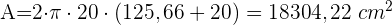
3 Wir berechnen das Volumen
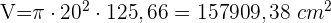
In einen Messzylinder mit einem Radius von cm werden vier Eiswürfel mit einer Kantenlänge von cm gegeben. Wie hoch steigt das Wasser, wenn die Eiswürfel schmelzen?
1 Wir berechnen das Volumen der Eiswürfel
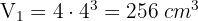
2 Da der Messzylinder zylindrisch ist, ist sein Volumen
3 Wir setzen die Volumen gleich und erhalten
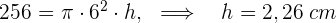
Wir setzen die Volumen gleich und erhalten
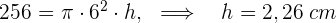
Die Kuppel einer Kathedrale ist eine Halbkugel mit einem Radius von 
m. Die Kuppel soll restauriert werden und es werden 
€ pro m2 veranschlagt. Wie viel kostet die Restaurierung der Kuppel?
1 Wir berechnen die Fläche der Halbkuppel
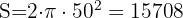
2 Die Restaurierung kostet
€
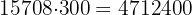Wie viele quadratische Fliesen mit einer Seitenlänge von cm werden benötigt, um die Seiten eines m langen, m breiten und 
m tiefen Swimmingpools zu bedecken?
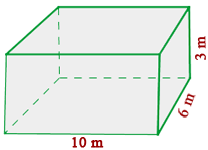
1 Wir berechnen die zu bedeckende Fläche
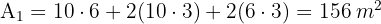
2 Wir berechnen die Fläche einer Fliese
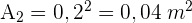
3 Die Anzahl der benötigten Fliesen ist
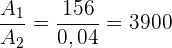
Ein zylindrisches Gefäß, das mit Wasser befüllt wird, hat einen Radius von cm und eine Höhe von cm. Wenn das Gefäß befüllt 
kg wiegt, was wiegt es ohne Inhalt?
1 Wir berechnen das Volumen
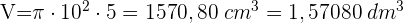
2 Das Gefäß wiegt
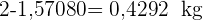
Luis macht für eine Party kegelförmige Hüte aus Pappe. Wie viel Pappe benötigt er, wenn die Hüte einen Radius von 
cm und eine Mantellinie von 
cm haben sollen?
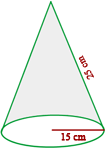
1 Wir berechnen die Fläche des Kegels
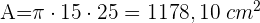
2 Für 10 Hüte wird folgende Fläche benötigt
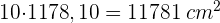
Ein Würfel mit einer Kantenlänge von cm ist mit Wasser gefüllt. Würde diese Wassermenge in eine Kugel mit einem Radius von passen?
1 Wir berechnen das Volumen des Würfels
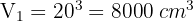
2 Wir berechnen das Volumen der Kugel
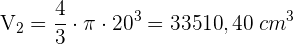
Da das Volumen der Kugel größer ist als das Volumen des Würfels, würde die Wassermenge hineinpassen.
Berechne die Diagonale eines Quaders mit einer Länge von 10 cm, einer Breite von cm und einer Höhe von cm.
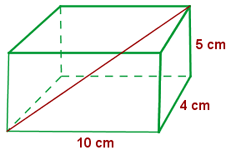
Die Diagonale ist gegeben durch
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
