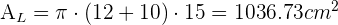Kapitel
Ein Kegelstumpf ist der geometrische Körper, der sich ergibt, wenn man einen Kegel durch eine Ebene parallel zur Kreisfläche schneidet und den Teil abtrennt, der die Spitze enthält.
Merkmale eines Kegelstumpfes
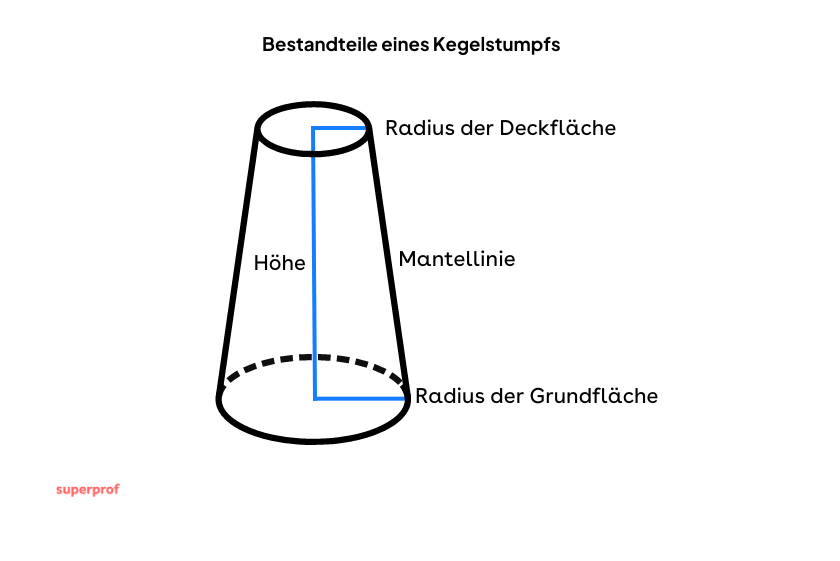
Der durch den Schnitt bestimmte Teil ist die Deckfläche.
Die Höhe ist das Segment, das die Grundfläche und die Deckfläche rechtwinklig verbindet
Die Radien sind die Radien der beiden kreisförmigen Flächen.
Die Mantellinie ist das Segment, das zwei Punkte auf dem Rand der beiden Flächen verbindet.
Formeln für Kegelstümpfe
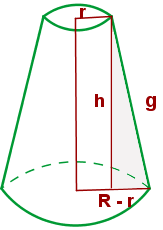
Die Mantellinie des Kegelstumpfes
Du erhältst die Mantellinie des Kegelstumpfes durch den Satz des Pythagoras auf das schraffierte Dreieck:
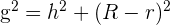
Seitenfläche eines Kegelstumpfes
Flächeninhalt eines Kegelstumpfes
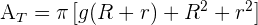
Volumen eines Kegelstumpfes
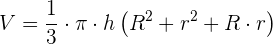
Beispiele für die Berechnung von Kegelstümpfen
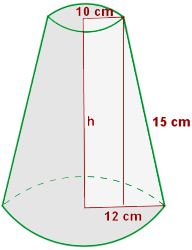
1 Berechne die Seitenfläche, die Gesamtfläche und das Volumen eines Kegelstumpfes mit den Radien 
und 
und der Höhe 
.
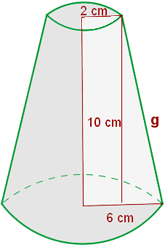
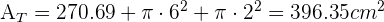
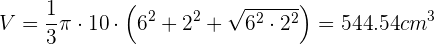
2 Berechne die Seitenfläche, die Gesamtfläche und das Volumen des Kegelstumpfs mit den Radien 
und 
cm und der Mantellinie 
cm.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
