Kapitel

Vorbereitende Konzepte
1. Größe. Eine Größe ist eine Eigenschaft, die numerisch gemessen werden kann. Zum Beispiel Gewicht, Masse, Länge, Volumen, Zeit usw. All diese Größen sind physikalische Systeme.
2. Verhältnis. Das Verhältnis von zwei vergleichbaren Größen zueinander ist der Quotient von diesen, dargestellt als Bruch (oder als Dezimalzahl oder ganze Zahl). Somit wird ein Verhältnis von einer Größe  zu einer Größe
zu einer Größe  wie folgt ausgedrückt
wie folgt ausgedrückt

und als  zu
zu 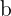 ausgesprochen.
ausgesprochen.
Der Zähler und der Nenner des Bruch sind die Glieder des Verhältnisses.
Beispiel:
Luis lernt täglich 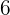 Stunden und spielt
Stunden und spielt  Stunden. Wie ist das Verhältnis zwischen den Stunden, die Luis täglich mit Lernen und Spielen verbringt?
Stunden. Wie ist das Verhältnis zwischen den Stunden, die Luis täglich mit Lernen und Spielen verbringt?
In diesem Fall ist das Vorderglied  , während das Hinterglied
, während das Hinterglied 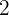 ist. Das Verhältnis ist also gegeben durch
ist. Das Verhältnis ist also gegeben durch

und somit 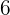 zu
zu 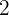 . Das Verhältnis sagt uns also, dass Luis für jede Stunde, die er mit Spielen verbringt, er drei Stunden mit Lernen verbringt (also
. Das Verhältnis sagt uns also, dass Luis für jede Stunde, die er mit Spielen verbringt, er drei Stunden mit Lernen verbringt (also 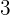 ).
).
Verhältnisgleichung
Eine Verhältnisgleichung ist eine Gleichung, die zwei Verhältnisse gleichsetzt. Wenn also zwei Verhältnisse  und
und  gegeben sind, haben wir eine Verhältnisgleichung, wenn
gegeben sind, haben wir eine Verhältnisgleichung, wenn

Die Verhältnisgleichung wird  verhält sich zu
verhält sich zu  wie
wie 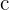 zu
zu  ausgesprochen. Außerdem werden
ausgesprochen. Außerdem werden  und
und  Außenglieder und
Außenglieder und  und
und 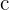 Innenglieder genannt.
Innenglieder genannt.
Für jede Verhältnisgleichung gilt, dass das Produkt aus den Außengliedern dem Produkt aus den Innengliedern entspricht. Wir erhalten 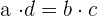 .
.
Beispiel. Wir sehen uns die Verhältnisse  und
und  an. Wir stellen fest, dass
an. Wir stellen fest, dass
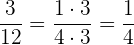
Wir haben eine Verhältnisgleichung, nämlich
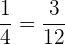 .
.
In diesem Beispiel haben wir die Außenglieder  und
und  und die Innenglieder
und die Innenglieder 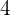 und
und 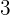 . Das Produkt aus den Außengliedern ist
. Das Produkt aus den Außengliedern ist

und das Produkt aus den Innengliedern ist
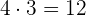 .
.
Beide Produkte liefern dasselbe Ergebnis.
Bei fortlaufenden Proportionen, zum Beispiel
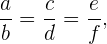
gilt, dass die Summe der Vorderglieder, dividiert durch die Summe der Hinterglieder der Verhältnisse der fortlaufenden Proportion gleich einem der Verhältnisse ist.
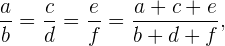
Wenn wir bei einer Verhältnisgleichung die Vorderglieder mit den Hintergliedern vertauschen, erhalten wir trotzdem eine Verhältnisgleichung. Zwei Verhältnisse sind also gleich
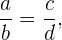
und somit auch ihre Kehrwerte
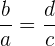 .
.
Beispiel:
Kehren wir zu dem Verhältnis des vorherigen Beispiels zurück
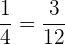 .
.
Wir nehmen den Kehrwert des ersten Verhältnisses und erhalten
 .
.
Wir nehmen den Kehrwert des zweiten Verhältnisses und erhalten
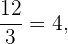
Daraus ergibt sich, dass die Kehrwerte der Verhältnisse ebenfalls gleich sind,
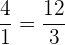 .
.
Vierte Proportionale
Eine vierte Proportionale ist irgendeiner der Terme einer Verhältnisgleichung. Zur Berechnung müssen wir zwei Fälle in Betracht ziehen:
- Wenn sie sich im Zähler des Verhältnisses befindet
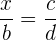 .
.
Wir berechnen also wie folgt
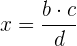 .
.
- Wenn sie sich im Nenner des Verhältnisses befindet
 .Wir berechnen wie folgt
.Wir berechnen wie folgt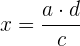 .
.
Wir stellen fest, dass wir einfach nur die vierte Proportionale streichen müssen.
Beispiel. Wir sehen uns folgende Verhältnisgleichung an
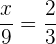 .
.
Wie groß ist die vierte Proportionale, gegeben durch den Term 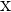 ? Wir berechnen
? Wir berechnen
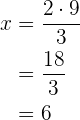
Mittlere Proportionale
Eine Verhältnisgleichung ist fortlaufend, wenn ihre Innenglieder gleich sind
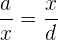 .
.
In diesem Fall nennt man die vierte Proportionale, die den Innengliedern entspricht, mittlere Proportionale. Außerdem können wir wie folgt berechnen
 .
.
Beispiel:
Wir sehen uns folgende Verhältnisgleichung an:
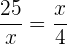 .
.
Wie groß ist die mittlere Proportionale, gegeben durch den Term 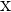 ? Wir berechnen
? Wir berechnen

Dritte Proportionale
Bei einer fortlaufenden Verhältnisgleichung nennt man jeden der ungleichen Terme dritte Proportionale.
Um die dritten Proportionalen zu berechnen, müssen wir zwei Fälle in Betracht ziehen:
- Wenn sie sich im Zähler des Verhältnisses befinden
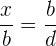 .
.
Es wird also wie folgt berechnet
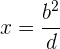 .
.
- Wenn sie sich im Nenner des Verhältnisses befinden
 .Es wird also wie folgt berechnet
.Es wird also wie folgt berechnet .
.
Wir beachten, dass in jedem Fall die dritte Proportionale dem Quadrat der mittleren Proportionale geteilt durch die andere dritte Proportionale entspricht.
Beispiel:
Wir sehen uns folgende Verhältnisgleichung an
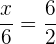 .
.
Wie groß ist die dritte Proportionale, gegeben durch den Term 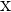 ? Wir berechnen
? Wir berechnen

Direkt proportionale Größen
Zwei Größen sind direkt proportional, wenn man eine von ihnen mit einer beliebigen Zahl multipliziert und die andere mit der gleichen Zahl multipliziert wird. Ebenso sind zwei Größen direkt proportional, wenn bei der Division der einen durch eine beliebige Zahl die andere durch die gleiche Zahl geteilt wird.
Es entsteht eine direkte Proportionalität zweier Größen, wenn:
- Je größer die erste Größe ist, desto größer ist die zweite Größe, und zwar im gleichen Verhältnis.
- Je kleiner die erste Größe, desto kleiner die zweite Größe, und zwar im gleichen Verhältnis.
Eine andere Möglichkeit, um festzustellen, ob zwei Größen direkt proportional sind, ist der Quotient aus ihnen. Der Quotient zwischen zwei direkt proportionalen Größen ist immer konstant.
Beispiel:
Das Gewicht eines Produkts und sein Preis sind zwei direkt proportionale Größen.
Wenn also  Tomaten
Tomaten  € kosten, gilt:
€ kosten, gilt:
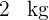 Tomaten kosten
Tomaten kosten 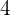 €
€ Tomaten kosten
Tomaten kosten  €
€
Der einfache Dreisatz
Bist du auf der Suche nach Nachhilfe in Mathe?
Der einfache Dreisatz besteht aus einem Verhältnis von Mengen mit direkter Proportionalität. Dieses tritt auf, wenn bei zwei Mengen, die direkt proportionalen Größen entsprechen, die Menge einer dieser Größen berechnet werden muss, die einer bestimmten Menge der anderen Größe entspricht.
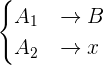

Beispiel. Ein Auto legt  in
in  Stunden zurück. Wie viele Kilometer hat das Auto nach
Stunden zurück. Wie viele Kilometer hat das Auto nach  Stunden zurückgelegt?
Stunden zurückgelegt?
Wir stellen fest, dass die Größen direkt proportional zueinander sind. Je weniger Stunden, desto weniger Kilometer werden zurückgelegt. Wir berechnen:
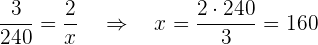
In  Stunden hat das Auto also
Stunden hat das Auto also  zurückgelegt.
zurückgelegt.
Direkt proportionale Verteilungen
Eine direkt proportionale Verteilung besteht darin, den Anteil zu berechnen, der jeder der gegebenen Größen entspricht. Gegeben sind hierbei Größen eines bestimmten Typs sowie eine Gesamtgröße. Wenn also 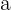 ,
,  und
und 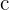 Größen vom gleichen Typ sind und wir eine Gesamtgröße von
Größen vom gleichen Typ sind und wir eine Gesamtgröße von  haben, möchten wir die Größen
haben, möchten wir die Größen 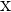 ,
, 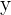 und
und 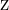 sowie
sowie  herausfinden und
herausfinden und

Beispiel. Ein Großvater verteilt 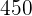 € auf seine drei Enkel im Alter von
€ auf seine drei Enkel im Alter von 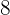 ,
,  und
und 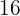 Jahren, proportional zu ihrem Alter. Wieviel erhält jeder?
Jahren, proportional zu ihrem Alter. Wieviel erhält jeder?
Zunächst nennen wir 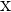 ,
, 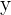 und
und 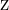 die Größen, die jedem der Enkelkinder entsprechen.
die Größen, die jedem der Enkelkinder entsprechen.
Die proportionale Verteilung lautet:

Jedes Enkelkind erhält:
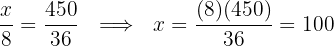

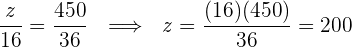
Prozentsätze
Ein Prozentsatz ist eine Art des Dreisatzes, bei der eine der Größen 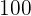 ist.
ist.
Beispiel. Ein Freund hat  € und soll davon
€ und soll davon 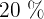 seinem Bruder geben. Wieviel Euro gibt er also seinem Bruder?
seinem Bruder geben. Wieviel Euro gibt er also seinem Bruder?
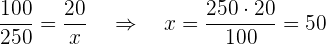
Er muss seinem Bruder also 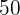 € geben.
€ geben.
Umgekehrt proportionale Größen
Zwei Größen sind dann umgekehrt proportional, wenn man eine Größe erhöht, die andere im gleichen Verhältnis kleiner wird. Dies geschieht, wenn:
- Multipliziert man eine von ihnen mit einer beliebigen Zahl, so wird die andere durch dieselbe Zahl geteilt.
- Dividiert man die eine Zahl durch eine beliebige Zahl, wird die andere mit der gleichen Zahl multipliziert.
Ein Verhältnis der umgekehrten Proportionalität besteht zwischen zwei Größen, wenn:
- Mehr ist gleichbedeutend mit weniger.
- Weniger ist gleichbedeutend mit mehr.
Beispiel:
Angenommen,  Maler benötigen
Maler benötigen 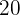 Tage für ein Wandgemälde. Wenn wir also die Anzahl der Maler verdoppeln, reduziert sich die Zeit um die Hälfte. Das heißt,
Tage für ein Wandgemälde. Wenn wir also die Anzahl der Maler verdoppeln, reduziert sich die Zeit um die Hälfte. Das heißt, 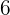 Maler benötigen
Maler benötigen 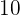 Tage.
Tage.
Verringert sich die Zahl der Maler auf ein Drittel, so ist die für dieselbe Aufgabe erforderliche Zeit dreimal so lang. Das heißt,  Maler benötigt
Maler benötigt  Tage. Wenn wir also wissen, wie lange ein Maler braucht, können wir folgende Tabelle erstellen:
Tage. Wenn wir also wissen, wie lange ein Maler braucht, können wir folgende Tabelle erstellen:

Die Anzahl der Personen, die eine Aufgabe ausführen, ist also umgekehrt proportional zu der Zeit, die sie benötigen.
Umgekehrter Dreisatz
Der umgekehrte Dreisatz besteht aus einem Verhältnis von Mengen mit umgekehrter Proportionalität, das auftritt, wenn bei zwei Mengen, die umgekehrt proportionalen Größen entsprechen, die Menge einer dieser Größen berechnet werden muss, die einer bestimmten Menge der anderen Größe entspricht.
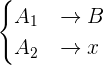
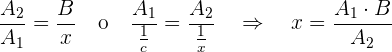
Beispiel:
Aus einem Wasserhahn laufen pro Minute 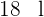 Wasser und es dauert
Wasser und es dauert 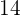 Stunden, bis ein Tank vollständig befüllt ist. Wie lange würde es dauern, wenn die Druchflussmenge
Stunden, bis ein Tank vollständig befüllt ist. Wie lange würde es dauern, wenn die Druchflussmenge  pro Minute beträgt?
pro Minute beträgt?
Wir beachten, dass es sich um umgekehrt proportionale Größen handelt. Je weniger Liter pro Minute, desto länger dauert es bis zur vollständigen Befüllung. Wir berechen also und haben folgendes Verhältnis
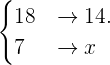
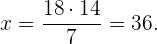
Wenn die Durchflussmenge also  pro Minute beträgt, dauert es
pro Minute beträgt, dauert es 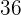 Stunden.
Stunden.
Umgekehrt proportionale Verteilungen
Eine umgekehrt proportionale Verteilung bedeutet, dass man bei einer Anzahl von Mengen gleicher Art und einer Gesamtmenge eine Verteilung vornehmen muss, die direkt proportional zu den Kehrwerten der Mengen ist. Wenn also 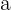 ,
,  und
und 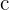 Größen vom gleichen Typ sind und wir eine Gesamtgröße von
Größen vom gleichen Typ sind und wir eine Gesamtgröße von  haben, möchten wir die Größen
haben, möchten wir die Größen 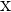 ,
, 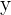 und
und 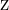 sowie
sowie  ermitteln und
ermitteln und
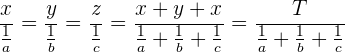
Beispiel:
Während der Verlesung eines Testaments verlas der Anwalt von Herrn Müller den folgenden Paragrafen bezüglich des Erbes, das seine Kinder erhalten sollten: "Meine Kinder: Hugo, Paco und Luis, ihr sollt gemeinsam 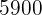 € erhalten. Die Verteilung sollte so erfolgen, dass ihr einen Betrag erhaltet, der umgekehrt proportional zu eurem Alter zum Zeitpunkt meines Todes ist.…” Hugo, Paco und Luis sind jeweils
€ erhalten. Die Verteilung sollte so erfolgen, dass ihr einen Betrag erhaltet, der umgekehrt proportional zu eurem Alter zum Zeitpunkt meines Todes ist.…” Hugo, Paco und Luis sind jeweils 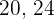 und
und  Jahre alt. Wie viel erhält jeder von ihnen?
Jahre alt. Wie viel erhält jeder von ihnen?
Da die Verteilung umgekehrt proportional ist, erhält das jüngere Kind einen größeren Anteil des Erbes, während das ältere Kind einen kleineren Anteil erhält. Dies lässt sich lösen, indem man die umgekehrten Altersstufen ermittelt und damit und mit dem Gesamtbetrag eine direkt proportionale Verteilung vornimmt.
1 Wir nehmen das umgekehrte Alter und bringen die Brüche auf einen gemeinsamen Nenner (denke daran, dass du das kgV anwenden kannst).
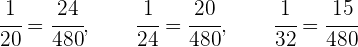
2 Wir nehmen eine direkt proportionale Verteilung dieser Brüche vor:
 und
und 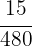 .
.
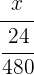 =
= 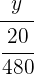 =
= 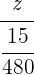 =
= 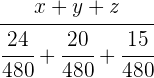 =
= 
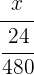 =
=  ⇒
⇒ 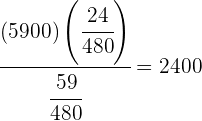 €
€
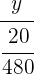 =
=  ⇒
⇒  €
€
 =
=  ⇒
⇒ 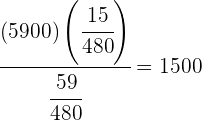 €
€
Hugo erhält also  €, Paco
€, Paco  € und Luis
€ und Luis  €.
€.
Zusammengesetzte Proportionalität
Die zusammengesetzte Proportionalität wird verwendet, wenn drei oder mehr Größen miteinander in Beziehung stehen. Zwischen den Größen lassen sich direkte und umgekehrte Proportionalitätsbeziehungen herstellen, sodass drei Fälle unterschieden werden können: direkte zusammengesetzte Proportionalität, zusammengesetzte Proportionalität, direkt-umgekehrt zusammengesetzte Proportionalität.
Zusammengesetzter Dreisatz
Der zusammengesetzte Dreisatz wird verwendet, wenn drei oder mehr Größen miteinander in Beziehung stehen,
sodass wir aus den Beziehungen zwischen den bekannten Größen die unbekannte Größe erhalten.
Da zwischen den Größen direkte oder umgekehrte Proportionalitätsbeziehungen hergestellt werden können, können wir drei Fälle des zusammengesetzten Dreisatzes unterscheiden.
Zins
Zinsen sind die Rendite für geliehenes Geld. Dieser Ertrag steht in direktem Verhältnis zur Höhe des geliehenen Betrags und der Laufzeit des Darlehens.
| Konzept | Name | Symbole |
|---|---|---|
| Geliehener Betrag | Kapital | C |
| Laufzeit des Darlehens | Laufzeit | t |
| Gewinn pro 100 € in einem Jahr | Rendite | r |
| Darlehensertrag | Zins | l |

Wenn die Zeit in Monaten ausgedrückt wird:
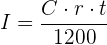
Mit KI zusammenfassen:













Ich habe den Kettensatz mit seinerzeit in der Handelsakademie gelernt . Er wurde vertikal angeordnet, was sehr übersichtlich war und man konnte es kaum verfehlen, die „richtigen“ Glieder zu verknüpfen. Ich erinnere mich nicht mehr genau daran, aber oft waren es auch 20 „Glieder“ in der vertikalen Anordnung. Ich fand diese Anschreibung viel einfacher.