Kapitel
Volumen und Fläche des Prismas
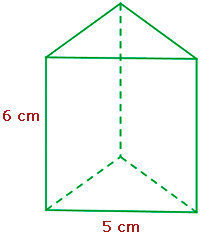
Bestimme die Gesamtfläche und das Volumen eines dreieckigen Prismas mit der Höhe 6 cm und der Grundfläche eines gleichseitigen Dreiecks mit der Seitenlänge 5 cm. Runde auf zwei Dezimalstellen.
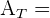
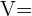
Dieses Feld ist erforderlich.
1 Zunächst berechnen wir den Umfang der Grundfläche, der bei einem gleichseitigen Dreieck wie folgt lautet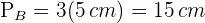 
2 Die Gesamtfläche ergibt sich aus der Summe der Seitenfläche und der doppelten Fläche der Grundfläche, d. h.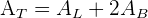 
. Wir berechnen die Seitenfläche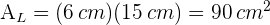 
3 Um die Höhe der Grundseite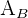 
zu berechnen, benötigen wir die Höhe 
des gleichseitigen Dreiecks. Diese erhalten wir mithilfe des Satzes des Pythagoras 
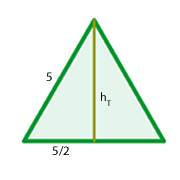
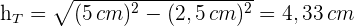
4 Wir berechnen die Fläche der Grundseite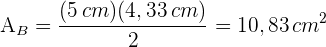 
5 Wir haben die Werte für die Seitenfläche und die Grundfläche, mit denen wir die Gesamtfläche berechnen können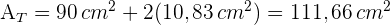 
6 Zuletzt berechnen wir das Volumen, das durch die Formel 
gegeben ist
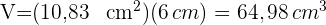
Maria schenkt ihrem Vater einen Bestseller zum Geburtstag. Sie wählt den Hardcover-Einband in Form eines rechteckigen Prismas mit den Maßen 18 cm Länge, 12 cm Breite und 6 cm Dicke. Wenn wir wissen, dass 10 % des Einbands von sich selbst verdeckt werden, wie groß ist dann die Fläche des verwendeten Geschenkpapiers?
Dieses Feld ist erforderlich.
1 Zunächst berechnen wir den Umfang der Grundfläche des Buches. Da diese ein Rechteck ist, müssen wir die Oberfläche des Buches berechnen Da das Buch ein rechteckiges Prisma ist, berechnen wir seine Gesamtfläche, wofür wir den Umfang der Grundfläche, die Seitenfläche und die Fläche der Grundfläche kennen müssen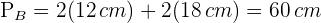 
2 Die Gesamtfläche ergibt sich aus der Summe der Seitenfläche und der doppelten Fläche der Grundfläche, d. h. 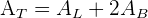. Wir berechnen die Seitenfläche 
3 Wir berechnen die Fläche der Grundfläche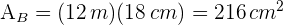 
4 Wir haben die Werte für die Seitenfläche und die Grundfläche, mit denen wir die Gesamtfläche berechnen können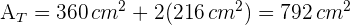 
5 Die Fläche des Buches beträgt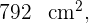 
, was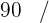 
%. Wir wenden den Dreisatz an und erhalten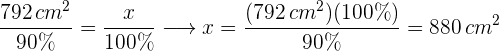 
Die Menge des verwendeten Papiers ist daher 
.
Volumen und Fläche der Pyramide
1
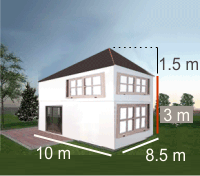
Berechne das Volumen des folgenden Hauses und die Fläche der Fassade.
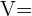
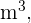
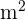
Dieses Feld ist erforderlich.
1 Das Volumen des Hauses ergibt sich aus der Addition des Volumens des Orthoeders und des Volumens der Pyramide. Wir berechnen die Fläche der Grundseite 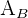der Pyramide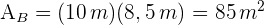 
2 Wir berechnen das Volumen 
der Pyramide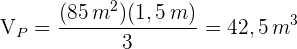 
3 Wir berechnen das Volumen des Orthoeders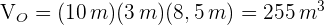 
4 Wir haben die Werte für das Volumen der Pyramide und das Volumen des Orthoeders, und wenn wir sie addieren, erhalten wir das Gesamtvolumen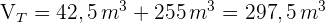 
5 Um die Fläche der Fassade zu berechnen, berechnen wir die Seitenfläche des Orthoeders
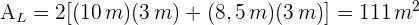
2
Berechne die Gesamtfläche, das Volumen und die Grundfläche einer fünfeckigen Pyramide von 7 cm Höhe, deren Grundfläche ein regelmäßiges Fünfeck mit einer Seitenlänge von 3 cm und einer Grundfläche von 2,6 cm ist. Runde auf zwei Dezimalstellen.
Dieses Feld ist erforderlich.
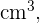
Dieses Feld ist erforderlich.
Dieses Feld ist erforderlich.
1 Wir wenden den Satz des Pythagoras an, um das Apothema der Pyramide zu berechnen und so die Gesamtfläche und das Volumen der Pyramide zu ermitteln.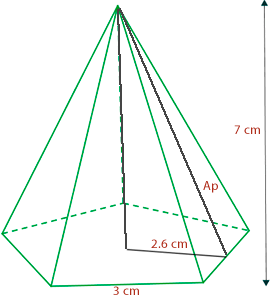 
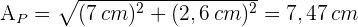
2 Um die Gesamtfläche zu erhalten, benötigen wir die Seitenfläche und die Fläche der Grundfläche. In beiden Fällen benötigen wir den Umfang der Grundfläche.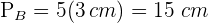
3 Da die Grundfläche ein Fünfeck ist, ist ihr Flächeninhalt die Hälfte des Produkts aus der Grundfläche und dem Umfang der Grundfläche.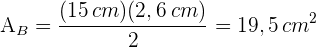
4 Die Seitenfläche wird durch Dreiecke gebildet, sodass ihre Fläche die Hälfte des Produkts aus dem Apothema der Pyramide und dem Umfang der Grundfläche ist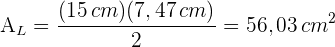
5 Die Gesamtfläche ist gleich der Summe aus der Seitenfläche und der Grundfläche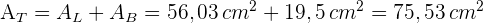
6Wir berechnen das Volumen, das ein Drittel des Produkts ausmacht.
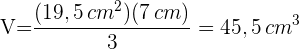
3
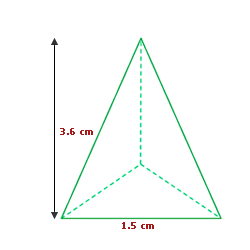
Eine dreieckige Pyramide, deren Grundfläche ein gleichseitiges Dreieck mit einer Seitenlänge von 1,5 cm ist, hat eine Höhe von 3,6 cm und das Apothema der Grundfläche misst 0,43 cm. Berechne das Volumen und die Gesamtfläche dieser Pyramide, gerundet auf zwei Dezimalstellen.
Dieses Feld ist erforderlich.
1 Um die Fläche und das Volumen zu berechnen, müssen wir zunächst das Apothema der Pyramide berechnen. Da wir das Apothema der Grundfläche und die Höhe kennen, wenden wir den Satz des Pythagoras an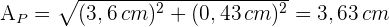 
2 Die Grundfläche ist ein gleichseitiges Dreieck. Um den Flächeninhalt zu ermitteln, brauchen wir also die Höhe.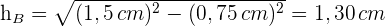 
3 Wir berechnen den Flächeninhalt der Grundfläche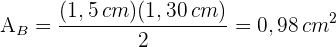 
4 Wir berechnen den Umfang der Grundseite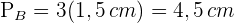 
5 Wir berechnen die Gesamtfläche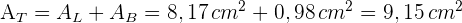 
6Wir berechnen das Volumen
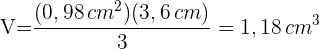
4
Die berühmten Pyramiden Ägyptens sind in der Regel viereckige Pyramiden. Die Cheopspyramide ist eine der berühmtesten. Wenn man ihre Maße annähert, kann man sagen, dass ihre Grundfläche ein Quadrat ist mit einer Seitenlänge von 230,35 m und einer Höhe von 146,61 m. Berechne das Volumen der Pyramide. Runde, falls nötig, auf zwei Dezimalstellen.
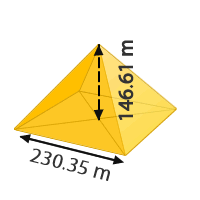
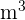
Wenn wir die Cheopspyramide mit einem Tuch bedecken wollten, wie viel Stoff würden wir dafür brauchen?
Dieses Feld ist erforderlich.
1 Da es sich um eine viereckige Pyramide handelt, misst das Apotheme des Quadrats die Hälfte der Seite, d. h.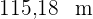 
2 Wir berechnen den Flächeninhalt der Grundfläche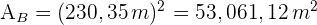 
3 Um die Seitenfläche zu ermitteln, benötigen wir den Umfang der Grundfläche und das Apothema der Pyramide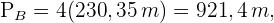 
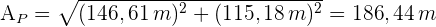
4 Wir berechnen die Seitenfläche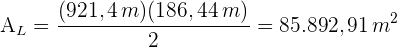 
5 Wir berechnen die Gesamtfläche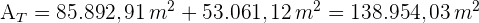 
6Wir berechnen das Volumen
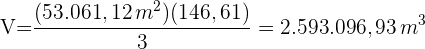
5
Berechne die Kante der Pyramide in der folgenden Abbildung.
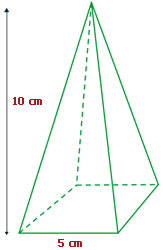
Dieses Feld ist erforderlich.
1 Zunächst berechnen wir die Diagonale des Quadrats mithilfe des Satzes des Pythagoras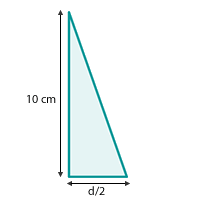 
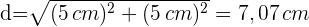
2 Zur Berechnung der Kante verwenden wir wieder den Satz des Pythagoras mit dem rechtwinkligen Dreieck, dessen Schenkel die Höhe der Pyramide und die Hälfte der Diagonale sind
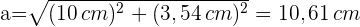
Volumen und Fläche des Pyramidenstumpfes
In Sandras Schreibtischschublade ist wenig Platz und sie möchte eine kleine Schachtel wie die auf dem Bild zur Aufbewahrung von Ohrringen verwenden. Wenn der Platz in der Schublade 12 cm breit, 10 cm tief und 11 cm hoch ist, passt die Box dann in die Schublade? Antworte mit Ja oder Nein.
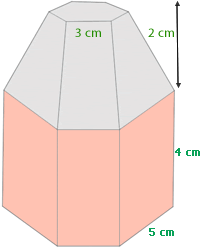
Wenn der Teil der pyramidenförmigen Schachtel der Teil ist, der dem Deckel entspricht, berechne die Menge an Stoff, die benötigt wird, um die Außenseite der Schachtel auszukleiden.
Dieses Feld ist erforderlich.
1 Wir berechnen das Volumen des freien Raums und das Volumen der Schachtel und vergleichen sie dann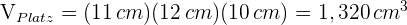 
2 Um das Volumen der Schachtel zu ermitteln, berechnen wir das Volumen des sechseckigen Prismas und addieren das Volumen des Pyramidenstumpfes. Dazu benötigen wir den Umfang und das Apothema der größeren Grundfläche.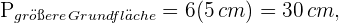 
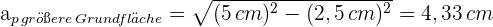
3 Wir berechnen die Fläche der größeren Grundfläche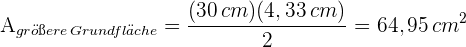 
4 Wir berechnen das Volumen des Prismas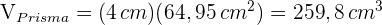 
5 Wir berechnen den Umfang und das Apothema der kleinen Grundfläche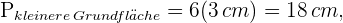 
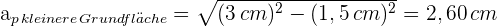
6 Wir berechnen die Fläche der kleinen Grundfläche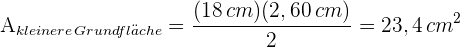 
7 Wir berechnen das Volumen des Pyramidenstumpfes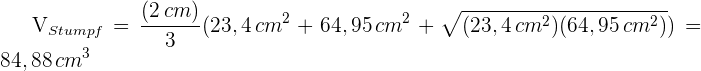 
8 Wir addieren das Volumen des Stumpfes und das Volumen des Prismas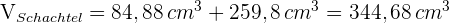 
Da das Volumen der Schachtel kleiner ist als das Volumen freien Platzes auf dem Schreibtisch, passt die kleine Schachtel hinein.
9 Um die benötigte Stoffmenge zu ermitteln, muss die Fläche des Pyramidenstumpfes berechnet werden. Daher muss die Fläche des Pyramidenstumpfes durch Anwendung des Satzes des Pythagoras auf das in der Zeichnung dargestellte Dreieck berechnet werden.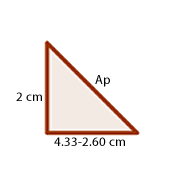 
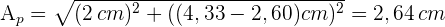
10 Mit den uns vorliegenden Werten können wir die Fläche berechnen, wobei wir nur die Seitenfläche des Deckels und den oberen Teil (Fläche der kleineren Grundfläche) benötigen
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
