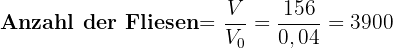Kapitel
Quader sind Parallelepipede, deren Flächen alle rechtwinklig sind.
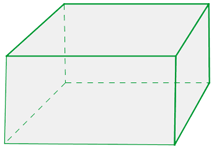
Bildung eines Quaders
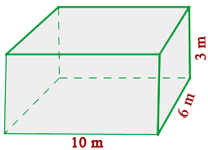
Zur Bildung eines Quaders sehen wir uns folgende Zeichnung an. Diese zeigt alle Seiten des Quaders, die durch Verdoppelung seiner Kanten den Körper ergeben.
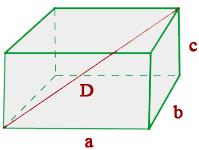
Formel zur Berechnung der Diagonale eines Quaders
Wie in der dritten Abbildung zu sehen ist, umfasst die Diagonale die drei Kanten und wird mit Hilfe des Satzes des Pythagoras berechnet.
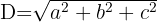
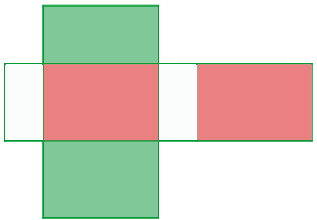
Fläche eines Quaders
Die zweite Abbildung zeigt die Seitenflächen, bei denen es sich um drei Paare von Rechtecken handelt, deren Fläche sich aus Grundfläche mal Höhe ergibt; die dritte Abbildung zeigt die Fläche:
Volumen eines Quaders
Das Volumen wird wie folgt berechnet: Länge mal Breite mal Höhe.
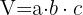
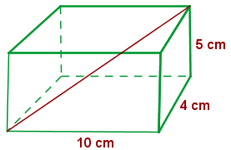
Aufgaben zur Berechnung der Diagonale, der Fläche und des Volumens eines Quaders
Berechne die Diagonale eines Quaders mit einer Länge von 
, einer Breite von 
und einer Höhe von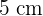 
.
Wir haben 
und 
. Also setzen wir in die Formel ein und erhalten: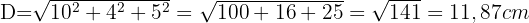 
Berechne das Volumen eines Raumes in Kubikzentimetern, der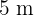 
lang, 
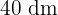breit und 
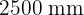hoch ist.
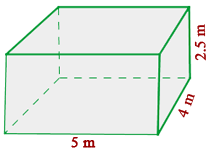
Zuerst rechnen wir in Kubikmetern, dann wechseln wir zu Kubikzentimetern. Wir erhalten die Länge:
danach die Breite
und schließlich die Höhe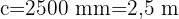
nun setzen wir in die Formel ein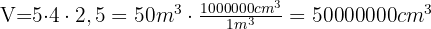
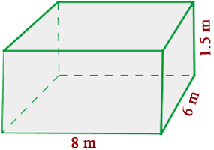
Ein Schwimmbecken ist 
lang, 
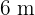breit und 
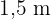tief. Der Anstrich des Schwimmbeckens kostet 
€ pro Quadratmeter. Wie viel kostet der Anstrich? Wie viele Liter Wasser werden benötigt, um das Becken zu füllen?
Um herauszufinden, wie viel der Anstrich kosten wird, müssen wir die Fläche des Schwimmbeckens abzüglich der Oberseite berechnen, also lautet die Formel: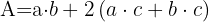 
,
wobei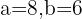
und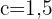 
. Wir setzen in die Formel ein
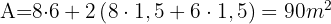Die Kosten betragen somit
€. Um herauszufinden, wie viele Liter benötigt werden, berechnet man das Volumen, indem man in die Formel die gegebenen Werte einsetzt: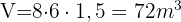 
und da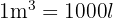 
, ist
In einem Lagerraum mit einer Länge von 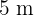, einer Breite von 
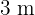und einer Höhe von 
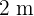sollen Kisten mit einer Länge von 
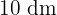, einer Breite von 
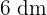und einer Höhe von 
gelagert werden. Wie viele Kisten können gelagert werden?
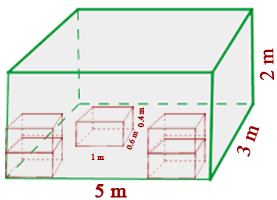
Zunächst berechnen wir das Volumen des Lagers: Die Länge ist , die Breite ist 
und die Höhe ist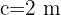 
, dann setzen wir in die Formel ein. Wir erhalten:
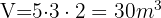. Wir berechnen nun das Volumen einer Kiste und nennen es daher 
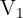, um Verwirrung zu vermeiden: Die Länge ist 
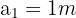, die Breite ist 
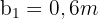und die Höhe ist 
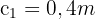. Wir setzen in die Formel ein und erhalten: 
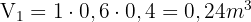. Schließlich berechnen wir die Anzahl der Kisten und die Formel lautet: 
.
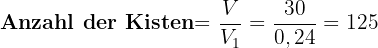Wie viele quadratische Fliesen von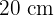 
werden benötigt, um die Seiten eines Schwimmbeckens von 
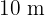Länge, 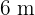Breite und 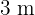Tiefe zu fliesen?
Zuerst berechnen wir die Fläche des Beckens abzüglich der Oberseite. Die Formel lautet: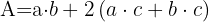
, wobei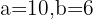
und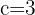 
. Nun setzen wir in die Formel ein
Wir berechnen die Fläche einer Fliese und da die Fliesen quadratisch sind, erhalten wir: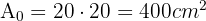
Wir rechnen in Quadratmeter um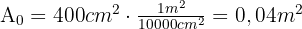
Schließlich berechnen wir die Anzahl der Fliesen, indem wir die Fläche des Beckens durch die Fläche der Fliese teilen
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
