Merkmale eines Zylinders
Ein rechtwinkliger Zylinder setzt sich aus verschiedenen Teilen zusammen, wie folgt
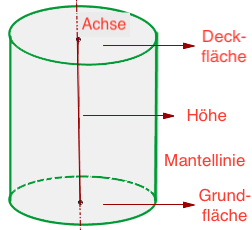
Zylinderböden: Deckfläche & Grundfläche
Dies sind die Kreise, die den unteren und oberen Rand des Zylinders bilden. Die Deckfläche und die Grundfläche sind gleich und parallel.
Zylinderachse
Sie ist die Achse, die durch die Mittelpunkte der Grundflächen des Zylinders verläuft; sie steht senkrecht zu diesen Grundflächen. Beachte, dass die Achse die Seite des Rechtecks enthält, die sich um sich selbst dreht.
Höhe
Sie ist die Länge des Segments, dessen Enden die Mittelpunkte der beiden Basen sind. Sie ist gleich der Seite des Rechtecks, die sich um sich selbst dreht.
Mantellinie
Sie ist die der Höhe gegenüberliegende Seite und ist die Seite, die den Zylinder erzeugt. Beachte, dass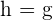 
Mantelfläche des Zylinders
Sie ist gleich der Fläche des Zylinders ohne Berücksichtigung der Fläche seiner Kreisflächen
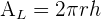
Flächeninhalt des Zylinders
Sie ist gleich der Gesamtoberfläche des Zylinders unter Berücksichtigung seiner Kreisflächen
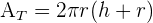
Volumen des Zylinders
Übungsaufgaben
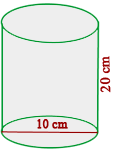
1Berechne die Menge an Blech, die benötigt wird, um 
zylindrische Dosen 
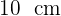im Durchmesser und 
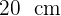Höhe herzustellen.
1Die Menge des benötigten Blechs entspricht der Gesamtfläche des Zylinders
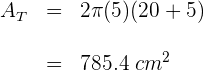
2Die Gesamtmenge an Blech, die zur Herstellung von Dosen benötigt wird, beträgt
2Die Höhe des Zylinders ist gleich lang wie der Umfang der Basis. Wenn die Höhe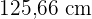 
beträgt. Berechne die Gesamtfläche und das Volumen.
1Nutze zunächst die Tatsache, dass die Höhe gleich der Länge des Umfangs der Basis ist, um den Wert des Radius zu finden
2Berechne die Gesamtfläche
3Berechne das Volumen
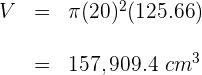
3In einen Messzylinder mit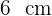 
Radius werden vier Eiswürfel mit 
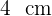Rand gefüllt. Wie hoch wird das Wasser steigen, wenn sie schmelzen?
1Berechne das Volumen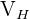 
eines Eiswürfels
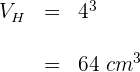
Das von den vier Eiswürfeln eingenommene Volumen ist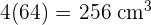 
2Setze um die Höhe des Messzylinders zu ermitteln das Volumen des Zylinders 
mit dem Wasservolumen in den vier Würfeln gleich
4Ein zylindrischer Behälter mit 10 cm Radius und 5 cm Höhe ist mit Wasser gefüllt. Wenn die Masse des vollen Behälters 2 kg beträgt, wie groß ist dann die Masse des leeren Behälters?
1Berechne das Volumen des Behälters
2Es ist bekannt, dass ein 
gleich einem 
ist, rechne daher das Volumen in um
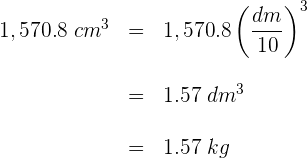
3Die Masse des leeren Behälters ist also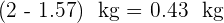 
5Wenn der Radius der Grundfläche eines Zylinders halbiert wird, ist dann sein Volumen gleich der Hälfte des ursprünglichen Volumens?
1Berechne das Volumen des Zylinders mit Radius 
und Höhe 
2Berechne das Volumen für den Zylinder mit halbiertem Radius
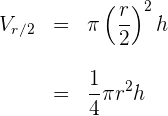
3Das Volumen des Zylinders mit dem halbierten Radius ist gleich einem Viertel des Volumens des ursprünglichen Zylinders, nicht der Hälfte davon.
6Du willst eine zylindrische Dose bauen, deren Radius ein Viertel ihrer Höhe beträgt. Drücke das Volumen und die Gesamtfläche der Dose in Abhängigkeit vom Radius der Dose aus.
1Berechne das Volumen des Zylinders mit Radius und Höhe
2Verwende die Tatsache, dass der Radius gleich einem Viertel der Höhe ist, um die Höhe in Bezug auf den Radius auszudrücken
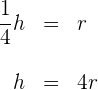
3Setze den Wert in die Volumenformel ein, um ihn in Bezug auf auszudrücken
4Setze den Wert in die Formel für die Gesamtfläche ein, um sie in Form von auszudrücken
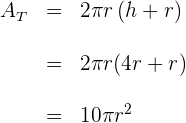
7Die Höhe eines Zylinders nimmt um 
Einheiten zu. Wie groß ist die Zunahme seines Volumens?
1Berechne das Volumen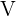 
des Zylinders mit Radius und Höhe
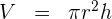
2Berechne das Volumen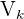 
des Zylinders mit der Zunahme von Einheiten in seiner Höhe
Das Volumen vergrößert sich um das 
-fache der Fläche seiner Grundfläche
8Wie groß ist das Volumen eines Zylinders der Höhe 
, der in eine Kugel mit Radius eingeschrieben ist?
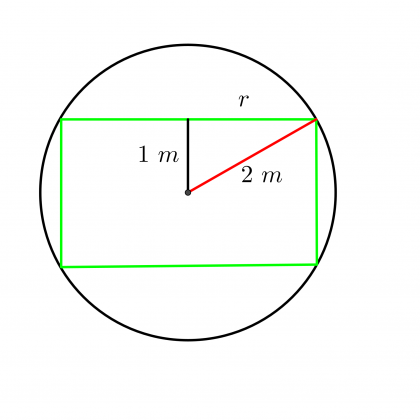
1Berechne den Radius des Zylinders, der in die Kugel mit dem Radius eingeschrieben ist, mit Hilfe des Satzes von Pythagoras
2Berechne das Volumen 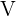des Zylinders
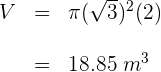
9Ein Betonzylinder mit dem Durchmesser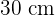 
, der Dicke 
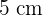und der Höhe 
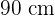wird konstruiert. Wie groß ist das Volumen des Betons, der zum Bau des Zylinders verwendet wurde?
1Berechne das Volumen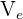 
des äußeren Zylinders mit Durchmesser 
und Höhe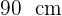 
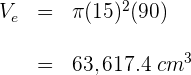
2Berechne das Volumen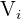 
des inneren Zylinders mit Durchmesser 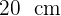und Höhe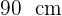
3Die Menge 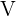des verwendeten Betons beträgt
.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
