Aufgabenstellung
Ein Warenhaus bestellt Sporthosen und-jacken bei einem Hersteller. Der Hersteller verfügt für die Produktion über 750 m Baumwollstoff und 1000 m Polyesterstoff. Für die Herstellung jeder Hose benötigt er 1 m Baumwollstoff und 2 m Polyesterstoff; für jede Jacke 1.5 m Baumwollstoff und 1 m Polyesterstoff. Eine Hose soll im Verkauf 50 € kosten, eine Jacke 40 €.
¿Wie viele Hosen und Jacken muss der Hersteller liefern, damit das Warenhaus den größtmöglichen Gewinn erzielt?
Lösung:
1 Definiere die Unbekannten
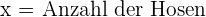
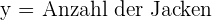
2 Zielfunktion
3 Restriktionen
Um die Restriktionen zu definieren, stellt man alle Werte in einer Tabelle dar:
| Hosen | Jacken | verfügbar | |
|---|---|---|---|
| Baumwollstoff |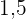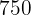 
| 
| 
|
| Polyesterstoff | 
|
| 
|
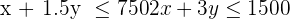
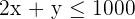
Da die Anzahl der Hosen und Jacken mit natürlichen Zahlen angegeben werden, gibt es außerdem die folgenden beiden Restriktionen:
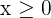
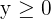
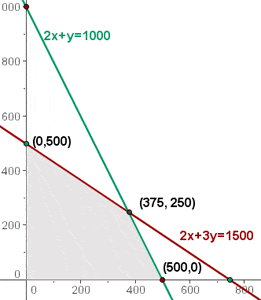
4 Finde die Menge der realisierbare Lösungen. Stelle dazu die Restriktionen grafisch dar.
Da 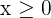ist und 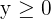, schaut man sich nur den ersten Quadranten an.
Zeichne die Geraden in das Koordinatensystem mit den Schnittpunkten auf der jeweiligen Achse ein.
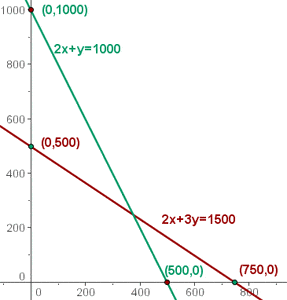
Löse die Ungleichung mit der grafischen Methode: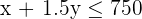 
Wähle dafür einen Punkt auf der Ebene, zum Beispiel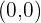 
.
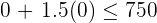
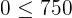
Der Punkt 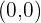befindet sich also auf der Halbebene, für die die Ungleichung Lösungswerte besitzt.
Löse analog dazu .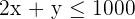
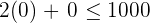
Die Zone, in der sich die Lösungen der Ungleichungen schneiden, stellt die zulässige Lösungsmenge dar.
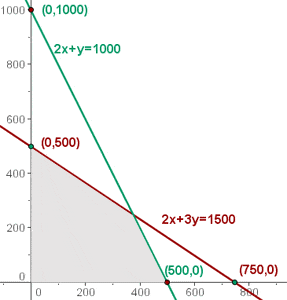
5 Ermittle nun, welche Koordinaten die Eckpunkte des zulässigen Lösungsbereichs haben.
Wenn es nur eine Optimallösung gibt, befindet sich diese an einem Eckpunkt. Dies sind die Lösungen des Systems:
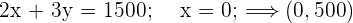
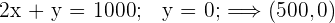
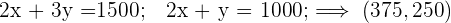
6 Berechne nun den Wert der Zielfunktion
Setze die Werte jedes Eckpunkts in die Zielfunktion ein.
€
€
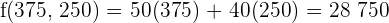€, d.h. man erhält einen Maximalwert.
Die Optimallösung ist es, 375 Hosen und 250 Jacken herzustellen, um einen Gewinn von 28750 € zu erzielen.
Nicht immer gibt es eine einzige optimale Lösung.
Wenn die Zielfunktion des Rechenbeispiels folgende gewesen wäre:
€ (Maximum)
€
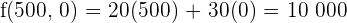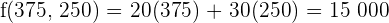€ (Maximum)
In diesem Fall wären alle ganzen Zahlen, die sich auf der schwarz eingezeichneten Geraden befinden, Maximalwerte.
€
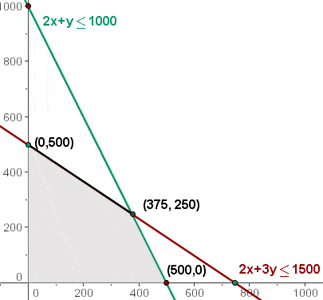
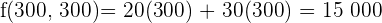Die Plattform, die Lehrer/innen und Schüler/innen miteinander verbindet
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
