Kapitel
Die lineare Optimierung, auch lineare Programmierung genannt, wird zur Maximierung oder Minimierung linearer Funktionen angewandt. Die Funktionen unterliegen dabei bestimmten Nebenbedingungen, die als Restriktionen bezeichnet werden. Die zu maximierende Funktion wird als Zielfunktion bezeichnet.
Lineare Optimierung dient der Ermittlung einer oder mehrerer optimaler Lösungen und findet in vielfältigen Einsatzbereichen Anwendung, besonders in der Produktion und der Logistik.
Die Zielfunktion
Lineare Optimierung besteht im Grunde darin, eine Zielfunktion, das heißt eine lineare Funktion mit mehreren Variablen, zu minimieren oder zu maximieren, um die Optimallösung(en) zu finden:
Die Nebenbedingungen (Restriktionen)
Die Zielfunktion unterliegt einer Reihe von Restriktionen, die durch lineare Ungleichungen ausgedrückt werden:
 |
 |
| ... ... ... |
 |
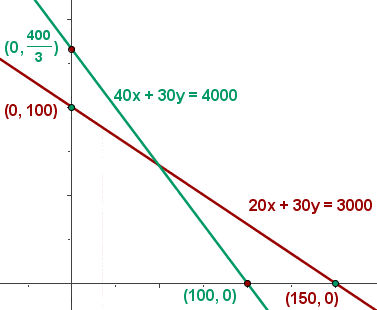
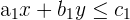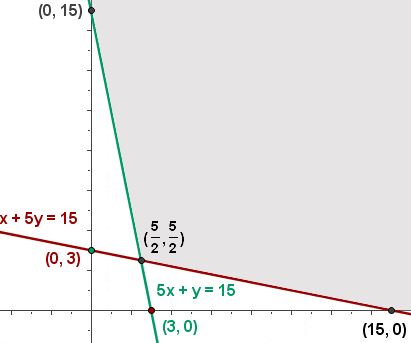
Anhand der Nebenbedingungen ergeben sich Halbebenen im Koordinatensystem.
Die zulässige Menge
Die Schnittpunkte aller durch die Restriktionen gebildeten Halbebenen bestimmen zusammen mit den Achsen des ersten Quadranten des Koordinatensystems einen unbeschränkten oder beschränkten Bereich, in dem sich alle möglichen Lösungen befinden, die sogenannte zulässige Menge.
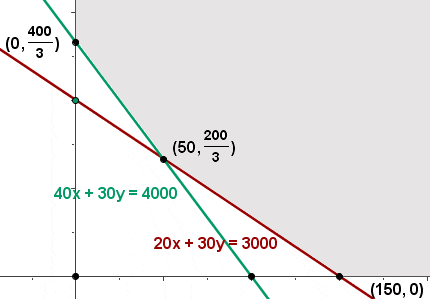
Die Optimallösung
Die Menge, die durch der Eckpunkte des Bereichs der Optimallösungen festgelegt wird, wird mögliche Lösungsmenge genannt. Der Punkt, der die Optimallösung darstellt, wird als Maximal- bzw. Minimallösung bezeichnet.
Wert des linearen Programms
Der Wert, den die Zielfunktion im Bereich der Optimallösungen einnimmt, nennt sich Wert des linearen Programms.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
