Optimierung der Produktion in einer Lampenfabrik
Ein Unternehmen stellt zwei Arten von Lampen, Modell L1 und Modell L2, her und vertreibt diese.
Für die Herstellung von Modell L1 ist manuelle Arbeit von 20 Minuten, für Modell L2 von 30 Minuten nötig; für Modell L1 werden 20 Minuten maschinelle Arbeit benötigt, für Modell L2 10 Minuten.
Das Unternehmen verfügt über Arbeitskraft für 100 Stunden manuelle Arbeit und 80 Stunden maschinelle Arbeit pro Monat. Der Gewinn pro verkaufter Lampe beträgt 15€ für Modell L1 und 10€ für Modell L2.
Unter welchen Bedingungen wird der höchste Gewinn erzielt?
Ein Unternehmen stellt zwei Arten von Lampen, Modell L1 und L2, her und vertreibt diese.
Für die Herstellung von Modell L1 ist manuelle Arbeit von 20 Minuten, für Modell L2 von 30 Minuten nötig; für Modell L1 werden 20 Minuten maschinelle Arbeit benötigt, für Modell L2 10 Minuten.
Das Unternehmen verfügt über Arbeitskraft für 100 Stunden manuelle Arbeit und 80 Stunden maschinelle Arbeit pro Monat. Der Gewinn pro verkaufter Lampe beträgt 15€ für Modell L1 und 10€ für Modell L2.Unter welchen Bedingungen wird der höchste Gewinn erzielt?
1
x = Anzahl der Lampen des Modells L1
y = Anzahl der Lampen des Modells L2
2
f(x, y) = 15x + 10y
3
Rechne die Zeitangaben in Stunden um
20 min = 1/3 h
30 min = 1/2 h
10 min = 1/6 h
Um die Restriktionen zu definieren, stellt man alle Werte in einer Tabelle dar:
| L1 | L2 | Benötigte Zeit | |
|---|---|---|---|
| Manuelle Arbeit | 1/3 | 1/2 | 100 |
| Maschinelle Arbeit | 1/3 | 1/6 | 80 |
1/3x + 1/2y ≤ 100
1/3x + 1/6y ≤ 80
Da die Anzahl der Lampen mit natürlichen Zahlen angegeben wird, gelten außerdem die folgenden Restriktionen:
x ≥ 0
y ≥ 0
4
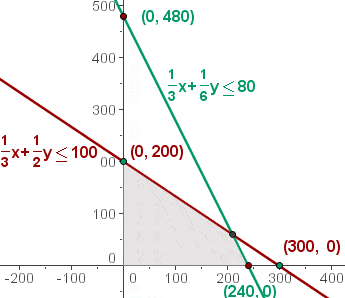
Stelle die Restriktionen dazu grafisch dar.
Da x ≥ 0 und y ≥ 0 schaut man sich nur den ersten Quadranten an.
Zeichne die Geraden in das Koordinatensystem mit den Schnittpunkten auf der jeweiligen Achse ein.
Löse die Ungleichung mit der grafischen Methode: 1/3 x + 1/2 y ≤ 100; Wähle dafür einen Punkt auf der Ebene, zum Beispiel (0,0).
1/3·0 + 1/2·0 ≤ 100
1/3·0 + 1/6·0 ≤ 80
Die Zone, in der sich die Lösungen der Ungleichungen schneiden, stellt die zulässige Lösungsmenge dar.
5
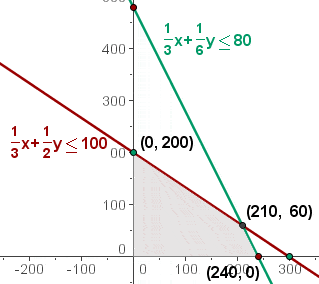
Wenn es nur eine Optimallösung gibt, befindet sich diese an einem Eckpunkt. Dies sind die Lösungen des Systems:
1/3x + 1/2y = 100; x = 0 (0, 200)
1/3x + 1/6y = 80; y = 0(240, 0)
1/3x + 1/2y = 100; 1/3x + 1/6y = 80(210, 60)
6
Setze die Werte jedes Eckpunkts in die Zielfunktion ein.
f(x, y) = 15x + 10y
f(0, 200) = 15·0 + 10·200 = 2 000 €
f(240, 0 ) = 15·240 + 10·0 = 3 600 €
f(210, 60) = 15·210 + 10·60 = 3 750 € (Maximum)
Die Optimallösung ist es, 210 Lampen des Modells L1 und 60 Lampen des Modells L1 herzustellen, um einen Gewinn von 3 750 € zu erzielen.
Optimierung beim Verkauf von Schulmaterialien
Zu Beginn des neuen Schuljahrs sind Schulmaterialien im Angebot.
Ein Warenhaus möchte 600 Schulhefte, 500 Schulordner und 400 Kugelschreiber in Form von zwei unterschiedlichen Sets anbieten:
Das erste Set enthält 2 Schulhefte, 1 Ordner und 2 Kugelschreiber; das zweite enthält 3 Schulhefte, 1 Ordner und 1 Kugelschreiber.
Set 1 soll im Verkauf für 6,50€, Set 2 für 7€ erhältlich sein.
Wie viele Sets jeder Art sollten hergestellt werden, um den höchsten Gewinn zu erzielen?
Zu Beginn des neuen Schuljahrs sind Schulmaterialien im Angebot.
Ein Warenhaus möchte 600 Schulhefte, 500 Schulordner und 400 Kugelschreiber in Form von zwei unterschiedlichen Sets anbieten:
Das erste Set enthält 2 Schulhefte, 1 Ordner und 2 Kugelschreiber; das zweite enthält 3 Schulhefte, 1 Ordner und 1 Kugelschreiber.
Set 1 soll im Verkauf für 6,50€, Set 2 für 7€ erhältlich sein.
Wie viele Sets jeder Art sollten hergestellt werden, um den höchsten Gewinn zu erzielen?
1
x = P1
y = P2
2
f(x, y) = 6.5x + 7y
3
P1
P2
Verfügbarkeit
Schulhefte
2
3
600
Schulordner
1
1
500
Kugelschreiber
2
1
400
2x + 3y ≤ 600
x + y ≤ 500
2x + y ≤ 400
x ≥ 0
y ≥ 0
4
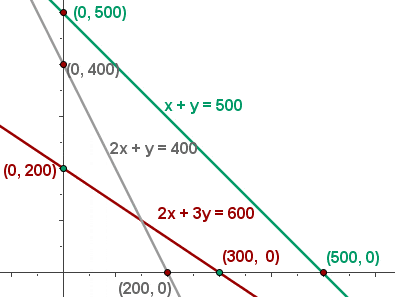
5
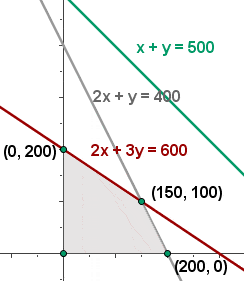
6
f(x,y) = 6.5 · 200 + 7 · 0 = 1300 €
f(x,y)= 6.5 · 0 + 7 · 200 = 1 400 €
f(x,y)= 6.5 · 150 + 7 · 100 = 1 675 € , d.h. man erhält einen Maximalwert.
Die Optimallösung ist es, 150 P1 und 100 P2 zu vertreiben, um einen Gewinn von 1 675 € zu erzielen.
Optimierung der Fütterung auf einer Farm
Auf einer Hühnerfarm wird den Tieren Futter für eine schnelle Gewichtszunahme verabreicht, das sich zu mindestens 15 Einheiten eines Nährstoffes A und 15 eines Nährstoffes B zusammensetzt.
Auf dem Markt angeboten werden zwei Arten von Futter: Futter X mit einer Zusammensetzung von einer Einheit des Nährstoffes A und 5 des Nährstoffes B; und Futter Y mit einer Zusammensetzung von 5 Einheiten des Nährstoffes A und einer Einheit des Nährstoffes B. Futter X kostet 10€ und Futter Y 30€.
Wie viel muss von jedem Futter gekauft werden, um den Bedarf zum geringsten Preis abzudecken?
1
x = X
y = Y
2
f(x,y) = 10x + 30y
3
X
Y
Minimum
A
1
5
15
B
5
1
15
x + 5y ≥ 15
5x + y ≥ 15
x ≥ 0
y ≥ 0
4
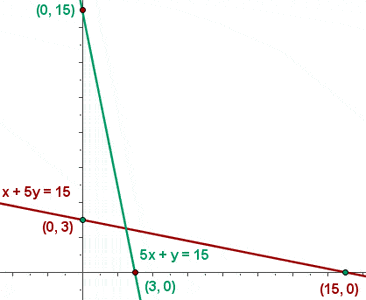
5
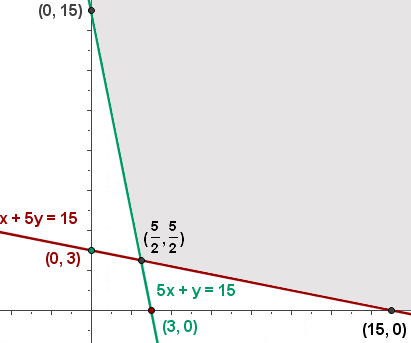
6
f(0, 15) = 10 · 0 + 30 · 15 = 450
f(15, 0) = 10 · 15 + 30 · 0 = 150
f(5/2, 5/2) = 10 · 5/2 + 30 · 5/2 = 100 (Minimum)
Die geringsten Kosten liegen bei 100 € für X = 5/2 und Y = 5/2.
1
Optimierung bei der Herstellung von Medizinprodukten
Ein medizinischer Hersteller verfügt über 600 g eines Arzneimittels, um große und kleine Tabletten zu produzieren. Die großen sollen 40 g wiegen, die kleinen 30 g.
Für die Packung großer Tabletten werden mindestens drei Tabletten benötigt, für die Packung kleine Tabletten mindestens doppelt so viele. Jede Tablette bringt einen Gewinn von 2€ (große Tabletten) und 1€ (kleine Tabletten) ein.
Wie viele Tabletten müssen jeweils hergestellt werden, um den maximalen Gewinn zu erzielen?
1 Definiere die Unbekannten.
x = Anzahl der großen Tabletten
y = Anzahl der kleinen Tabletten
2 Zielfunktion
f(x, y) = 2x + y
3 Restriktionen
40x + 30y ≤ 600
x ≥ 3
y ≥ 2x
x ≥ 0
y ≥ 0
4 Finde die Menge der realisierbaren Lösungen.
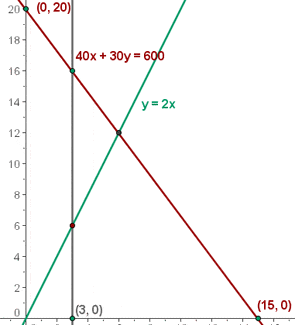
5
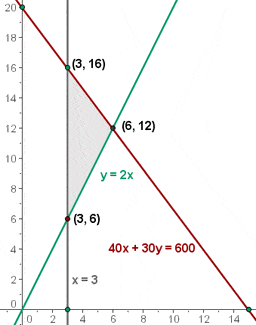
6
f(x, y) = 2 · 3 + 16 = 22 €
f(x, y) = 2 · 3 + 6 = 12 €
f(x, y) = 2 · 6 + 12 = 24 € (Maximum)
Der höchste Gewinn von 24 € wird dann erzielt, wenn 6 große Tabletten und 12 kleine hergestellt werden.
Optimierung beim Schlussverkauf im Kleiderhandel
Ein Kaufhaus möchte 200 Hemden und 100 Hosen der vorherigen Saison zu Sonderpreisen anbieten.
Dafür werden die Angebot A und B entworfen.
Angebot A enthält ein Set aus einem Hemd und einer Hose, das für 30€ verkauft werden soll. Angebot B enthält ein Set aus drei Hemden und einer Hose und soll 50€ kosten. Es sollen mindestens 20 Sets für Angebot A und 10 Sets für Angebot B vorbereitet werden.
Wie viele Sets jeder Art müssen verkauft werden, um den maximalen Gewinn zu erzielen?
1
x = Anzahl des Sets A
y = Anzahl des Sets B
2
f(x, y) = 30x + 50y
3
A
B
Minimum
Hemden
1
3
200
Hosen
1
1
100
x + 3y ≤ 200
x + y ≤ 100
x ≥ 20
y ≥ 10
4
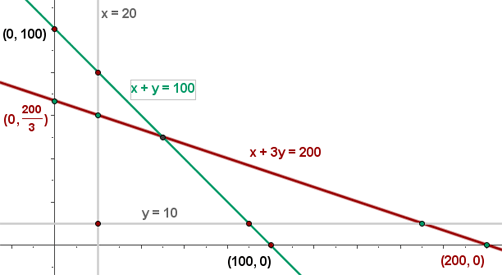
5
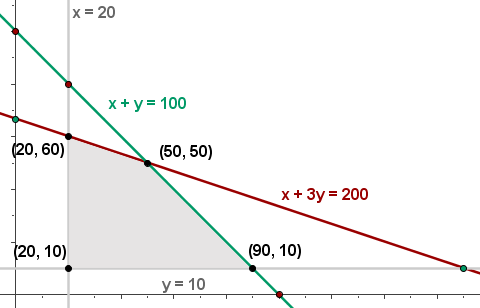
6
f(x, y) = 30 · 20 + 50 · 10 = 1100 €
f(x, y) = 30 · 90 + 50 · 10 = 3200 €
f(x, y) = 30 · 20 + 50 · 60 = 3600 €
f(x, y) = 30 · 50 + 50 · 50 = 4000 € (Maximum)
Der maximale Gewinn von 4000 € wird erzielt, wenn man jeweils 50 der beiden Sets verkauft.



