Berechnung des Maximalgewinns:
Ein Kaufhaus beauftragt einen Hersteller mit der Produktion von Sporthosen und -jacken. Der Hersteller disponiert für die Produktion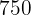 
m Baumwolle und 
m Polyester. Für jede Hose werden 
m Baumwolle und 
m Polyester benötigt. Für jede Jacke werden 
m Baumwolle und m Polyester benötigt. Der Preis der Hose liegt bei 
€ und der Preis der Jacke bei 
€. Wie viele Hosen und Jacken muss der Hersteller an das Kaufhaus liefern, damit er einen maximalen Gewinn erzielen kann?
1 Auswahl der Unbekannten.
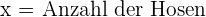
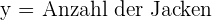
2 Zielfunktion
3 Einschränkungen
Um die Einschränkungen festzulegen, nutzen wir eine Tabelle:
| Hosen | Jacken | verfügbar | |
|---|---|---|---|
| Baumwolle | 1 | 1,5 | 750 |
| Polyester | 2 | 1 | 1000 |
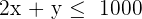
Da es sich bei der Anzahl der Hosen und Jacken um natürliche Zahlen handelt, haben wir zwei weitere Einschränkungen:
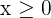
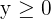
4 Wir bestimmen die Gesamtheit der durchführbaren Lösungen
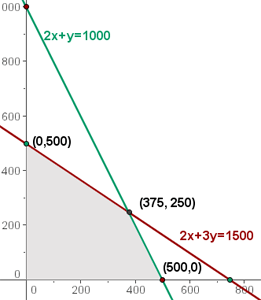
Wir müssen die Einschränkungen graphisch darstellen.
Da 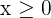und 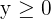, nehmen wir uns den ersten Quadranten vor.
Wir stellen die Geraden ausgehend von ihren Schnittpunkten mit den Achsen dar.
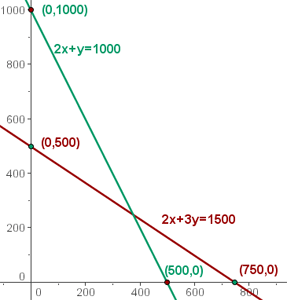
Wir lösen die Ungleichung graphisch: 
; dafür nehmen wir einen Punkt auf der Ebene, zum Beispiel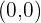 
.
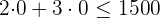
Da 
, befindet sich der Punkt 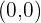in der Halbebene an dem Punkt, an dem die Ungleichheit erfüllt ist.
Analog dazu lösen wir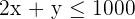 
.
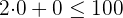
Der Schnittbereich der Lösungen der Ungleichungen ist die Lösung für das Ungleichungssystem, das die Gesamtheit der durchführbaren Lösungen bildet.
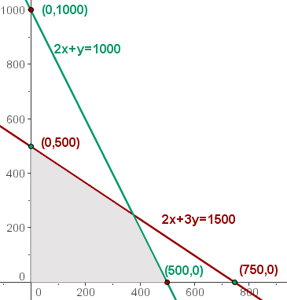
5 Wir berechnen die Koordinaten der Scheitelpunkte des Bereichs der durchführbaren Lösungen.
Die optimale Lösung, falls sie eindeutig ist, befindet sich an einem Scheitelpunkt des Bereichs; diese sind die Lösungen für die Systeme:
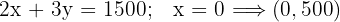
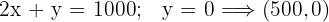
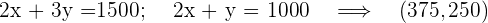
6 Wir berechnen den Wert der Zielfunktion, für den wir in der Zielfunktion jeden einzelnen der Scheitelpunkte ersetzen
€
€
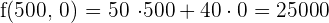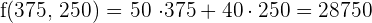€ Maximum
Die optimale Lösung ist die Produktion von 
Hosen und 
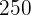Jacken, um einen Gewinn von 
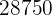€ zu erzielen.
Berechnung des Maximalgewinns:
Ein Unternehmen produziert und verkauft zwei Modelle von Lampen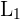 
und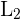 
. Für deren Herstellung werden für das Modell 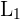20 Minuten manuelle Arbeit und 
Minuten manuelle Arbeit für das Modell 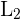benötigt; für 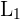fallen 10 Minuten und für 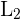20 Minuten maschinelle Arbeit an. Pro Monat fallen für die manuelle Arbeit 
und für die maschinelle Arbeit 
Stunden an. Da der Gewinn pro Einheit bei 
und 
Euro für 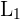und 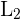liegt, muss die Produktion entsprechend geplant werden, um den Maximalgewinn zu erzielen.
1 Auswahl der Unbekannten.
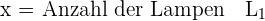
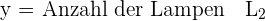
2 Zielfunktion
3 Einschränkungen
Wir geben die Zeiten in Stunden an
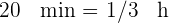
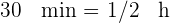
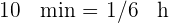
Um die Einschränkungen zu beschreiben, nutzen wir eine Tabelle:
| L1 | L2 | Zeit | |
|---|---|---|---|
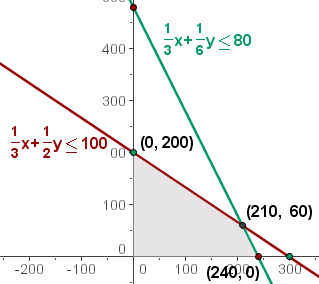
| Manuell | 1/3 | 1/2 | 100 |
| Maschinell | 1/3 | 1/6 | 80 |
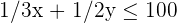
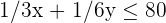
Da die Anzahl der Lampen natürliche Zahlen sind, haben wir zwei weitere Einschränkungen:
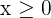
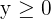
4 Wir bestimmen die Gesamtheit der durchführbaren Lösungen
Wir müssen die Einschränkungen graphisch darstellen.
Da 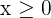und 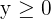, nehmen wir uns den ersten Quadranten vor.
Wir stellen die Geraden ausgehend von ihren Schnittpunkten mit den Achsen dar.
Wir lösen die Gleichung graphisch: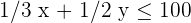 
; dazu nehmen wir einen Punkt in der Ebene, zum Beispiel 
.
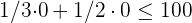
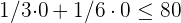
Der Schnittbereich der Lösungen der Ungleichungen ist die Lösung für das Ungleichungssystem, das die Gesamtheit der durchführbaren Lösungen bildet.
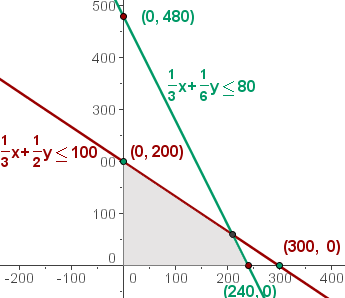
5 Wir berechnen die Koordinaten der Scheitelpunkte des Bereichs der durchführbaren Lösungen.
Die optimale Lösung, wenn sie eindeutig ist, befindet sich an einem Scheitelpunkt des Bereichs. Diese sind die Lösungen der Systeme:
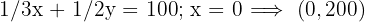
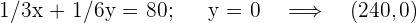
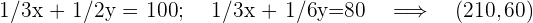
6 Wir berechnen den Wert der Zielfunktion
Wir ersetzen in der Zielfunktion jeden einzelnen der Scheitelpunkte.
€
€
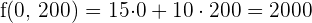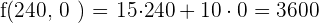€ Maximum
Die optimale Lösung ist die Herstellung von 210 Stücken von Modell 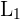und 60 von Modell 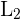, um einen Gewinn von 
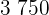€ zu erzielen.
Rechenaufgabe zur Kostenminimalisierung
Ein Transportunternehmen hat zwei Typen von LKW. Typ 
mit einem gekühlten Bereich von 
m³ und einem ungekühlten Bereich von m³. Typ 
hat das gleiche Gesamtfassungsvermögen, mit einem Anteil an gekühltem und ungekühltem Bereich von %. Das Unternehmen wird beauftragt, einen Transport von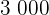 
m³ eines Produkts, das gekühlt werden muss und 
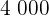m³ eines anderen Produkts, das keine Kühlung benötigt, durchzuführen. Der Preis pro Kilometer mit einem LKW vom Typ beträgt € und mit einem LKW vom Typ €. Wie viele LKW von jedem Typ müssen eingesetzt werden, damit die Gesamtkosten minimal bleiben?
1 Auswahl der Unbekannten.
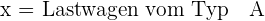
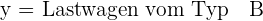
2 Zielfunktion
3 Bedingungen
| A | B | Gesamt | |
|---|---|---|---|
| Gekühlt | 20 | 30 | 3000 |
| Ungekühlt | 40 | 30 | 4000 |
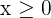
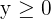
4 Wir bestimmen die Gesamtheit der durchführbaren Lösungen
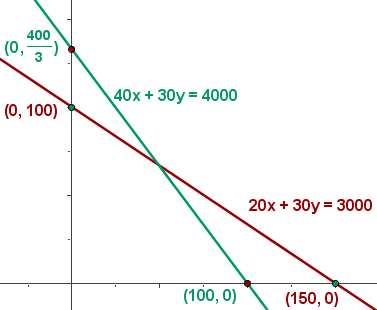
5 Wir berechnen die Koordinaten der Scheitelpunkte des Bereichs der durchführbaren Lösungen.
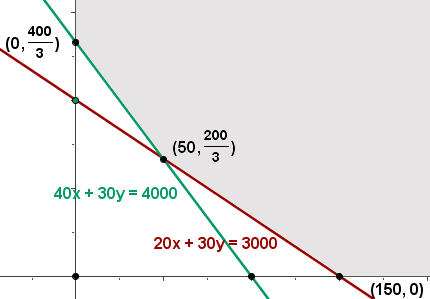
6 Wir berechnen den Wert der Zielfunktion
Da 
und 
natürliche Zahlen sein müssen, runden wird den Wert für .
Wir sehen nun, welchen Wert für 
in der Gleichung 
einnimmt, der zum Bereich der durchführbaren Lösungen gehört; 
. Wir erhalten eine natürliche Zahl
Die Minimalkosten liegen bei 
€ für 
und 
Decken von Mindestausgaben berechnen
Auf einer Hühnerfarm soll das Futter der Hühner umgestellt werden, damit diese schneller wachsen. Sie erhalten eine Mischung aus Einheiten einer Substanz und weitere Einheiten einer anderen Substanz . Auf dem Markt sind nur zwei Arten von Zusammensetzungen erhältlich: Typ 
mit einer Zusammensetzung aus einer Einheit von und 
von . Der andere Typ, 
, ist eine Zusammensetzung aus fünf Einheiten von und einer Einheit von . Der Preis für Typ liegt bei Euro und für Typ bei €. Welche Menge muss von jedem Typ gekauft werden, um die minimalen Kosten zu decken?
1 Auswahl der Unbekannten.
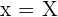
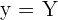
2 Zielfunktion
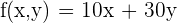
3 Bedingungen
| X | Y | Minimum | |
|---|---|---|---|
| A | 1 | 5 | 15 |
| B | 5 | 1 | 15 |
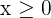
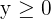
4 Wir bestimmen die Gesamtheit der durchführbaren Lösungen
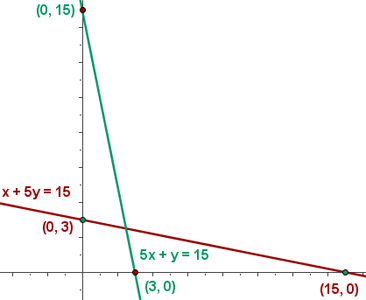
5 Wir berechnen die Koordinaten der Scheitelpunkte des Bereichs der durchführbaren Lösungen.
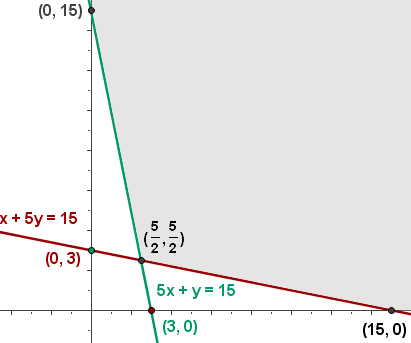
6 Wir berechnen den Wert der Zielfunktion
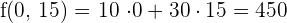
Minimum
Die minimalen Kosten liegen bei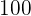 
€ für 
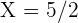und 
.
Berechnen eines Maximalgewinns
Zu Beginn des neuen Schuljahres sollen Schulmaterialien angeboten werden. Ein Kaufhaus möchte 
Hefte, 
Mappen und 
Kugelschreiber anbieten, die auf zwei unterschiedliche Arten verpackt werden. Im ersten Paket sind Hefte, Mappe und Kugelschreiber. Im zweiten Paket sind 
Hefte, Mappe und Kugelschreiber. Die Preise für die Pakete liegen bei jeweils bei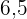 
und 
€. Wie viele Pakete müssen von jeder Art verkauft werden, damit der Maximalgewinn erzielt werden kann?
1 Auswahl der Unbekannten.
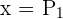
2 Zielfunktion
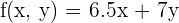
3 Einschränkungen
| P1 | P2 | Verfügbar | |
|---|---|---|---|
| Hefte | 2 | 3 | 600 |
| Mappen | 1 | 1 | 500 |
| Kugelschreiber | 2 | 1 | 400 |
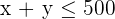
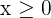
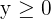
4 Wir bestimmen die Gesamtheit der durchführbaren Lösungen
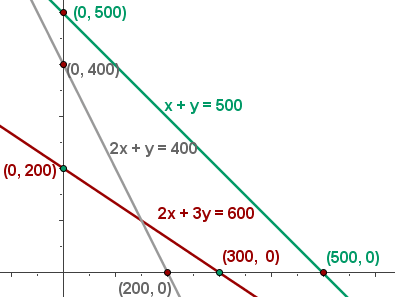
5 Wir berechnen die Koordinaten der Scheitelpunkte des Bereichs der durchführbaren Lösungen.
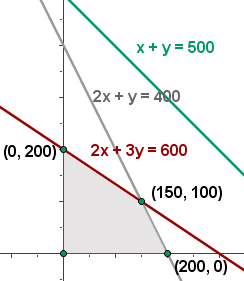
6 Wir berechnen den Wert der Zielfunktion
€
€
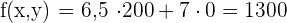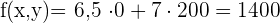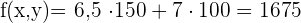€ Maximum
Die optimalen Lösungen sind 150 
und 100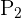 
, damit 
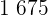€ erzielt werden können.
Berechnen eines Maximalgewinns:
Ein Kaufhaus möchte 
Hemden und Hosen aus der vergangenen Saison abverkaufen. Dazu gibt es zwei Angebote 
und 
. Angebot besteht aus einem Set aus einem Hemd und einer Hose und wird für € angeboten. Angebot besteht aus einem Set aus drei Hemden und einer Hose und wird für € angeboten. Es sollen nicht weniger als Set von Angebot angeboten werden und auch nicht weniger als von Angebot . Wie viele müssen von jedem Set verkauft werden, damit der Maximalgewinn erzielt werden kann?
1 Auswahl der Unbekannten.
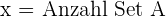
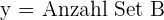
2 Zielfunktion
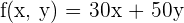
3 Einschränkungen
| A | B | Minimum | |
|---|---|---|---|
| Hemden | 1 | 3 | 200 |
| Hosen | 1 | 1 | 100 |
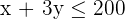
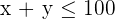
4 Wir bestimmen die Gesamtheit der durchführbaren Lösungen
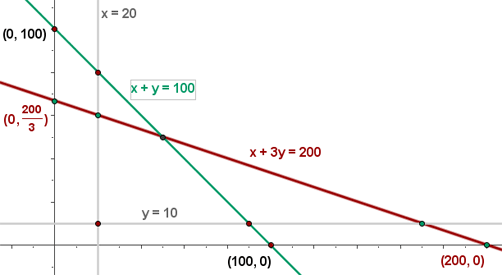
5 Wir berechnen die Koordinaten der Scheitelpunkte des Bereichs der durchführbaren Lösungen.
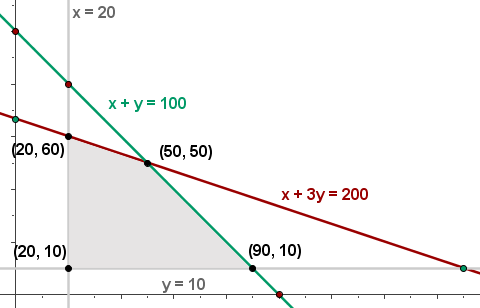
6 Wir berechnen den Wert der Zielfunktion
€
€
€
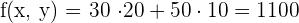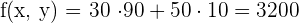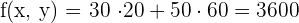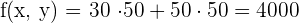€ Maximum
Mit 50 Sets von jedem Typ wird ein Maximalgewinn von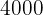 
€ erzielt.
Berechnen eines Maximalgewinns:
Es werden g einer pharmazeutischen Substanz für die Herstellung von großen und kleinen Tabletten benötigt. Die großen Tabletten wiegen g und die kleinen g. Es werden mindestens drei große Tabletten benötigt und mindestens doppelt so viele kleine wie große. Jede große Tablette erzielt einen Gewinn von € und die kleine von €. Wie viele Tabletten müssen jeweils hergestellt werden, damit der Maximalgewinn erzielt werden kann?
1 Auswahl der Unbekannten.
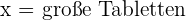
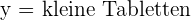
2 Zielfunktion
3 Einschränkungen
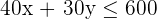
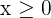
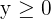
4 Wir bestimmen die Gesamtheit der durchführbaren Lösungen
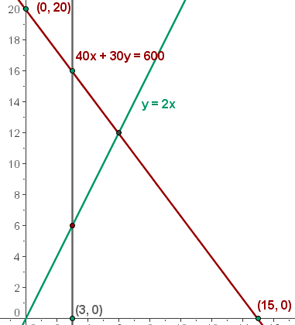
5 span> Wir berechnen die Koordinaten der Scheitelpunkte des Bereichs der durchführbaren Lösungen.
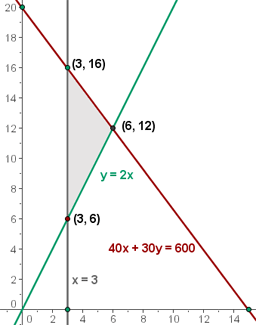
6 Wir berechnen den Wert der Zielfunktion
€
€
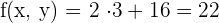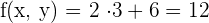€ Maximum
Der Maximalgewinn liegt bei 
€ und wird durch 
große Tabletten und 
kleine Tabletten erzielt.
Berechnen der kostengünstigsten Option
Eine Schule bereitet einen Ausflug für Schüler vor. Das Transportunternehmen hat 
Busse mit Plätzen und mit Plätzen, aber nur 
Fahrer. Die Miete für einen Reisebus beträgt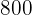 
€, für einen kleinen Bus €. Berechne, wie viele Busse von jedem Typ benötigt werden, damit der Ausflug für die Schule so günstig wie möglich ist.
1 Auswahl der Unbekannten.
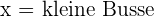
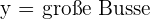
2 Zielfunktion
3 Einschränkungen
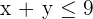
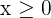
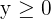
4 Wir bestimmen die Gesamtheit der durchführbaren Lösungen
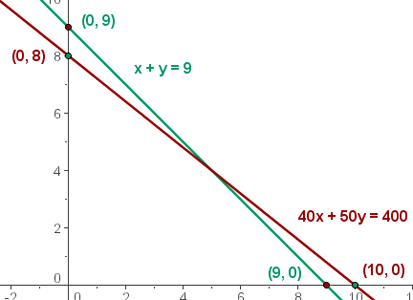
5 Wir berechnen die Koordinaten der Scheitelpunkte des Bereichs der durchführbaren Lösungen.
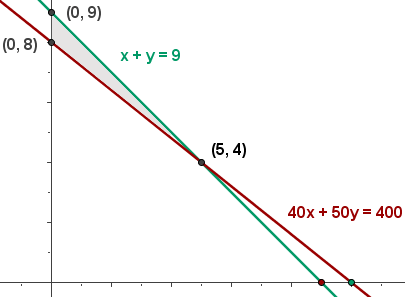
6 Wir berechnen den Wert der Zielfunktion
€
€
€ Minimum
Der Mindestpreis liegt bei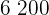 
€, und man benötigt 
große Busse und kleine Busse.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
