1 Die Unbekannten wählen.
2 Die Zielfunktion in Abhängigkeit der Daten des Problems schreiben.
3 Die Einschränkungen in Form eines Ungleichungssystem schreiben.
4 Die Menge der möglichen Lösungen durch grafische Darstellung der Einschränkungen ermitteln.
5 Die Koordinaten der Scheitelpunkte des Bereichs der möglichen Lösungen berechnen (wenn es nur wenige sind).
6 Den Wert der Zielfunktion an jedem der Scheitelpunkte berechnen, um zu sehen, an welchem von ihnen der maximale oder minimale Wert auftritt, je nach Aufgabe (hier muss berücksichtigt werden, dass möglicherweise keine Lösung existiert, wenn der Bereich nicht beschränkt ist).
Beispiel: Für die Herstellung einer Stahlstange des Modells 1 werden 12 Unzen Eisen und 6 Unzen Kohlenstoff benötigt; für die Herstellung einer Stahlstange des Modells 2 werden 8 Unzen Eisen und 20 Unzen Kohlenstoff benötigt. Der Hersteller verfügt über 240 Unzen Eisen und 360 Unzen Kohlenstoff. Der Gewinn pro Barren des Modells 1 beträgt 10 € und pro Barren des Modells 2 15 €. Berechne die optimale Anzahl der zu produzierenden Einheiten der Modelle 1 und 2, um den Gewinn aus dem Verkauf der Stahlstangen zu maximieren..
1 Die Unbekannten wählen.
Anzahl der Barren Modell 1
Anzahl der Barren Modell 2
2 Die Zielfunktion in Abhängigkeit der Daten des Problems schreiben. Dies entspricht dem zu erzielenden Gesamtgewinn.
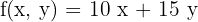
3 Die Einschränkungen in Form eines Ungleichungssystem schreiben.
Wir schreiben die Einschränkungen für das Eisen
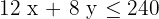
Wir schreiben die Einschränkungen für den Kohlenstoff
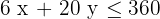
Wir schreiben die Einschränkungen für die Produktion der Barren der Modelle 1 und 2
4 Die Menge der möglichen Lösungen durch grafische Darstellung der Einschränkungen ermitteln.
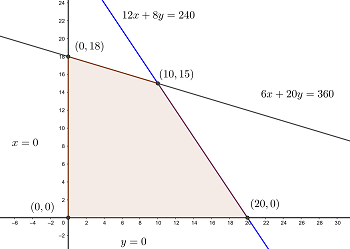
5 Die Koordinaten der Scheitelpunkte des Bereichs der möglichen Lösungen berechnen (wenn es nur wenige sind).
Die Koordinaten sind
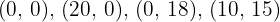
6 Den Wert der Zielfunktion an jedem der Scheitelpunkte berechnen, um zu sehen, an welchem von ihnen der maximale oder minimale Wert auftritt, je nach Aufgabe (hier muss berücksichtigt werden, dass möglicherweise keine Lösung existiert, wenn der Bereich nicht beschränkt ist).
€
€
€
€
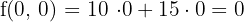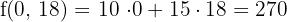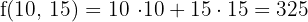Der optimale Wert ist 
. Der maximale Gewinn beträgt somit 325 €, was bei einer Produktion von 10 bzw. 15 Stahlstangen der Modelle 1 und 2 der Fall ist.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
