Die Zahl e begegnet dir vielleicht zum ersten Mal in der Schule – und du fragst dich völlig zu Recht: Was soll dieses komische kleine e eigentlich bedeuten? Ist das eine Variable? Eine Abkürzung? Oder einfach nur Mathe-Magie?
Keine Sorge, wir lüften das Geheimnis! Die sogenannte Eulersche Zahl ist eine der wichtigsten Konstanten der Mathematik – ähnlich wie die Zahl Pi (π). Sie steckt in vielen Formeln, beschreibt Wachstum und Zerfall und taucht sogar in der Wahrscheinlichkeitstheorie und Physik auf.
In diesem Artikel erfährst du, was die Zahl e wirklich ist, wo sie herkommt und warum sie eine so große Rolle spielt.
Die Eulersche Zahl einfach erklärt
Die Eulersche Zahl, auch bekannt als „e“, ist eine mathematische Konstante mit einem ganz besonderen Wert:
e ≈ 2,71828… – eine unendliche, nicht periodische Zahl, ähnlich wie π. Aber was bedeutet das eigentlich?
Einfach gesagt, ist e die Basis der natürlichen Exponentialfunktion, also der Funktion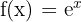 
. Diese Funktion beschreibt viele reale Prozesse – zum Beispiel Wachstum, Zerfall oder das Verhalten in der Wahrscheinlichkeitsrechnung.
Zahlwert und Schreibweise
Da die Zahl e unendlich viele Nachkommastellen hat und sich kein wiederkehrendes Muster erkennen lässt, kann man sie nicht als Bruch oder einfache Dezimalzahl darstellen. Deshalb schreibt man einfach e – kurz, präzise und überall verständlich. Auf deinem Taschenrechner findest du sie meistens unter der Taste 
.
eDie Zahl e ≈ 2,71828... ist eine besondere mathematische Konstante mit diesen Eigenschaften:
🔹 Nicht periodisch:
Die Nachkommastellen von e wiederholen sich nie. Es gibt also kein regelmäßiges Muster wie bei manchen Dezimalzahlen.
🔹 Nicht abbrechend:
e hat unendlich viele Stellen – sie endet also niemals!
🔹 Irrationale Zahl:
Du kannst e nicht als Bruch aus zwei ganzen Zahlen schreiben, ähnlich wie bei der Kreiszahl π.
🔹 Transzendente Zahl:
e ist nicht nur irrational, sondern auch nicht als Lösung einer algebraischen Gleichung mit ganzzahligen Koeffizienten darstellbar. Das unterscheidet sie von Zahlen wie √2, die zwar irrational, aber noch algebraisch sind.
🔹 Mathematische Universalgröße:
e ist die Basis der natürlichen Exponentialfunktion 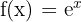und taucht in zahlreichen Bereichen der Mathematik auf – von Logarithmen bis zur Stochastik.
Übrigens: Die Bezeichnung e wurde von Leonhard Euler, einem der bekanntesten Mathematiker überhaupt, eingeführt – daher auch der Name Eulersche Zahl.
Immer noch verwirrt? Dann kann dir vielleicht Mathe Nachhilfe online helfen.
Warum gibt es ein „e“ und keinen ausgeschriebenen Wert?
Die Antwort ist simpel: Weil der exakte Wert von e nicht berechenbar ist – zumindest nicht mit endlichen Mitteln. Deshalb hat sich die Schreibweise mit dem kleinen e durchgesetzt. Sie ist nicht nur praktisch, sondern auch international anerkannt.
Außerdem taucht die Zahl e in unzähligen mathematischen Funktionen auf – vor allem in der Exponentialfunktion, im natürlichen Logarithmus ln(x) und bei der Ableitung bestimmter Funktionen. Deshalb ist es viel einfacher, sie als Symbol zu behandeln als mit einer ellenlangen Dezimalzahl zu arbeiten.
Mach dir keine Sorgen wegen deiner Schwierigkeiten mit der Mathematik. Ich kann dir versichern, dass meine noch größer sind.
Albert Einstein
Wenn du dich fragst, wie e mit der imaginären Zahl i zusammenhängt, lohnt sich ein Blick in unseren Beitrag zur Zahl i.
Die mathematische Definition von e
Die Eulersche Zahl lässt sich nicht nur als Dezimalzahl angeben, sondern auch präzise mathematisch definieren. Tatsächlich gibt es mehrere Wege, um den Wert von e herzuleiten. Die bekanntesten sind die unendliche Reihe und die Grenzwertformel. Beide zeigen, wie tief verwurzelt e in der Mathematik ist.
Die unendliche Reihe nach Euler
Leonhard Euler war der Erste, der e mithilfe einer unendlichen Reihe beschrieben hat. Diese Reihe sieht auf den ersten Blick vielleicht etwas komplex aus, aber das Prinzip ist einfach:
Du summierst immer kleinere Brüche, deren Nenner sogenannte Fakultäten sind.
Formel:
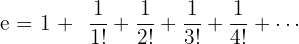
Je mehr Glieder du berechnest, desto genauer wird der Wert von e. Diese Methode ist besonders in der Analysis sehr wichtig.
Die Fakultät ist eine spezielle mathematische Schreibweise, bei der du alle natürlichen Zahlen von 1 bis zu einer bestimmten Zahl miteinander multiplizierst.
Beispiel:
5!=5⋅4⋅3⋅2⋅1=120
Per Definition gilt 0! = 1 – das ist eine mathematische Konvention, die sehr nützlich ist.
Die Grenzwert-Formel
Die zweite wichtige Definition stammt aus der Finanzmathematik – genauer gesagt aus der Zinseszinsrechnung. Je häufiger du Zinsen auf ein Guthaben bekommst, desto schneller wächst es. Wenn du unendlich oft im Jahr Zinsen bekommst, ergibt sich daraus die Eulersche Zahl.
Formel:
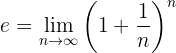
Das heißt: Wenn du 1 Euro mit 100 % Jahreszinsen anlegst und die Zinsen nicht einmal am Ende, sondern kontinuierlich – also in unendlich kleinen Schritten – gutgeschrieben werden, wächst dein Guthaben am Jahresende auf exakt e Euro an.
Eigenschaften der Eulerschen Zahl
Auch wenn die Eulersche Zahl e keine perfekte Zahl ist – hat sie ganz besondere mathematische Eigenschaften, die sie zu einer der faszinierendsten Konstanten überhaupt machen.
Irrational und transzendent – was heißt das?
Zunächst einmal gehört e zu den irrationalen Zahlen. Das bedeutet: Sie kann nicht als Bruch aus zwei ganzen Zahlen dargestellt werden. Ihre Dezimaldarstellung endet nie und zeigt kein regelmäßiges Muster – sie sieht also ähnlich „chaotisch“ aus wie die Zahl π.
Doch es geht noch weiter: e ist sogar eine transzendente Zahl. Das heißt, sie ist nicht die Lösung irgendeiner algebraischen Gleichung mit ganzzahligen Koeffizienten. Nicht einmal ein Polynom wie zum Beispiel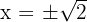 
führt zu e als Ergebnis – selbst die Wurzel aus 2 ist in dem Sinne „einfacher“!
Diese besondere Eigenschaft macht die Eulersche Zahl zu einem echten Exoten unter den bekannten Konstanten – und trotzdem ist sie unglaublich nützlich für Funktionen, Lösungen von Gleichungen oder in der Folge der mathematischen Entwicklung der Analysis.
Du findest Zahlen wie e spannend? Dann schau dir auch mal andere besondere Zahlen der Mathematik an.
Besonderheiten der e-Funktion
Ein echtes Highlight ist die sogenannte natürliche Exponentialfunktion:
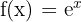
Sie basiert – wie der Name sagt – auf der Eulerschen Zahl und hat eine ganz besondere Eigenschaft: Ihre Ableitung ist identisch mit sich selbst:
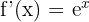
Das bedeutet: Die Steigung dieser Funktion an jeder Stelle ist genauso groß wie ihr Funktionswert. Genau diese Eigenschaft macht sie zu einem unverzichtbaren Werkzeug in der Mathematik, Physik, Biologie oder sogar in der Wirtschaft.
Die e-Funktion spielt auch bei der Umkehrung des natürlichen Logarithmus eine wichtige Rolle. Denn:
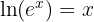und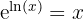 
Online kannst du die e-Funktion ganz einfach selbst ausprobieren – zum Beispiel mit interaktiven Mathe-Webseiten wie GeoGebra oder Desmos. Dort kannst du den Graphen zeichnen, verändern und beobachten, wie er sich verhält. So verstehst du viel besser, warum diese Funktion an jeder Stelle so „besonders“ ist. Auch bei Schulprojekten oder Simulationen im Unterricht ist die e-Funktion super hilfreich – zum Beispiel bei Wachstums- oder Zerfallsprozessen.
Wenn du Hilfe beim Verständnis brauchst, kann dir Mathe Nachhilfe helfen!
Anwendungen der Eulerschen Zahl
Die Eulersche Zahl begegnet dir nicht nur in der Theorie – sie ist fester Bestandteil vieler realer Anwendungen. Ob es um exponentielles Wachstum, Wahrscheinlichkeiten oder Statistik geht: Die Zahl e spielt überall eine Schlüsselrolle. Besonders in den Funktionen, die Prozesse beschreiben, die sich ständig verändern, wie zum Beispiel Bevölkerungswachstum, radioaktiver Zerfall oder das Verteilen von Wahrscheinlichkeiten.
Du wirst sehen: Hinter der scheinbar abstrakten Zahl steckt jede Menge Praxis!
Exponentielles Wachstum und Zerfall
Die natürliche Exponentialfunktion 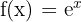wird häufig genutzt, um Wachstumsprozesse oder Zerfallsvorgänge zu beschreiben. Dabei geht es um Situationen, in denen sich etwas kontinuierlich mit einer festen Rate verändert – etwa das Wachstum einer Bakterienkultur, den radioaktiven Zerfall von Stoffen oder auch die Kapitalentwicklung mit Zinseszins. In all diesen Fällen verändert sich die Anzahl oder Menge kontinuierlich über die Zeit hinweg, und genau hier kommt e ins Spiel.
Typisch ist die Gleichung:
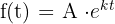
Dabei ist A der Anfangswert, k die Wachstums- oder Zerfallskonstante und t die Zeit.
Während e für stetiges Wachstum steht, symbolisiert die goldene Zahl φ harmonische Proportionen – gemeinsam zeigen sie, wie vielfältig und schön Zahlen die Welt der Mathematik und der Natur durchdringen.
Statistik & Normalverteilung
In der Statistik taucht e in der sogenannten Gaußschen Normalverteilung auf. Diese beschreibt, wie Datenwerte um einen Mittelwert verteilt sind – zum Beispiel Körpergrößen, IQ-Werte oder Messfehler. Die zugehörige Dichtefunktion lautet:
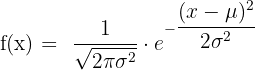
Hierbei stehen μ für den Mittelwert und σ für die Standartabweichung. Die Funktion hilft Unternehmen, Kunden-Verhalten zu analysieren, oder auch Messdaten in der Naturwissenschaft korrekt zu interpretieren.
Von Primzahlen hast Du aber sicher schon einmal etwas gehört, oder?
Wahrscheinlichkeit & Kombinatorik
In der Wahrscheinlichkeitsrechnung begegnet uns e häufig bei sogenannten Grenzwertbetrachtungen. Zum Beispiel bei der Frage:
Wie groß ist die Wahrscheinlichkeit, dass bei n Briefen keiner im richtigen Umschlag landet?
Die Antwort lautet:
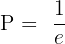
Das sind etwa 36,8 % – ein verblüffendes Ergebnis, das in vielen Modellierungen Anwendung findet. Auch in der Poisson-Verteilung zur Berechnung seltener Ereignisse kommt e ins Spiel.
Die Euler’sche Formel – Verbindung zwischen e, i und φ
Die Euler’sche Formel ist eine der elegantesten und tiefgründigsten Beziehungen in der Mathematik:
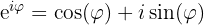
Diese Gleichung verbindet auf geniale Weise drei völlig unterschiedliche Konzepte:
- die Eulersche Zahl e
- die imaginäre Einheit i
- und den Winkel φ dargestellt durch Cosinus und Sinus.
Die Euler’sche Formel zeigt, dass man mit der Exponentialfunktion sogar Drehungen in der komplexen Ebene darstellen kann. Wenn du also eine komplexe Zahl in der Form
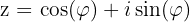
hast, dann kannst du sie viel kompakter auch als
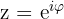
schreiben. Diese Schreibweise nennt man die exponentielle Form einer komplexen Zahl – besonders praktisch in Physik, Elektrotechnik und Ingenieurwesen.
Die Eulersche Identität
Die Eulersche Identität gilt als eine der schönsten Formeln der Mathematik:
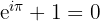
Warum? Weil sie fünf der wichtigsten mathematischen Zahlen verbindet:
- e - die Eulersche Zahl
- i - die imaginäre Zahl
- π
- die 1
- und die 0
Diese Formel ist nicht nur schön, sondern auch nützlich: Sie hilft zum Beispiel, komplexe Zahlen auf eine elegante Weise zu bearbeiten – und macht viele Rechenwege einfacher und kürzer.
Dir gefällt unser Artikel? Hinterlasse eine Bewertung!
Loading...
