Kapitel
- Was ist die Achsenabschnittform der Geradengleichung?
- Allgemeine Geradengleichung
- Die Achsenabschnittsform der Geradengleichung anhand der allgemeinen Form der Geradengleichung
- Zusammenfassung der Vorgehensweise, um die Achsenabschnittsform der Geradengleichung zu erhalten
- Formel der Achsenabschnittsform der Geradengleichung
- Beispiele für Problemstellungen bei der Achsenabschnittsform der Geradengleichung

Was ist die Achsenabschnittform der Geradengleichung?
Die Achsenabschnittsform einer Geradengleichung ist der algebraische Ausdruck einer Geraden, die anhand der Punkte, an denen die Gerade eine der Achsen des Koordinatensystems schneidet, bestimmt werden kann.
Den Wert, an dem die Gerade die  -Achse schneidet, nennen wir
-Achse schneidet, nennen wir  und den Wert, an dem die Gerade die
und den Wert, an dem die Gerade die  -Achse schneidet, nennen wir
-Achse schneidet, nennen wir  , wodurch die zwei Punkte
, wodurch die zwei Punkte  und
und  in der karthesischen Ebene entstehen.
in der karthesischen Ebene entstehen.
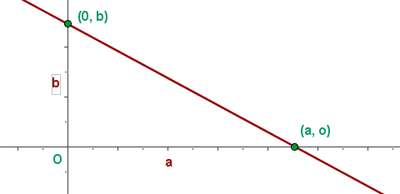
In vielen Fällen haben wir die allgemeine Gleichung der Geraden und davon ausgehend benötigen wir die Achsenabschnittsform der Geradengleichung. Deshalb sehen wir uns die algebraische Vorgehensweise an, damit wir auch den Aufbau der Achsenabschnittsform der Geradengleichung verstehen.
Wir beginnen mit der allgemeinen Geradengleichung.
Allgemeine Geradengleichung

Die Achsenabschnittsform der Geradengleichung anhand der allgemeinen Form der Geradengleichung
Die allgemeine Form der Geradengleichung lautet wie folgt:

Wir gehen davon aus, dass  ist, um die Stelle zu ermitteln, an der die Gerade die
ist, um die Stelle zu ermitteln, an der die Gerade die  -Achse schneidet. Die allgemeine Form der Geradengleichung lautet also:
-Achse schneidet. Die allgemeine Form der Geradengleichung lautet also:
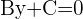
Wir bestimmen  ,
,
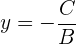
Der ermittelte Wert entspricht 

Mit der gleichen Argumentation können wir den Wert  bestimmen
bestimmen
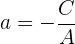
Zusammenfassung der Vorgehensweise, um die Achsenabschnittsform der Geradengleichung zu erhalten
Wenn die allgemeine Form der Geradengleichung wie folgt lautet
 ,
,
gilt
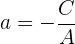

und die Achsenabschnittsform der Geradengleichung ist
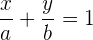
Wenn wir von der allgemeinen Form ausgehen

und das konstante Glied auf die andere Seite bringen
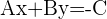
und schließlich durch 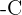 teilen (dieses darf nicht null sein), erhalten wir
teilen (dieses darf nicht null sein), erhalten wir
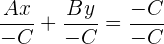
und kommen zu dem Schluss, dass

Die Achsenabschnittsform sieht also wie folgt aus
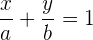
Hierbei gilt:
 ist die Abszisse im Ursprung der Geraden.
ist die Abszisse im Ursprung der Geraden. ist die Ordinate im Ursprung der Geraden.
ist die Ordinate im Ursprung der Geraden.- Das konstante Glied der allgemeinen Gleichung darf NICHT null sein. Dies bedeutet, dass die Achsenabschnittform der Geradengleichung NICHT Geraden beschreibt, die durch den Ursprung verlaufen. Somit gilt
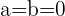
- Wenn
 oder
oder  der allgemeinen Gleichung null sind, bedeutet dies, dass die Gerade jeweils horizontal oder vertikal verläuft. Dies führt dazu, dass
der allgemeinen Gleichung null sind, bedeutet dies, dass die Gerade jeweils horizontal oder vertikal verläuft. Dies führt dazu, dass  oder
oder  der Achsenabschnittsform nicht existieren. Somit gibt es auch für diesen Fall keine Achsenabschnittsform der Geradengleichung.
der Achsenabschnittsform nicht existieren. Somit gibt es auch für diesen Fall keine Achsenabschnittsform der Geradengleichung.
Formel der Achsenabschnittsform der Geradengleichung
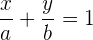
Beispiele für Problemstellungen bei der Achsenabschnittsform der Geradengleichung
1 Eine Gerade legt auf den Koordinatenachsen Segmente zwischen  bzw.
bzw.  Einheiten fest. Bestimme ihre Gleichung.
Einheiten fest. Bestimme ihre Gleichung.
In diesem Fall ist es einfach, da wir anhand der gegebenen Informationen sehen, dass  und
und  . Wir müssen die Werte also nur in die Gleichung einsetzen
. Wir müssen die Werte also nur in die Gleichung einsetzen
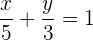
2 Bestimme die Achsenabschnittsform einer Geraden, die durch den Punkt 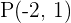 verläuft und den Richtungsvektor
verläuft und den Richtungsvektor  hat.
hat.
Wir stellen fest, dass es aufgrund der uns vorliegenden Informationen sinnvoll ist, die Geradengleichung in ihrer stetigen Form zu verwenden, um ihren Aufbau besser zu verstehen.
Wir haben
- Einen Punkt
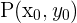 , durch den die Gerade verläuft
, durch den die Gerade verläuft - Einen Richtungsvektor
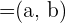 .
.
Die Gleichung der Geraden in ihrer stetigen Form lautet also
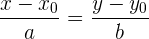 .
.
Damit können wir die Gleichung in ihrer stetigen Form bestimmen:
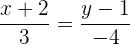 .
.
Mit dieser Gleichung können wir sie nun in die Achsenabschnittsform der Geradengleichung umwandeln.
Aus der allgemeinen Form erhalten wir zunächst die Werte für  und
und  :
:
Wir bringen die Nenner durch Multiplikation auf die andere Seite
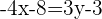
Nun bringen wir alle Ausdrücke auf eine Seite und schreiben die Gleichung in ihrer allgemeinen Form
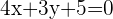
Wir stellen fest, dass  und die Werte
und die Werte  und
und  der allgemeinen Form der Gleichung ungleich null sind.
der allgemeinen Form der Gleichung ungleich null sind.
Wir können also die Achsenabschnittform der Geraden berechnen. Hierbei gilt  und
und 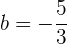 . Wir erhalten
. Wir erhalten

Wir stellen auch fest, dass die Geradengleichung in ihrer Achsenabschnittsform uns die notwendigen Informationen liefert, um andere Berechnungen durchzuführen, z. B. können wir mit der Geraden  , die mit den Achsen ein Dreieck bildet, dessen Flächeninhalt berechnen.
, die mit den Achsen ein Dreieck bildet, dessen Flächeninhalt berechnen.
Die Gerade bildet ein rechtwinkliges Dreieck mit dem Ursprung und ihre Katheten sind die Abszisse und die Ordinate im Ursprung, also die Werte von a und b der Achsenabschnittsform
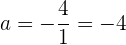

Somit lautet die Achsenabschnittsform der Geradengleichung:
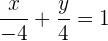
Der Flächeninhalt ist:
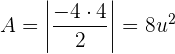
Dieses Ergebnis merken wir uns für unsere nächste Aufgabe.
3 Eine Gerade verläuft durch den Punkt 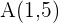 und bildet mit den Koordinatenachsen ein Dreieck mit der Fläche
und bildet mit den Koordinatenachsen ein Dreieck mit der Fläche 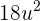 . Wie lautet die Gleichung der Geraden?
. Wie lautet die Gleichung der Geraden?
Wir wenden  und
und 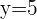 auf die Achsenabschnittsform an:
auf die Achsenabschnittsform an:

Die Fläche des Dreiecks, das die Gerade mit den Achsen bildet, ist:
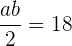
Dadurch entsteht ein Gleichungssystem (zwei Gleichungen, zwei Unbekannte)
Wir lösen das Gleichungssystem:
Wenn wir bei der ersten Gleichung mit 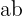 multiplizieren und bei der zweiten Gleichung mit
multiplizieren und bei der zweiten Gleichung mit  , entsteht folgendes System
, entsteht folgendes System
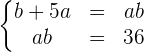
Zur Lösung multiplizieren wir beide Gleichungen mit a
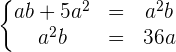
Wir setzen 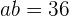 ,
, 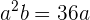 in die Gleichung
in die Gleichung 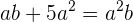 ein und erhalten eine quadratische Gleichung
ein und erhalten eine quadratische Gleichung 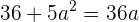 . Wir stellen um und erhalten
. Wir stellen um und erhalten 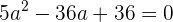 .
.
Wir lösen die quadratische Gleichung und erhalten zwei reelle Lösungen (es gibt zwei Geraden, die die Bedingung erfüllen)
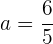 yund
yund 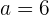
Um dann den Wert für  zu bestimmen, belegen wir die freie Stelle einer Gleichheit. Das heißt,
zu bestimmen, belegen wir die freie Stelle einer Gleichheit. Das heißt, 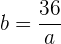
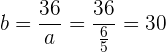 und
und 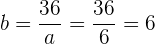
Das bedeutet, dass die beiden Gleichungen der Geraden, die die Bedingung erfüllen, wie folgt lauten:
 und
und 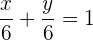
4 Eine Gerade verläuft durch den Punkt  und legt auf den Koordinatenachsen Segmente fest, die auf der x-Achse doppelt so lang sind wie auf der y-Achse. Bestimme die Gleichung dieser Geraden.
und legt auf den Koordinatenachsen Segmente fest, die auf der x-Achse doppelt so lang sind wie auf der y-Achse. Bestimme die Gleichung dieser Geraden.
Die Grafik stellt das Problem anschaulich dar
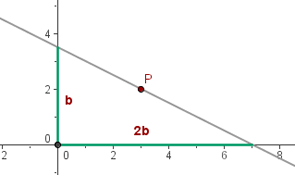
Wir können die Werte in die Achsenabschnittsform der Geradengleichung einsetzen
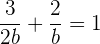
Wir multiplizieren mit  und erhalten
und erhalten
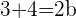
Das bedeutet:
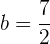
Und somit:
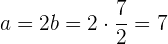
Die gesuchte Gleichung lautet also
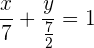
Mit KI zusammenfassen:













