Kapitel

Von der Normalform der Geradengleichung zur allgemeinen Geradengleichung
1 Wir beginnen mit der Normalform der Geradengleichung
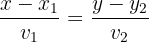
2 Wir lösen die Nenner auf und erhalten:
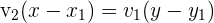
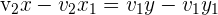
3 Wir bringen die Terme auf die linke Seite:
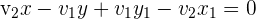
4 Um die Lösung zu vereinfachen, verwenden wir die Buchstaben A, B, und C
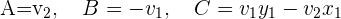
So erhalten wir die allgemeine Geradengleichung:
Die allgemeine Geradengleichung
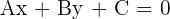
Diese Art von Gleichung wird auch allgemeine oder implizite Geradengleichung genannt.
Die Komponenten des Richtungsvektors

Die Steigung der Geraden
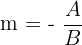
Von der Punkt-Steigungsform der Geraden zur allgemeinen Geradengleichung
Die Form der allgemeinen Geradengleichung zu erhalten ist nicht schwer. Es reicht aus, eine beliebige mathematische Darstellung der Geraden so umzuformen, dass man eine Gleichung gleich Null erhält.
Für den Fall, dass du die allgemeine Geradengleichung auf Basis der Punkt-Steigungs-Form mit Punkt  und Steigung
und Steigung  ermitteln willst, geht man wie folgt vor:
ermitteln willst, geht man wie folgt vor: 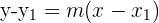 . Folgende Rechenschritte werden benötigt:
. Folgende Rechenschritte werden benötigt:
1 Führe die Multiplikation auf der rechten Seite der Gleichung durch
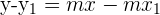
2 Bringe alle Terme auf die linke Seite und setze mit Null gleich
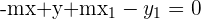
3 Setze A, B und C ein, um die Gleichung zu vereinfachen.
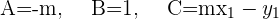
4 Wir erhalten erneut die allgemeine Geradengleichung mit der Form:
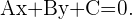
Rechenbeispiele: Geradengleichung
1 Welche Gleichung hat die Gerade, die durch den Punkt 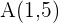 verläuft und deren Richtungsvektor
verläuft und deren Richtungsvektor 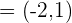 ist?
ist?
Da wir die Koordinaten von 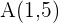 und den Richtungsvektor
und den Richtungsvektor 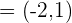 kennen, setzen wir diese Werte in die Normalform der Geradengleichung ein:
kennen, setzen wir diese Werte in die Normalform der Geradengleichung ein:
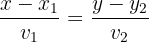
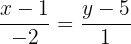
Wir lösen die Nenner auf und erhalten
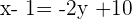
Durch Gleichsetzen mit Null erhalten wir die allgemeine Geradengleichung:
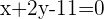
2 Welche Gleichung hat die Gerade, die durch den Punkt  verläuft und die Steigung
verläuft und die Steigung  aufweist?
aufweist?
Da die Koordinaten des Punkts  und die Steigung
und die Steigung  bekannt sind, setzen wir die Werte in die Punkt-Steigungs-Form der Geraden ein:
bekannt sind, setzen wir die Werte in die Punkt-Steigungs-Form der Geraden ein:
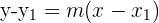
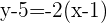
Multipliziere aus:
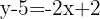
Setze mit Null gleich und du erhältst die allgemeine Geradengleichung:
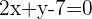
Mit KI zusammenfassen:













