Ermittle die Gleichung der Ebene, die durch den Schnittpunkt der Geraden 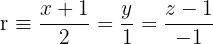 mit der Ebene
mit der Ebene  verläuft und parallel zu folgenden Geraden ist:
verläuft und parallel zu folgenden Geraden ist: 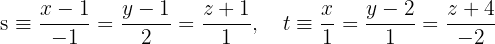
Die stetigen Gleichungen der Geraden r werden in implizite Gleichungen umgewandelt, und diese bilden zusammen mit der Gleichung der Ebene ein System, dessen Lösung der Schnittpunkt ist.
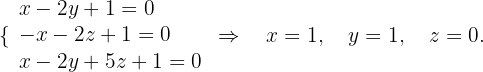
Die Ebene wird durch den Schnittpunkt und die Richtungsvektoren der zur Ebene parallelen Geraden bestimmt.
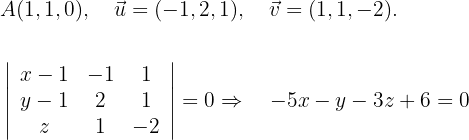
Ermittle die Gleichung einer Geraden, die durch den Punkt 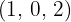 verläuft und an die folgenden Geraden angelehnt ist:
verläuft und an die folgenden Geraden angelehnt ist:
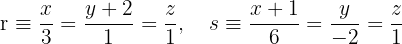 .
.
Wir erhalten einen generischen Punkt auf der Geraden r.
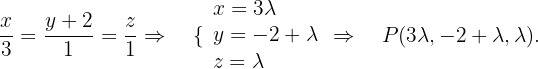
Wir erhalten einen generischen Punkt auf der Geraden s.
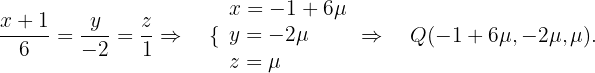
Wir berechnen die Gleichung der Geraden, die durch P und Q verläuft.
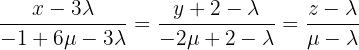
Da die Gerade durch den Punkt 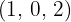 verläuft, erhalten wir:
verläuft, erhalten wir:
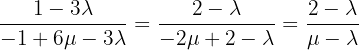
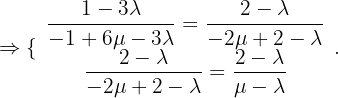
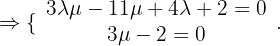
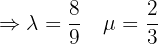
Wir setzen diese beiden Werte in die Gleichung der Geraden ein:
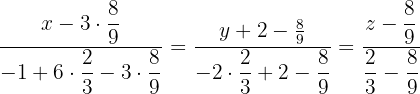
Wir führen die entsprechenden Berechnungen durch und vereinfachen.
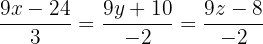
Ermittle die Werte der Parameter a und b, so dass die Gerade 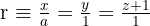 mit der Ebene
mit der Ebene  übereinstimmt.
übereinstimmt.
Die stetigen Gleichungen der Geraden r werden in implizite Gleichungen umgewandelt, und diese bilden zusammen mit der Gleichung der Ebene das folgende System:
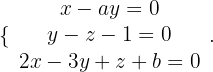
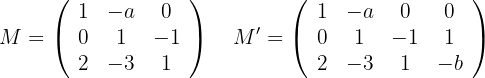
Damit die Gerade mit der Ebene übereinstimmt, muss gelten:
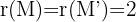
Daher hebt sich die Determinante der Ordnung 3 der beiden Matrizen auf.
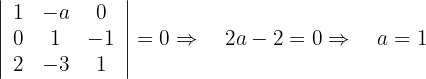
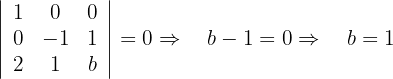
Berechne die Werte der Parameter  und
und  , so dass die Ebenen:
, so dass die Ebenen:
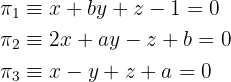
auf derselben Geraden verlaufen.
Damit die drei Ebenen durch dieselbe Gerade verlaufen, muss dies der Fall sein:
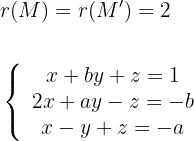
Und somit
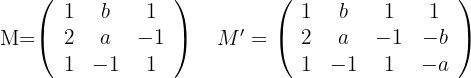
Wir berechnen also  :
:
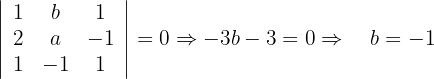
Schließlich berechnen wir  :
:
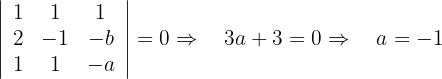
Untersuche die relative Lage der folgenden Ebenen für verschiedene Werte von a:
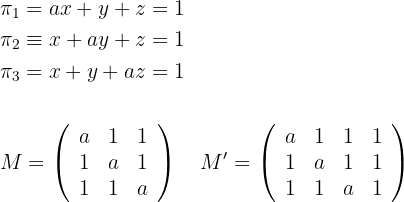
Bei der Determinante der Koeffizientenmatrix addieren wir die beiden anderen Zeilen zur ersten Zeile und klammern dann den gemeinsamen Faktor aus.
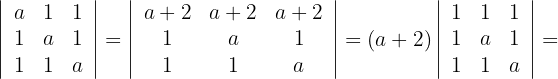
Wir subtrahieren die erste Zeile von jeder Zeile:
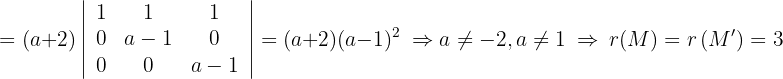
Daher schneiden sich die drei Ebenen in einem Punkt.
Auch wenn 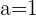 . Die drei Gleichungen sind identisch, so dass die drei Ebenen zusammenfallen.
. Die drei Gleichungen sind identisch, so dass die drei Ebenen zusammenfallen.
Aber wenn 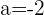 ,
,
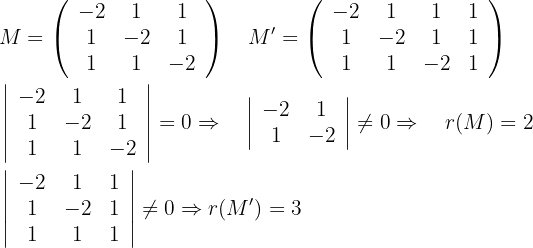
Da es kein Paar paralleler Ebenen gibt, schneiden sich die drei Ebenen paarweise und bilden eine prismatische Fläche.
Untersuche die relativen Lagen der Ebene 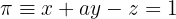 und der Geraden
und der Geraden 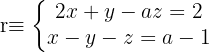
anhand der Werte des Parameters  .
.
Wir bilden das folgende Gleichungssystem:
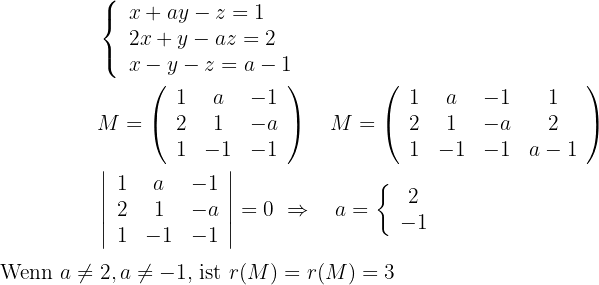
Die Gerade schneidet die Ebene an einem einzigen Punkt.
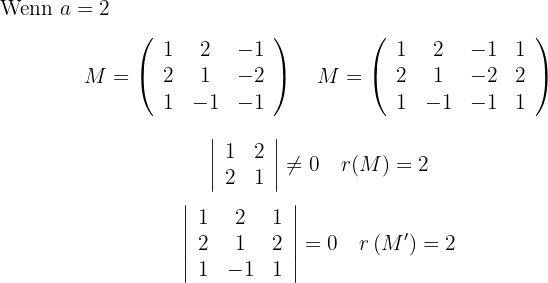
Die Gerade ist in der Ebene enthalten.
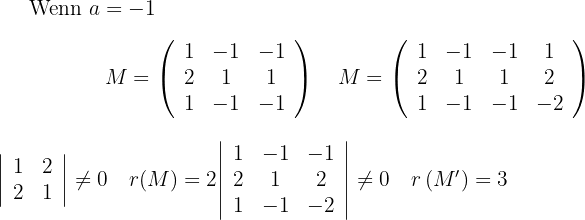
Die Gerade ist parallel zur Ebene.
Bestimme  , so dass die Gerade
, so dass die Gerade 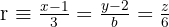 die Ebene
die Ebene 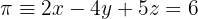 nicht schneidet.
nicht schneidet.
Erinnern wir uns zunächst daran, dass eine Gerade und eine Ebene sich nicht schneiden, wenn sie parallel sind. Damit eine Gerade und eine Ebene parallel sind, ist das Skalarprodukt aus dem Vektor der Gerade und dem Normalenvektor der Ebene gleich 0. 
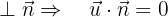
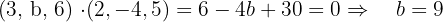
Ermittle die Werte von  und
und  , so dass die Geraden
, so dass die Geraden 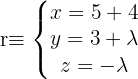 und
und 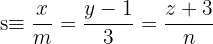 .
.
Wenn zwei Geraden parallel sind, müssen ihre Richtungsvektoren proportional sein.: 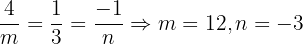 .
.
Berechne den Wert von k, so dass die Geraden 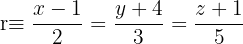 und
und  sich in einem Punkt schneiden. Ermittle diesen Punkt.
sich in einem Punkt schneiden. Ermittle diesen Punkt.
Zunächst können wir die Gleichung der Geraden r als Schnittpunkt zweier Ebenen umschreiben:
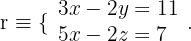
Wir können dann eine der Definitionsgleichungen der Geraden  heranziehen, um ein System von drei Gleichungen mit drei Unbekannten zu konstruieren und den Schnittpunkt der drei Ebenen zu berechnen, d. h:
heranziehen, um ein System von drei Gleichungen mit drei Unbekannten zu konstruieren und den Schnittpunkt der drei Ebenen zu berechnen, d. h:
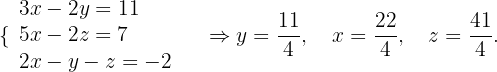
Da der erhaltene Punkt die vier Gleichungen der Ebenen erfüllen muss, können wir die Werte von 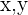 und
und  in die Gleichung
in die Gleichung 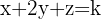 einsetzen, um
einsetzen, um  zu bestimmen:
zu bestimmen: 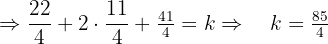
Mit KI zusammenfassen:


