Ermittle die Gleichung der Geraden, die durch die Punkte 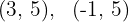 verläuft und gib an, ob sie parallel zu den Koordinatenachsen ist.
verläuft und gib an, ob sie parallel zu den Koordinatenachsen ist.
1 Wir berechnen die Steigung der Geraden durch den Quotienten aus der Differenz der zweiten Koordinaten und der Differenz der ersten Koordinaten der Punkte

Da die Steigung 0 ist, entspricht die Gerade der  -Achse oder ist parallel dazu.
-Achse oder ist parallel dazu.
2 Damit die Gerade auf der  -Achse liegt, müssen alle Punkte auf der Geraden eine zweite Koordinate haben, die gleich 0 ist. Da die Gerade durch den Punkt
-Achse liegt, müssen alle Punkte auf der Geraden eine zweite Koordinate haben, die gleich 0 ist. Da die Gerade durch den Punkt  verläuft, dessen zweite Koordinate ungleich 0 ist, ergibt sich, dass die Gerade parallel zur
verläuft, dessen zweite Koordinate ungleich 0 ist, ergibt sich, dass die Gerade parallel zur  -Achse verläuft.
-Achse verläuft.
3 Die Gleichung einer zur  -Achse parallelen Geraden hat die Form
-Achse parallelen Geraden hat die Form
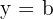 ,
,
wobei  der 2. Koordinate eines beliebigen Punktes auf der horizontalen Geraden entspricht. Somit lautet die Gleichung der Geraden
der 2. Koordinate eines beliebigen Punktes auf der horizontalen Geraden entspricht. Somit lautet die Gleichung der Geraden

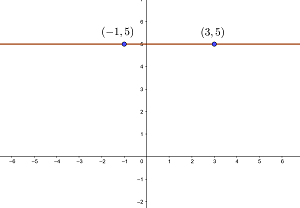
Ermittle die Gleichung der Geraden, die durch die Punkte 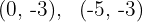 verläuft und gib an, ob sie parallel zu den Koordinatenachsen ist.
verläuft und gib an, ob sie parallel zu den Koordinatenachsen ist.
1 Wir berechnen die Steigung der Geraden durch den Quotienten aus der Differenz der zweiten Koordinaten und der Differenz der ersten Koordinaten der Punkte
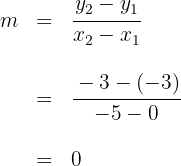
Da die Steigung 0 ist, entspricht die Gerade der  -Achse oder ist parallel dazu.
-Achse oder ist parallel dazu.
2 Damit die Gerade auf der  -Achse liegt, müssen alle Punkte auf der Geraden eine zweite Koordinate haben, die gleich 0 ist. Da die Gerade durch den Punkt
-Achse liegt, müssen alle Punkte auf der Geraden eine zweite Koordinate haben, die gleich 0 ist. Da die Gerade durch den Punkt  verläuft, dessen zweite Koordinate ungleich 0 ist, kann man daraus schließen, dass die Gerade parallel zur
verläuft, dessen zweite Koordinate ungleich 0 ist, kann man daraus schließen, dass die Gerade parallel zur  -Achse verläuft
-Achse verläuft
3 Die Gleichung einer zur  -Achse parallelen Geraden hat die Form
-Achse parallelen Geraden hat die Form
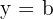 ,
,
wobei  der 2. Koordinate eines beliebigen Punktes auf der horizontalen Geraden entspricht. Somit lautet die Gleichung der Geraden
der 2. Koordinate eines beliebigen Punktes auf der horizontalen Geraden entspricht. Somit lautet die Gleichung der Geraden

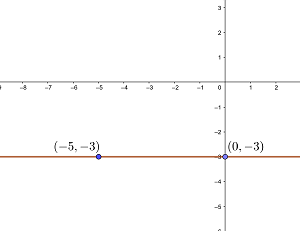
Ermittle die Gleichung der Geraden, die senkrecht zur  -Achse und durch den Punkt
-Achse und durch den Punkt  verläuft, und gib an, ob sie parallel zu den Koordinatenachsen ist.
verläuft, und gib an, ob sie parallel zu den Koordinatenachsen ist.
1 Da die  -Achse eine senkrechte Gerade ist, ist die gesuchte Senkrechte eine waagerechte Gerade. Ihre Steigung ist also 0
-Achse eine senkrechte Gerade ist, ist die gesuchte Senkrechte eine waagerechte Gerade. Ihre Steigung ist also 0
Da die Steigung gleich 0 ist, ist die Gerade die  -Koordinatenachse oder verläuft parallel zu ihr.
-Koordinatenachse oder verläuft parallel zu ihr.
2 Damit die Gerade auf der 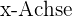 liegt, müssen alle Punkte auf der Geraden eine zweite Koordinate haben, die gleich 0 ist. Da die Gerade durch den Punkt
liegt, müssen alle Punkte auf der Geraden eine zweite Koordinate haben, die gleich 0 ist. Da die Gerade durch den Punkt  verläuft, dessen zweite Koordinate ungleich 0 ist, ergibt sich, dass die Gerade parallel zur
verläuft, dessen zweite Koordinate ungleich 0 ist, ergibt sich, dass die Gerade parallel zur  -Achse verläuft
-Achse verläuft
3 Die Gleichung einer zur  -Achse parallelen Geraden hat die Form
-Achse parallelen Geraden hat die Form
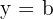 ,
,
wobei  der 2. Koordinate eines beliebigen Punktes auf der horizontalen Geraden entspricht. Somit lautet die Gleichung der Geraden
der 2. Koordinate eines beliebigen Punktes auf der horizontalen Geraden entspricht. Somit lautet die Gleichung der Geraden

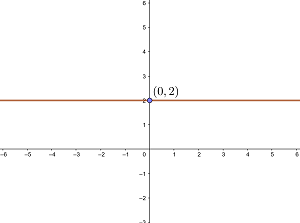
Ermittle die Gleichung der Geraden mit der Steigung 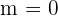 , die durch den Punkt
, die durch den Punkt 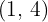 verläuft, und gib an, ob sie parallel zu den Koordinatenachsen ist.
verläuft, und gib an, ob sie parallel zu den Koordinatenachsen ist.
1 Da die Steigung gleich 0 ist, ist die Gerade die  -Koordinatenachse oder verläuft parallel zu ihr.
-Koordinatenachse oder verläuft parallel zu ihr.
2 Damit die Gerade auf der 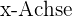 liegt, müssen alle Punkte auf der Geraden eine zweite Koordinate haben, die gleich 0 ist. Da die Gerade durch den Punkt
liegt, müssen alle Punkte auf der Geraden eine zweite Koordinate haben, die gleich 0 ist. Da die Gerade durch den Punkt 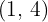 verläuft, dessen zweite Koordinate ungleich 0 ist, ergibt sich, dass die Gerade parallel zur
verläuft, dessen zweite Koordinate ungleich 0 ist, ergibt sich, dass die Gerade parallel zur  -Achse verläuft
-Achse verläuft
3 Die Gleichung einer zur  -Achse parallelen Geraden hat die Form
-Achse parallelen Geraden hat die Form
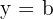 ,
,
wobei  der 2. Koordinate eines beliebigen Punktes auf der horizontalen Geraden entspricht. Somit lautet die Gleichung der Geraden
der 2. Koordinate eines beliebigen Punktes auf der horizontalen Geraden entspricht. Somit lautet die Gleichung der Geraden

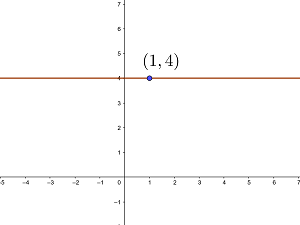
Ermittle die Gleichung der Geraden, die durch die Punkte 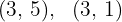 verläuft, und gib an, ob sie parallel zu den Koordinatenachsen ist.
verläuft, und gib an, ob sie parallel zu den Koordinatenachsen ist.
1 Wir berechnen die Steigung der Geraden durch den Quotienten aus der Differenz der zweiten Koordinaten und der Differenz der ersten Koordinaten der Punkte
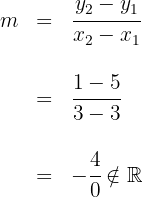
Da die Steigung nicht zu den reellen Zahlen gehört, ist die Gerade die Koordinatenachse  oder verläuft parallel zu ihr.
oder verläuft parallel zu ihr.
2 Damit die Gerade auf der  -Achse liegt, müssen alle Punkte auf der Geraden eine erste Koordinate gleich 0 haben. Da die Gerade durch den Punkt
-Achse liegt, müssen alle Punkte auf der Geraden eine erste Koordinate gleich 0 haben. Da die Gerade durch den Punkt  verläuft, dessen erste Koordinate ungleich 0 ist, kann man daraus schließen, dass die Gerade parallel zur
verläuft, dessen erste Koordinate ungleich 0 ist, kann man daraus schließen, dass die Gerade parallel zur  -Achse verläuft
-Achse verläuft
3 Die Gleichung einer zur  -Achse parallelen Geraden hat die Form
-Achse parallelen Geraden hat die Form
 ,
,
wobei  der ersten Koordinate eines beliebigen Punktes auf der vertikalen Geraden entspricht. Die Gleichung der Geraden lautet also
der ersten Koordinate eines beliebigen Punktes auf der vertikalen Geraden entspricht. Die Gleichung der Geraden lautet also

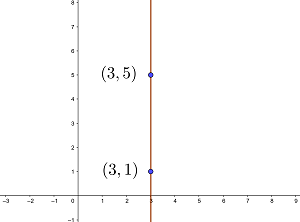
Bestimme die Gleichung der Geraden, die durch die Punkte  verläuft, und gib an, ob sie parallel zu den Koordinatenachsen ist.
verläuft, und gib an, ob sie parallel zu den Koordinatenachsen ist.
1 Wir berechnen die Steigung der Geraden durch den Quotienten aus der Differenz der zweiten Koordinaten und der Differenz der ersten Koordinaten der Punkte

Da die Steigung nicht zu den reellen Zahlen gehört, ist die Gerade die  -Achse oder verläuft parallel zu ihr.
-Achse oder verläuft parallel zu ihr.
2 Damit die Gerade auf der  -Achse liegt, müssen alle Punkte auf der Geraden eine erste Koordinate gleich 0 haben. Da die Gerade durch den Punkt
-Achse liegt, müssen alle Punkte auf der Geraden eine erste Koordinate gleich 0 haben. Da die Gerade durch den Punkt 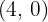 verläuft, dessen erste Koordinate ungleich 0 ist, ergibt sich, dass die Gerade parallel zur
verläuft, dessen erste Koordinate ungleich 0 ist, ergibt sich, dass die Gerade parallel zur  -Achse verläuft.
-Achse verläuft.
3 Die Gleichung einer zur  -Achse parallelen Geraden hat die Form
-Achse parallelen Geraden hat die Form
 ,
,
wobei  der ersten Koordinate eines beliebigen Punktes auf der vertikalen Geraden entspricht. Die Gleichung der Geraden lautet also
der ersten Koordinate eines beliebigen Punktes auf der vertikalen Geraden entspricht. Die Gleichung der Geraden lautet also

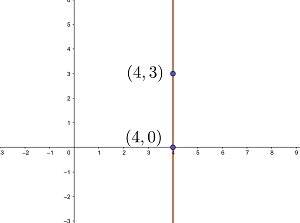
Ermittle die Gleichung der Geraden, die senkrecht zur  -Achse und durch den Punkt
-Achse und durch den Punkt  verläuft, und gib an, ob sie parallel zu den Koordinatenachsen ist.
verläuft, und gib an, ob sie parallel zu den Koordinatenachsen ist.
1 Da die  -Achse eine horizontale Gerade ist, handelt es sich bei der gesuchten Senkrechten um eine Vertikale, deren Steigung gegen unendlich geht, so dass sie nicht zu den reellen Zahlen gehört.
-Achse eine horizontale Gerade ist, handelt es sich bei der gesuchten Senkrechten um eine Vertikale, deren Steigung gegen unendlich geht, so dass sie nicht zu den reellen Zahlen gehört.
Da die Steigung nicht zu den reellen Zahlen gehört, ist die Gerade die  -Koordinatenachse oder verläuft parallel zu ihr
-Koordinatenachse oder verläuft parallel zu ihr
2 Damit die Gerade auf der  -Achse liegt, müssen alle Punkte auf der Geraden eine erste Koordinate gleich 0 haben. Da die Gerade durch den Punkt
-Achse liegt, müssen alle Punkte auf der Geraden eine erste Koordinate gleich 0 haben. Da die Gerade durch den Punkt  verläuft, dessen erste Koordinate ungleich 0 ist, kann man daraus schließen, dass die Gerade parallel zur
verläuft, dessen erste Koordinate ungleich 0 ist, kann man daraus schließen, dass die Gerade parallel zur  -Achse verläuft
-Achse verläuft
3 Die Gleichung einer zur  -Achse parallelen Geraden hat die Form
-Achse parallelen Geraden hat die Form
 ,
,
dwobei  der ersten Koordinate eines beliebigen Punktes auf der vertikalen Geraden entspricht. Die Gleichung der Geraden lautet also
der ersten Koordinate eines beliebigen Punktes auf der vertikalen Geraden entspricht. Die Gleichung der Geraden lautet also

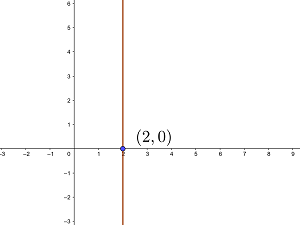
Ermittle die Gleichung der Geraden, die senkrecht zu  steht und durch den Punkt
steht und durch den Punkt 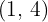 verläuft.
verläuft.
1 Da die Gerade senkrecht auf der vertikalen Geraden  steht, ist die gesuchte Gerade die
steht, ist die gesuchte Gerade die  -Achse oder verläuft parallel zu ihr
-Achse oder verläuft parallel zu ihr
2 Damit die Gerade auf der  -Achse liegt, müssen alle Punkte auf der Geraden eine erste Koordinate gleich 0 haben. Da die Gerade durch den Punkt
-Achse liegt, müssen alle Punkte auf der Geraden eine erste Koordinate gleich 0 haben. Da die Gerade durch den Punkt 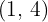 verläuft, dessen erste Koordinate ungleich 0 ist, ergibt sich, dass die Gerade parallel zur
verläuft, dessen erste Koordinate ungleich 0 ist, ergibt sich, dass die Gerade parallel zur  -Achse verläuft.
-Achse verläuft.
3 Die Gleichung einer zur  -Achse parallelen Geraden hat die Form
-Achse parallelen Geraden hat die Form
 ,
,
wobei  der ersten Koordinate eines beliebigen Punktes auf der vertikalen Geraden entspricht. Die Gleichung der Geraden lautet also
der ersten Koordinate eines beliebigen Punktes auf der vertikalen Geraden entspricht. Die Gleichung der Geraden lautet also

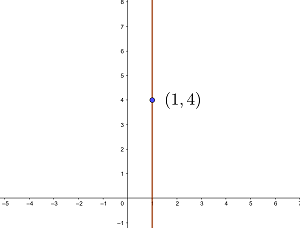
Ermittle die Gleichung der Geraden, die senkrecht zur  -Achse verläuft und durch den Punkt
-Achse verläuft und durch den Punkt  geht.
geht.
1 Da die  -Achse eine senkrechte Gerade ist, ist die gesuchte senkrechte Gerade eine waagerechte Gerade, ihre Steigung ist also 0.
-Achse eine senkrechte Gerade ist, ist die gesuchte senkrechte Gerade eine waagerechte Gerade, ihre Steigung ist also 0.
Da die Steigung gleich 0 ist, ist die Gerade die  -Achse oder verläuft parallel zu ihr.
-Achse oder verläuft parallel zu ihr.
2 Damit die Gerade auf der  -Achse liegt, müssen alle Punkte auf der Geraden eine zweite Koordinate haben, die gleich 0 ist. Da die Gerade durch den Punkt
-Achse liegt, müssen alle Punkte auf der Geraden eine zweite Koordinate haben, die gleich 0 ist. Da die Gerade durch den Punkt  verläuft, dessen zweite Koordinate gleich 0 ist, ergibt sich, dass die Gerade mit der
verläuft, dessen zweite Koordinate gleich 0 ist, ergibt sich, dass die Gerade mit der  -Achse übereinstimmt
-Achse übereinstimmt
3 Die Gleichung einer Geraden, die mit der Achse  übereinstimmt, hat die Form
übereinstimmt, hat die Form

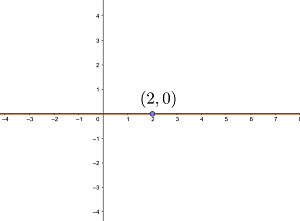
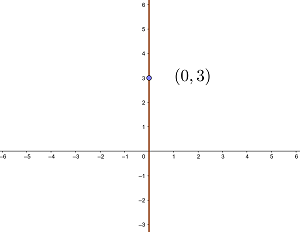
Ermittle die Gleichung der Geraden, die senkrecht zur  -Achse verläuft und durch den Punkt
-Achse verläuft und durch den Punkt  geht.
geht.
1 Da die  -Achse eine horizontale Gerade ist, handelt es sich bei der gesuchten Senkrechten um eine Vertikale, deren Steigung gegen unendlich geht, so dass sie nicht zu den reellen Zahlen gehört.
-Achse eine horizontale Gerade ist, handelt es sich bei der gesuchten Senkrechten um eine Vertikale, deren Steigung gegen unendlich geht, so dass sie nicht zu den reellen Zahlen gehört.
Da die Steigung nicht zu den reellen Zahlen gehört, ist die Gerade die  -Achse oder verläuft parallel zu ihr.
-Achse oder verläuft parallel zu ihr.
2 Damit die Gerade auf der  -Achse liegt, müssen alle Punkte auf der Geraden eine erste Koordinate gleich 0 haben. Da die Gerade durch den Punkt
-Achse liegt, müssen alle Punkte auf der Geraden eine erste Koordinate gleich 0 haben. Da die Gerade durch den Punkt  verläuft, dessen erste Koordinate gleich 0 ist, kann man daraus schließen, dass die Gerade die
verläuft, dessen erste Koordinate gleich 0 ist, kann man daraus schließen, dass die Gerade die  -Achse ist
-Achse ist
3 Die Gleichung einer Geraden, die mit der Achse  übereinstimmt, hat die Form
übereinstimmt, hat die Form

Mit KI zusammenfassen:


