
Die Ebenengleichung bestimmen
Gegeben sind die Geraden:

Bestimme die Gleichung der Ebene, die  enthält und parallel zu
enthält und parallel zu  ist.
ist.
Wir denken daran, dass eine Ebene durch 1 Punkt und 2 Vektoren definiert ist.
Wir lösen 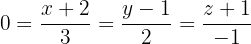 und erhalten A=(-2,1,-1), der ein Punkt auf
und erhalten A=(-2,1,-1), der ein Punkt auf  und somit ein Punkt auf der Ebene ist.
und somit ein Punkt auf der Ebene ist.
Ein Punkt auf der Ebene ist: 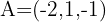
Die Richtungsvektoren sind: 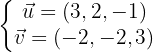
Schließlich ist die Ebenengleichung durch die folgende Determinante gegeben
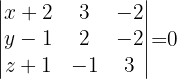
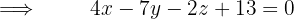
Bestimme die Gleichung der Ebene, die folgende Geraden enthält:

Wir denken daran, dass eine Ebene durch 1 Punkt und 2 Vektoren definiert ist. Wir lösen  und erhalten A=(-2,1,-3), der ein Punkt auf
und erhalten A=(-2,1,-3), der ein Punkt auf  und somit ein Punkt auf der Ebene ist.Ein Punkt auf der Ebene ist:
und somit ein Punkt auf der Ebene ist.Ein Punkt auf der Ebene ist: 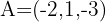
Die Vektoren sind: 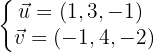
Die Ebenengleichung ist daher durch die folgende Determinante gegeben

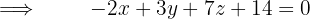
Bestimme die Gleichung der Ebene, die den Punkt A (2, 5, 1) sowie die Gerade der folgenden Gleichung enthält:
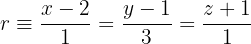
Aus der Parametrierung erhalten wir einen Richtungsvektor 
Wir lösen 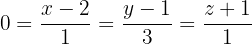 und wissen, dass B (2,1,-1) ein Punkt auf
und wissen, dass B (2,1,-1) ein Punkt auf  ist.
ist.
Somit ist der andere ermittelte Vektor gegeben durch
Ein Punkt auf der Ebene ist: A (2, 5, 1)
Die Richtungsvektoren sind: 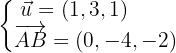
Die Ebenengleichung ist daher durch folgende Determinante gegeben
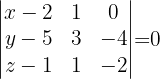
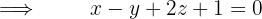
Bestimme die Gleichung der Ebene, die die Gerade  enthält und parallel zur Geraden ist
enthält und parallel zur Geraden ist
Aus der parameterfreien Form der Gleichung der in der Ebene enthaltenen Geraden und der Gleichung der parallelen Geraden in Parameterform ergeben sich 2 Richtungsvektoren der Ebene.Ein Punkt auf der Ebene ist: A (2, 2, 4)
Die Richtungsvektoren sind: 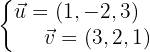
Die Gleichung der Ebene ist daher durch folgende Determinante gegeben
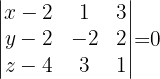
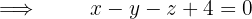
Verschiedene Problemstellungen der Ebenengleichung
Bestimme die Gleichung der Ebene, die durch die Punkte A (1, −2, 4), B (0, 3, 2) verläuft und parallel zu der Geraden 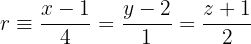 ist.
ist.
Ein Richtungsvektor dieser Ebene wird ein Richtungsvektor der Geraden  sein
sein
Der andere Vektor ist gegeben durch
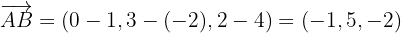
Ein Punkt auf der Ebene ist: A(1, −2, 4)
Die Richtungsvektoren sind: 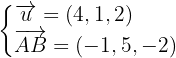
Die Ebenengleichung ist daher durch folgende Determinante gegeben

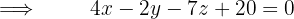
Gegeben ist eine Ebene π, die durch den Punkt P (1, 2, 1) verläuft und die positiven Halbachsen an den Punkten A, B und C schneidet. Das Dreieck ABC ist hierbei gleichseitig. Bestimme die Gleichungen von π.
Wir kennen die Punkte, an denen die Ebene die Achsen schneidet
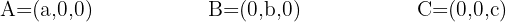
Die Gleichung der Ebene in Achsenabschnittsform ist gegeben durch

Da das Dreieck gleichseitig ist, sind die drei Abschnitte der positiven Halbachsen vom Ursprung bis zum Schnittpunkt gleich. Somit lautet die Gleichung:

Um den Wert für  zu ermitteln, genügt es, die Koordinaten des Punktes P (1, 2, 1) in die Gleichung einzusetzen
zu ermitteln, genügt es, die Koordinaten des Punktes P (1, 2, 1) in die Gleichung einzusetzen

Die Ebenengleichung lautet somit
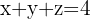
Bestimme die Gleichungen der Koordinatenachsen und der Koordinatenebenen.
1 Achse OX Punkt auf der Geraden: O(0,0,0) Richtungsvektor: 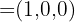 Gleichung in Achsenabschnittsform:
Gleichung in Achsenabschnittsform:  Implizite Darstellung:
Implizite Darstellung: 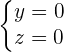
2 Achse OY Punkt auf der Geraden: O(0,0,0) Richtungsvektor: 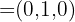 Gleichung in Achsenabschnittsform:
Gleichung in Achsenabschnittsform:  Implizite Darstellung:
Implizite Darstellung: 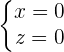
3 Achse OZ Punkt auf der Geraden: O(0,0,0) Richtungsvektor: 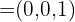 Gleichung in Achsenabschnittsform:
Gleichung in Achsenabschnittsform: 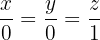 Implizite Darstellung:
Implizite Darstellung: 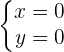
4 Ebene XY
Punkt auf der Ebene: O(0,0,0) Richtungsvektoren: 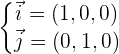 Die Ebenengleichung ist daher durch folgende Determinante gegeben
Die Ebenengleichung ist daher durch folgende Determinante gegeben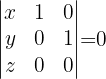

5 Ebene XZ
Punkt auf der Ebene: O(0,0,0)
Richtungsvektoren: 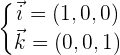
Die Ebenengleichung ist daher durch folgende Determinante gegeben


6 Ebene YZ
Punkt auf der Ebene: O(0,0,0)
Richtungsvektoren: 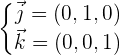
Die Ebenengleichung ist daher durch folgende Determinante gegeben


Bestimme den gemeinsamen Punkt der Ebene 
und der Geraden, die durch den Punkt (1, −3, 2) und den Vektor  definiert ist
definiert ist
1 Wir ermitteln die Gleichung der beschriebenen Geraden
Mit dem Richtungsvektor und dem Punkt, der auf der Geraden liegt, können wir die Gleichung in Parameterform aufstellen
2 Wir setzen in die Ebenengleichung ein
Wir möchten den Punkt finden, der auf der Geraden und auf der Ebene liegt, also müssen die Koordinaten die Gleichungen erfüllen, die sie definieren. Wir nutzen die Koordinaten in Parameterform und setzen sie in die Ebenengleichung ein

Wir lösen die Klammern auf

Wir vereinfachen und bestimmen 

3 Wir berechnen die Koordinaten mit dem Wert 
Die Koordinaten des gemeinsamen Punktes sind (3,1,3)
Bestimme die implizite Gleichung der Ebene, die durch den Punkt P(1, 1, 1) verläuft und parallel ist zu:
Aus der Gleichung in Parameterform der Ebene, zu der sie parallel ist, erhalten wir zwei Richtungsvektoren
Richtungsvektoren: 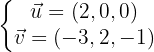
Ein Punkt auf der Ebene: P(1,1,1)
Die Ebenengleichung ist daher durch folgende Determinante gegeben
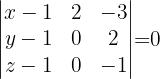
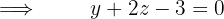
Bestimme die Gleichung der Ebene, die parallel zu folgenden Geradengleichungen ist

und durch den Punkt (1, 1, 2) verläuft.
1 Ermittle die Gleichung von  in Parameterform
in Parameterform
Wir möchten von jeder der parallelen Geraden einen Richtungsvektor erhalten. Aus der impliziten Gleichung von  geht diese Information allerdings nicht direkt hervor. Hierfür müssen wir wir die Gleichung in Parameterform ermitteln.
geht diese Information allerdings nicht direkt hervor. Hierfür müssen wir wir die Gleichung in Parameterform ermitteln.
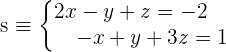
1. Wir bringen eine der Variablen auf die andere Seite der Gleichung.
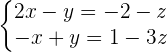
2. Wir wenden die Cramersche Regel an, um x und y in Bezug auf z zu lösen
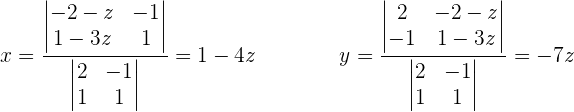
3. Wir erhalten 2 Punkte auf der Geraden, indem wir z zwei Werte zuweisen


4. Wir ermitteln einen Richtungsvektor
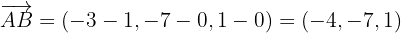
und somit den Punkt A auf s
2 Wir erhalten die Ebenengleichung
Ein Punkt auf der Ebene ist: A (1, 1, 2)
Die Richtungsvektoren sind: 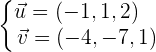
Die Ebenengleichung ist daher durch folgende Determinante gegeben
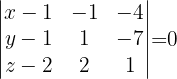
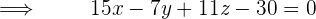
Mit KI zusammenfassen:













