Die Koordinaten der aufeinanderfolgenden Eckpunkte eines Parallelogramms sind 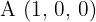 und
und 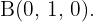 Die Koordinaten des Mittelpunktes
Die Koordinaten des Mittelpunktes  lauten
lauten  Ermittle die Koordinaten der Eckpunkte
Ermittle die Koordinaten der Eckpunkte  und
und 
Wir sehen uns die folgende grafische Darstellung des Problems an.
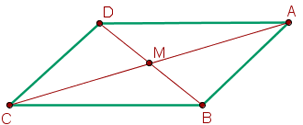
Wir sehen, dass der Punkt  auf einer Seite der Mittelpunkt der Punkte
auf einer Seite der Mittelpunkt der Punkte  und
und  ist. Somit:
ist. Somit:  Auf diese Weise können wir die folgenden Gleichungen verwenden, um die Koordinaten des Punktes
Auf diese Weise können wir die folgenden Gleichungen verwenden, um die Koordinaten des Punktes  zu bestimmen.
zu bestimmen. 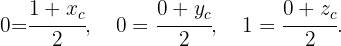
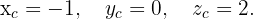
 In ähnlicher Weise gehen wir vor, um die Koordinaten des Punktes
In ähnlicher Weise gehen wir vor, um die Koordinaten des Punktes  zu bestimmen.
zu bestimmen. 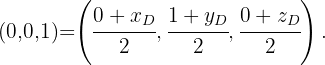 Auf diese Weise lassen sich die Koordinaten des Punktes
Auf diese Weise lassen sich die Koordinaten des Punktes  mit Hilfe der folgenden Gleichungen bestimmen.
mit Hilfe der folgenden Gleichungen bestimmen. 
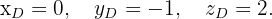

Gegeben ist das Dreieck mit den Eckpunkten 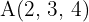 ,
, 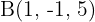 und
und  . Ermittle:
. Ermittle:
1 Die Gleichungen der Seitenhalbierenden des Dreiecks.
2 Die Koordinaten des Schwerpunktes des Dreiecks.
3 Die Koordinaten des Schwerpunkts des Dreiecks, dessen Eckpunkte die Mittelpunkte der Seiten des vorhergehenden Dreiecks sind.
Wir sehen uns die folgende grafische Darstellung des Problems an.
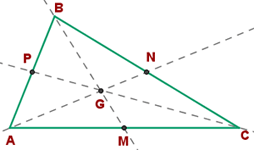
1Um die Seitenhalbierenden des Dreiecks zu finden, müssen wir zunächst die Mittelpunkte der Seiten des Dreiecks bestimmen: 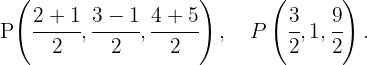

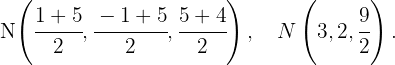 Nun berechnen wir den Richtungsvektor der Seitenhalbierenden
Nun berechnen wir den Richtungsvektor der Seitenhalbierenden 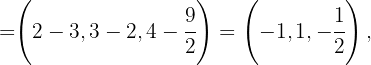
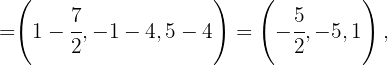
 Mit diesen Gleichungen und den Punkten
Mit diesen Gleichungen und den Punkten  ,
, und
und  können wir die Gleichungen der Seitenhalbierenden aufstellen:
können wir die Gleichungen der Seitenhalbierenden aufstellen: 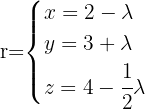
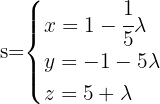
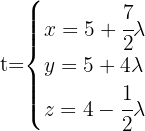
2Die Koordinaten des Schwerpunktes des Dreiecks. 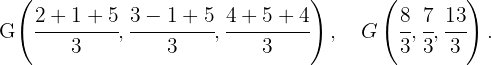
3Die Koordinaten des Schwerpunkts des Dreiecks, dessen Eckpunkte die Mittelpunkte der Seiten des vorhergehenden Dreiecks sind. 
Die Schwerpunkte der Dreiecke stimmen überein.
Ermittle die Gleichung der Geraden, die durch die Punkte  und
und 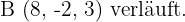 Untersuche, ob der Punkt
Untersuche, ob der Punkt 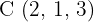 auf einer Geraden mit
auf einer Geraden mit  und
und  liegt.
liegt.
Um die Gerade zu bestimmen, die durch die Punkte  und
und  verläuft, müssen wir den Richtungsvektor bestimmen:
verläuft, müssen wir den Richtungsvektor bestimmen:  Die Gleichung der Geraden lautet
Die Gleichung der Geraden lautet 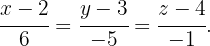 Damit der Punkt que el punto
Damit der Punkt que el punto  auf einer Geraden mit
auf einer Geraden mit  und
und  liegt, muss er auf der Geraden liegen, die durch
liegt, muss er auf der Geraden liegen, die durch  und
und  verläuft.
verläuft.
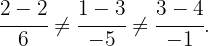
Da  die Gleichungen der Geraden nicht erfüllt, befindet er sich nicht auf einer Geraden mit
die Gleichungen der Geraden nicht erfüllt, befindet er sich nicht auf einer Geraden mit  und
und  .
.
Ermittle die Werte von  , so dass die Punkte
, so dass die Punkte 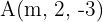 ,
, 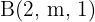 und
und 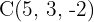 auf einer Geraden liegen, und finde die Gleichungen der Geraden, die diese Punkte enthält.
auf einer Geraden liegen, und finde die Gleichungen der Geraden, die diese Punkte enthält.
Zunächst bestimmen wir den Wert der Vektoren 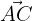 und
und 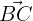 ,
,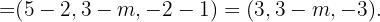
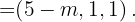 Damit sie auf einer Geraden liegen, muss
Damit sie auf einer Geraden liegen, muss 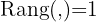 sein. Indem wir die Determinante der niedrigeren Werte der folgenden Matrix gleich 0 setzen, können wir den Wert von
sein. Indem wir die Determinante der niedrigeren Werte der folgenden Matrix gleich 0 setzen, können wir den Wert von  berechnen,
berechnen,
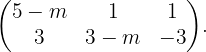
Im Einzelnen haben wir
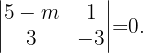
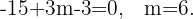
Bestimme den Wert von el valor de  so, dass die Punkte
so, dass die Punkte 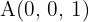 ,
,  ,
, 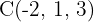 und
und 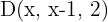 in der gleichen Ebene liegen.
in der gleichen Ebene liegen.
Zunächst ermitteln wir die Vektoren, die durch die Punkte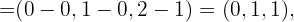 bestimmt sind:
bestimmt sind: 
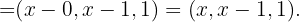 Damit die Punkte in der gleichen Ebene liegen, müssen die durch sie bestimmten Vektoren ebenfalls auf der gleichen Ebene liegen. Das heißt, der Rang der Vektoren ist 2.
Damit die Punkte in der gleichen Ebene liegen, müssen die durch sie bestimmten Vektoren ebenfalls auf der gleichen Ebene liegen. Das heißt, der Rang der Vektoren ist 2.
Damit der Rang gleich 2 ist, muss die Determinante der Komponenten der Vektoren 0 sein.
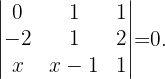
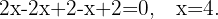
Welche Beziehung muss zwischen den Parametern  ,
,  und
und  geprüft werden, damit die Punkte
geprüft werden, damit die Punkte  ,
, 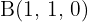 ,
, 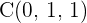 und
und  in der gleichen Ebene liegen?
in der gleichen Ebene liegen?
Zunächst ermitteln wir die Vektoren, die durch die Punkte  bestimmt sind:
bestimmt sind: 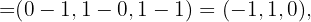
 Damit die Punkte in der gleichen Ebene liegen, müssen die durch sie bestimmten Vektoren ebenfalls in der gleichen Ebene liegen, d. h. der Rang der Vektoren muss 2 sein.
Damit die Punkte in der gleichen Ebene liegen, müssen die durch sie bestimmten Vektoren ebenfalls in der gleichen Ebene liegen, d. h. der Rang der Vektoren muss 2 sein.
Damit der Rang gleich 2 ist, muss die Determinante der Komponenten der Vektoren gleich 0 sein.
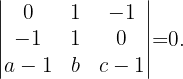
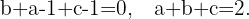
Berechne den Wert von a, so dass die Punkte 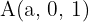 ,
,  ,
, 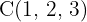 und
und 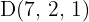 in der gleichen Ebene liegen. Berechne auch die Gleichung der Ebene, die sie enthält.
in der gleichen Ebene liegen. Berechne auch die Gleichung der Ebene, die sie enthält.
Wir legen den Punkt  fest und berechnen die folgenden Vektoren mit Ausgangspunkt
fest und berechnen die folgenden Vektoren mit Ausgangspunkt  ,
,
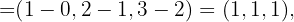
 Für diese Vektoren muss
Für diese Vektoren muss 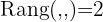 gelten, weshalb die folgende Determinante 0 sein muss,
gelten, weshalb die folgende Determinante 0 sein muss, 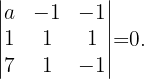
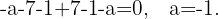
Um schließlich die Gleichung der Ebene zu finden, betrachten wir die folgenden Vektoren und die folgende Determinante

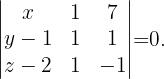
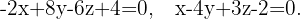
Mit KI zusammenfassen:


