Schreibe alle möglichen Formen der Gleichung der Geraden, die durch die Punkte  und
und  verläuft.
verläuft.
Schreibe alle möglichen Formen der Gleichung der Geraden, die durch die Punkte  und
und 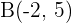 verläuft.
verläuft.
Lösung:
Wir wissen, dass die Gerade durch die Punkte  und
und  verläuft. Der Vektor, der diese zwei Punkte vereint, ist daher:
verläuft. Der Vektor, der diese zwei Punkte vereint, ist daher:

Mit diesen Werten können wir die Geradengleichungen erstellen.
Gleichung der Geraden, die durch 2 Punkte verläuft:

Vektorielle Gleichung:

Geradengleichungen in Parameterform:

Parameterfreie Form:

Allgemeine Geradengleichung:

Explizite Darstellung:

Punktsteigunsform:

Gegeben ist ein Parallelogramm  , dessen Eckpunkte
, dessen Eckpunkte  bekannt sind. Bestimme die Koordinaten des Eckpunktes D.
bekannt sind. Bestimme die Koordinaten des Eckpunktes D.
Gegeben ist ein Parallelogramm  , dessen Eckpunkte
, dessen Eckpunkte  bekannt sind. Bestimme die Koordinaten des Eckpunktes
bekannt sind. Bestimme die Koordinaten des Eckpunktes  .
.
Lösung:
Bevor wir die Koordinaten des Brennpunktes bestimmen, sehen wir uns die folgende Abbildung an:
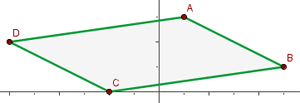
Wir wissen, dass der Vektor, der von  nach
nach  verläuft, gleich dem Vektor sein muss, der von
verläuft, gleich dem Vektor sein muss, der von  nach
nach  verläuft. Das heißt:
verläuft. Das heißt:

Wir berechnen:

 ist hierbei die Koordinate x des Punktes
ist hierbei die Koordinate x des Punktes  und
und  ist die Koordinate y. Somit erhalten wir:
ist die Koordinate y. Somit erhalten wir:

Der Punkt  ist also
ist also

Bestimme, um welche Art von Dreieck es sich bei dem Dreieck mit den folgenden Punkten handelt:  und
und 
Bestimme, um welche Art von Dreieck es sich bei dem Dreieck mit den folgenden Punkten handelt: 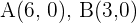 und
und 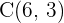 .
.
Lösung:
Um das Dreieck zu beschreiben, müssen wir zunächst den Abstand zwischen den einzelnen Seiten des Dreiecks berechnen. Dies machen wir wie folgt:



Wir stellen fest, dass gilt:
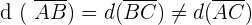
Das Dreieck ist also gleichschenklig. Außerdem gilt

Daher ist das Dreieck außerdem rechtwinklig. Das sehen wir anhand der folgenden Abbildung:
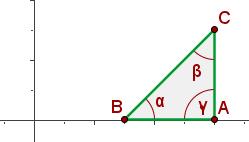
Ermittle die Steigung und die Ordinate im Ursprung der Geraden  .
.
Ermittle die Steigung und die Ordinate im Ursprung der Geraden:  .
.
Lösung:
Wir haben die Gleichung  . Wir bestimmen
. Wir bestimmen  :
:

Wir sehen, dass die Steigung wie folgt lautet:
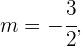
Die Ordinate im Ursprung ist:

Untersuche die relative Lage der Geraden der Gleichungen:
a 
b 
c 
d 
Wir stellen fest, dass die Koeffizienten der Geraden 1 und 2 proportional sind:

Die Geraden 1 und 2 sind also deckungsgleich (es handelt sich um dieselbe Gerade).
Wir stellen ebenfalls fest, dass die Koeffizienten von  und
und  der Geraden 1 und 3 proportional sind, allerdings sind die konstanten Glieder nicht proportional:
der Geraden 1 und 3 proportional sind, allerdings sind die konstanten Glieder nicht proportional:

Die Geraden 1 und 3 sind also parallel. Somit sind auch die Geraden 2 und 3 parallel.
Und schließlich stellen wir fest, dass die Koeffizienten von  und
und  der Geraden 4 nicht proportional zu den Koeffizienten einer anderen Gleichung sind:
der Geraden 4 nicht proportional zu den Koeffizienten einer anderen Gleichung sind:

Die Gerade 4 ist also eine Sekante der Geraden 1, 2 und 3.
Bestimme die Gleichung der Geraden  , die durch den Punkt
, die durch den Punkt  verläuft und parallel zu der Geraden
verläuft und parallel zu der Geraden  ist.
ist.
Wir sehen uns die folgende Abbildung zweier paralleler Geraden an:
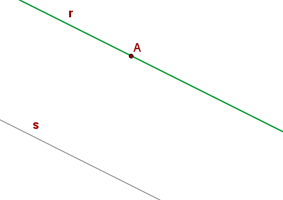
Wir wissen, dass zwei Geraden parallel sind, wenn ihre Steigung gleich ist:

Deshalb hat die Gerade  die folgende Form (Punkt-Steigung):
die folgende Form (Punkt-Steigung):

Wir setzen gleich 0 und erhalten:

Gegeben ist ein Viereck  mit den Eckpunkten
mit den Eckpunkten  und
und 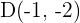 . Beweise, dass es sich um ein Parallelogramm handelt und bestimme seinen Mittelpunkt.
. Beweise, dass es sich um ein Parallelogramm handelt und bestimme seinen Mittelpunkt.
Damit das Viereck ein Parallelogramm ist, muss Folgendes gelten:  und
und 
Somit:


Deshalb gilt  . Außerdem:
. Außerdem:

Das Viereck ist also ein Parallelogramm.
Nun müssen wir den Mittelpunkt bestimmen. Wir wissen, dass sich die Diagonalen im Mittelpunkt (und dies ist die Mitte des Parallelogramms) schneiden. Es genügt also, den Mittelpunkt einer der Diagonalen zu berechnen. Der Mittelpunkt der Diagonalen \bar{AC} ist

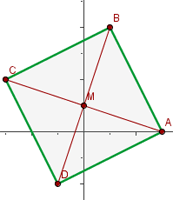
Der Mittelpunkt ist also  . Wir sehen uns die Abbildung des Parallelogramms an:
. Wir sehen uns die Abbildung des Parallelogramms an:
Bestimme die Gleichung der Geraden, die durch den Punkt  verläuft und parallel zu der Geraden ist, die die Punkte
verläuft und parallel zu der Geraden ist, die die Punkte  und
und  verbindet.
verbindet.
Wenn  die Gerade ist, die die Punkte verbindet, wissen wir nun, dass die gesuchte Gerade
die Gerade ist, die die Punkte verbindet, wissen wir nun, dass die gesuchte Gerade  parallel zu
parallel zu  ist. Ihre Steigung ist daher gleich:
ist. Ihre Steigung ist daher gleich:
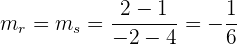
Wenn wir die Punktsteigungsform der Geraden anwenden, ist die Gleichung der Geraden  :
:
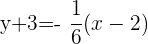
Die Gleichung der Geraden  erhalten wir, indem wir null setzen:
erhalten wir, indem wir null setzen:

Die Punkte  und
und  sind Eckpunkte eines gleichschenkligen Dreiecks
sind Eckpunkte eines gleichschenkligen Dreiecks  . Der Mittelpunkt
. Der Mittelpunkt  dieses Dreiecks liegt auf der Geraden
dieses Dreiecks liegt auf der Geraden  , wobei
, wobei  und
und  gleich lange Seiten sind. Berechne die Koordinaten des Eckpunktes
gleich lange Seiten sind. Berechne die Koordinaten des Eckpunktes  .
.
Wir schreiben die Koordinaten des Punktes  als
als  . Da
. Da  , muss gelten:
, muss gelten:

Wenn wir  bestimmen, erhalten wir
bestimmen, erhalten wir

Außerdem sind die Seiten  und
und  gleich lang, da gilt:
gleich lang, da gilt: 

Wir quadrieren und erhalten:

Wir setzen den Wert  ein und erhalten:
ein und erhalten:

Wir lösen das Polynom und die "quadratische" Gleichung (die quadratischen Terme fallen am Ende weg). Wir erhalten:

Zum Schluss setzen wir den Wert für  in die Gleichung ein, um
in die Gleichung ein, um  zu bestimmen:
zu bestimmen:

Der Punkt ist also  . Folgende Abbildung zeigt das Dreieck:
. Folgende Abbildung zeigt das Dreieck:
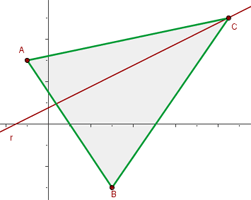
Die Gerade  verläuft durch den Punkt
verläuft durch den Punkt  und ist parallel zu der Geraden
und ist parallel zu der Geraden  . Berechne
. Berechne  und
und  .
.
Wir wissen, dass  für den Punkt
für den Punkt  . Wenn wir also die Koordinaten des Punktes einsetzen, ist die Gleichung immer noch erfüllt:
. Wenn wir also die Koordinaten des Punktes einsetzen, ist die Gleichung immer noch erfüllt:

Außerdem wissen wir, dass  . Die Koeffizienten sind somit proportional:
. Die Koeffizienten sind somit proportional:

Somit: 
Gegeben ist das Dreieck  mit den Punkten
mit den Punkten  und
und  . Berechne die Gleichung der Seitenhalbierenden, die durch den Eckpunkt
. Berechne die Gleichung der Seitenhalbierenden, die durch den Eckpunkt  verläuft.
verläuft.
Wir haben das folgende Dreieck und möchten die eingezeichnete Seitenhalbierende berechnen:
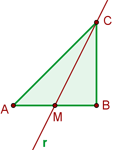
Wir wissen, dass die Seitenhalbierende durch den Mittelpunkt der Seite  verläuft. Daher berechnen wir die Koordinaten dieses Punktes (diesen nennen wir
verläuft. Daher berechnen wir die Koordinaten dieses Punktes (diesen nennen wir  ):
):

Nun schreiben wir die Gleichung der Geraden, die durch  und
und  verläuft (wir wenden die Formel für die Gerade, die durch zwei Punkte verläuft, an):
verläuft (wir wenden die Formel für die Gerade, die durch zwei Punkte verläuft, an):
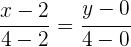
Wir vereinfachen und erhalten die folgende Gleichung:

Gegeben ist ein Parallelogramm, dessen Eckpunkt  sowie der Schnittpunkt der Diagonalen,
sowie der Schnittpunkt der Diagonalen,  , bekannt ist. Wir wissen auch, dass ein weiterer Eckpunkt im Koordinatenursprung liegt. Berechne:
, bekannt ist. Wir wissen auch, dass ein weiterer Eckpunkt im Koordinatenursprung liegt. Berechne:
a Die anderen Eckpunkte.
b Die Gleichungen der Diagonalen.
c Die Länge der Diagonalen.
Wir lösen jede der gestellten Aufgaben:
a Die anderen Eckpunkte:
Wir wissen, dass  der Mittelpunkt von
der Mittelpunkt von  ist:
ist:

Daraus ergibt sich:

Somit ist  . Und somit ist
. Und somit ist  also der Mittelpunkt von
also der Mittelpunkt von  :
:

Daraus ergibt sich:

Wir erhalten  . Die anderen Eckpunkte sind also die Punkte
. Die anderen Eckpunkte sind also die Punkte  und
und  .
.
b Die Gleichungen der Diagonalen.
In diesem Fall müssen wir nur die Formel der Gleichung der Geraden, die durch zwei Punkte verläuft, anwenden. Als Erstes für die Diagonale  :
:

Wir vereinfachen und erhalten  . Für die Diagonale
. Für die Diagonale  erhalten wir:
erhalten wir:

Wir vereinfachen und erhalten  .
.
c Die Länge der Diagonalen.
Um die Länge der Diagonalen zu berechnen, genügt es, den Abstand zwischen den entsprechenden Eckpunkten zu ermitteln. Für die Diagonale  erhalten wir:
erhalten wir:

Für die Länge der Diagonalen  gilt:
gilt:

Grafisch dargestellt sieht das Parallelogramm wie folgt aus:
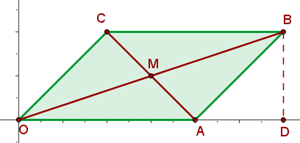
Mit KI zusammenfassen:



