Kapitel
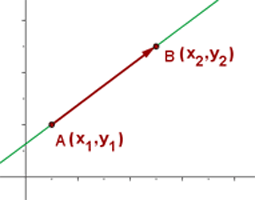
Wie können wir die Geradengleichung erstellen, wenn zwei Punkte bekannt sind?
Die Punkte 
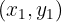und 
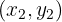bestimmen eine Gerade 
.
Ein Richtungsvektor der Geraden ist:
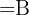
Mit den Komponenten:
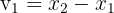und 
Wir setzen diese Werte in die folgende Formel ein:
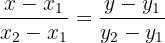
Wir können die Gleichung der Geraden ermitteln.
Die Geradengleichung ermitteln, wenn zwei Punkte bekannt sind
Bestimme die Gleichung der Geraden, die durch
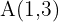und 
verläuft.
Wir setzen die Werte ein:
Somit lautet die Gleichung der Geraden:
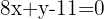
Zwei Punkte auf einer Geraden bestimmen, wenn die Gleichung bekannt ist
Wenn wir die Gleichung einer Geraden kennen, ist es sehr einfach, die Punkte zu finden, die zu ihr gehören. Wir denken daran, dass die Gleichung der Geraden in verschiedenen Formen geschrieben werden kann: allgemeine Form, Parameterform oder Punktsteigungsform zum Beispiel.
Um die Punkte auf der Geraden zu bestimmen, ist es am besten, die Punktsteigungsform zu verwenden und eine Tabelle (Wertetabelle) zu erstellen, in der wir viele Koordinaten (Punkte) finden, die zu der Geraden gehören.
Beispiel:
Allgemeine Form : 
Wir können sie in ihrer Punktsteigungsform schreiben (wir bestimmen y) :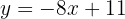 
Nun können wir 
einen beliebigen Wert zuweisen und den y entsprechenden Wert ermitteln. Sehen wir uns folgende Tabelle an:
| P1 | P2 | Verfügbar | |
|---|---|---|---|
| Hefte | 2 | 3 | 600 |
| Mappen | 1 | 1 | 500 |
| Kugelschreiber | 2 | 1 | 400 |
Eine weitere einfache Möglichkeit, schnell 2 Punkte auf der Geraden zu bestimmen, besteht darin, sich zu merken, was die einzelnen Elemente der Punktsteigungsform bedeuten:
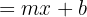
ist hierbei die Steigung der Geraden und 
ist die Koordinate des Punktes, an dem die Gerade die 
-Achse schneidet. So sehen wir schnell, dass ein Punkt auf der Geraden der Punkt 
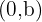ist.
Nun nehmen wir an, dass in unserer Gleichung die Variable 
ist und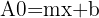 
. Wir bestimmen :
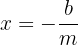
Dieser Wert wird als 
bezeichnet und ist der Wert, an dem die Gerade die -Achse schneidet. So sehen wir schnell, dass ein Punkt auf der Geraden der Punkt 
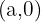ist.
In unserer Beispielgleichung würden wir also die Punkte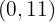 
und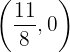 
erhalten.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
