Relative Lage dreier Ebenen und Koeffizientenmatrix
Gegeben sind die Ebenen:
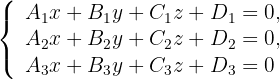
Sowie:
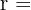ist der Rang der Koeffizientenmatrix.
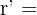ist der Rang der erweiterten Matrix.
Die relative Lage der drei Ebenen ist in der folgenden Tabelle angegeben:
 |  | Lage | |
|---|---|---|---|
 | | 1. Ebenen schneiden sich an einem Punkt | |
 | |  | 2.1 Jeweils zwei Ebenen schneiden sich. 2.2 Zwei Ebenen sind parallel, die dritte Ebene schneidet die zwei Ebenen. |
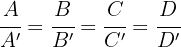| | |  | 3.1 Drei Ebenen schneiden sich und besitzen eine gemeinsame Schnittgerade. 3.2 Zwei Ebenen sind identisch, die dritte Ebene schneidet die 2 Ebenen. |
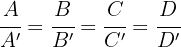 | | | 4.1 Die drei Ebenen sind zueinander parallel. 4.2 Die Ebenen sind zueinander parallel, zwei Ebenen sind identisch. |
| | | 5. Die drei Ebenen sind identisch. |
Ebenen schneiden sich an einem Punkt
Wenn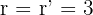 
, schneiden sich die Ebenen an einem Punkt. Das bedeutet, dass das Gleichungssystem, das die drei Ebenen bilden eine einzige Lösung
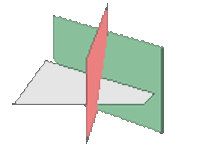
Wenn 
und 
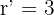, gibt es zwei Möglichkeiten, wie sich die drei Ebenen schneiden können
Zwei Ebenen schneiden sich
Wenn und 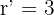, kann es sein, dass sich jeweils zwei Ebenen schneiden und eine prismenförmige Oberfläche bilden. In diesem Fall hat das Gleichungssystem keine Lösung.
Zwei Ebenen sind parallel, die dritte Ebene schneidet
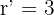Wenn und , kann es sein, dass zwei Ebenen parallel sind und die dritte Ebene die beiden parallelen Ebenen schneidet. In diesem Fall hat das Gleichungssystem keine Lösung und zwei Zeilen der Koeffizientenmatrix sind proportional.
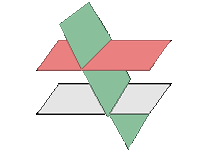
Wenn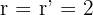 
, gibt es zwei Möglichkeiten, wie sich die drei Ebenen schneiden
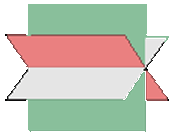
Drei unterschiedliche Ebenen schneiden sich
Wenn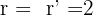 
, kann es sein, die drei Ebenen unterschiedlich sind und sich schneiden, sie jedoch eine gemeinsame Schnittgerade haben. In diesem Fall hat das Gleichungssystem unendlich viele Lösungen.
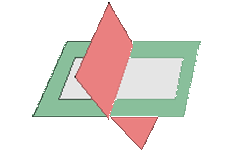
Zwei Ebenen sind identisch, eine Ebene schneidet
Wenn 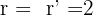, kann es sein, dass zwei Ebenen identisch sind und die dritte Ebene die Ebenen schneidet. In diesem Fall hat das Gleichungssystem unendlich viele Lösungen und zwei Zeilen der erweiterten Matrix sind proportional.
Wenn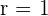 
und 
, gibt es zwei Möglichkeiten, wie sich die drei Ebenen schneiden können
Parallele Ebenen
Wenn 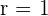y , kann es sein, dass die drei Ebenen zueinander parallel sind. In diesem Fall hat das Gleichungssystem keine Lösung.
Parallele Ebenen, davon sind zwei Ebenen identisch
Wenn 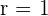und , kann es sein, dass zwei Ebenen identisch und zur dritten Ebene Ebene parallel sind. In diesem Fall hat das Gleichungssystem keine Lösung und zwei Zeilen der erweiterten Matrix sind proportional.
Identische Ebenen
Wenn 
, sind alle drei Ebenen identisch. In diesem Fall hat das Gleichungssystem unendlich viele Lösungen.
Beispiele mit Lösungen
Ermittle die relative Lage der Ebenen:
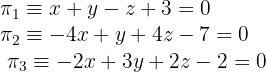
1Wir schreiben das Gleichungssystem
2Wir berechnen den Rang der Koeffizientenmatrix 
Dazu berechnen wir die Determinante von
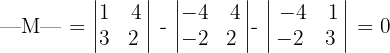
Wir berechnen die Determinante der Untermatrix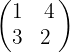 
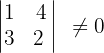
Somit
3Wir berechnen den Rang der erweiterten Koeffizientenmatrix 
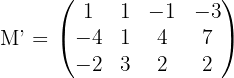
Dazu berechnen wir die Determinante der Untermatrix
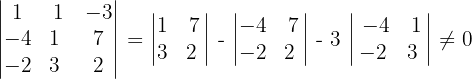
Somit .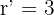
Da die Ebenen nicht zueinander parallel sind, gilt und 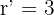. Daraus ergibt sich, dass die drei Ebenen zwei mal zwei Sekanten sind und eine prismenförmige Fläche bilden.
1Wir schreiben das Gleichungssystem
2Wir berechnen den Rang der Koeffizientenmatrix
Dazu berechnen wir die Determinante von
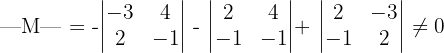
Somit
3Wir berechnen den Rang der erweiterten Koeffizientenmatrix
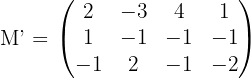
Wir berechnen die Determinante der Untermatrix , die ungleich 0 ist. Somit .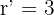
Daraus folgt, dass sich die drei Ebenen an einem Punkt schneiden.
1Wir schreiben das Gleichungssystem
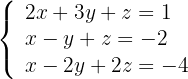
2Wir berechnen den Rang der Koeffizientenmatrix
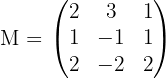
Dazu berechnen wir die Determinante von
Wir berechnen die Determinante der Untermatrix 
Somit
3Wir berechnen den Rang der erweiterten Koeffizientenmatrix
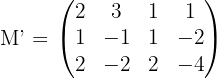
Da die zweite und dritte Zeile ein Vielfaches voneinander sind, hat jede 3-mal-3-Untermatrix die Determinante 0. Wir berechnen die Determinante der Untermatrix
Somit
Daraus ergibt sich, dass die zweite und die dritte Ebene identisch sind und die erste Ebene diese Ebenen schneidet.
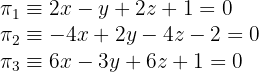
1Wir schreiben das Gleichungssystem
2Wir berechnen den Rang der Koeffizientenmatrix
Da alle drei Zeilen ein Vielfaches voneinander sind, ist die Determinante dieser Matrix und aller ihrer Untermatrizen der Größe 2 gleich 0. Wir berechnen die Determinante von
Somit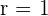
3Wir berechnen den Rang der erweiterten Koeffizientenmatrix
Da die erste und die zweite Zeile ein Vielfaches voneinander sind, hat jede 3-mal-3-Untermatrix die Determinante 0. Wir berechnen die Determinante der Untermatrix
Somit
Daraus lässt sich schließen, dass die erste und die zweite Ebene identisch sind und die dritte Ebene parallel zu ihnen ist.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
