Kapitel

Wie sind der Schwerpunkt und die Mediane eines Dreiecks definiert?
- Als Median eines Dreiecks wird die Gerade bezeichnet, die vom Mittelpunkt einer Dreiecksseite zu ihrem gegenüberliegenden Scheitelpunkt verläuft.
- Der Schwerpunkt des Dreiecks ist der Punkt, an dem sich die drei Mediane schneiden.
- Der Schwerpunkt wird durch den Buchstaben G repräsentiert.
Eigenschaften des Schwerpunkts
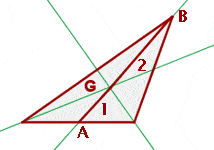
- Der Schwerpunkt teilt jeden Median in zwei Segmente.
- Das Segment, das den Schwerpunkt mit dem Scheitelpunkt verbindet, ist doppelt so lang wie das Segment, das den Schwerpunkt mit dem Mittelpunkt der gegenüberliegenden Dreiecksseite verbindet.
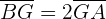
- Der Schwerpunkt (auch "Massenmittelpunkt") wird als solcher bezeichnet, da um ihn herum die Masse eines Objekts genau gleich verteilt ist. Ein Dreieck aus Karton kann man zum Beispiel auf einer Fingerspitze im Gleichgewicht halten, indem man die Fingerspitze genau unter seinem Schwerpunkt platziert.
Koordinaten des Schwerpunkts
Gegeben sei ein Dreieck mit den Koordinaten:
 ,
, 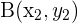 ,
, 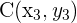
Die Koordinaten des Schwerpunkts 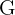 sind:
sind:
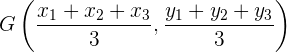
Gemischte Aufgaben - Ermittle die Gleichungen für die Mediane und den Schwerpunkt
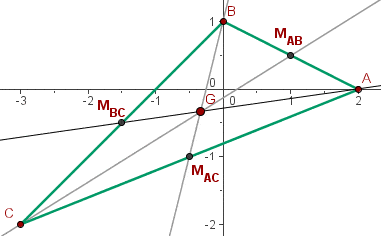
Ermittle die Gleichungen der Mediane und des Schwerpunkts eines Dreiecks mit den Scheitelpunkten:
 ,
,  und
und 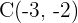 .
.
Was du für die Berechnung wissen solltest:
Sind zwei Punkte 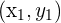 und
und 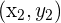 gegeben, so sind die Koordinaten des Mittelpunkts:
gegeben, so sind die Koordinaten des Mittelpunkts:
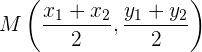
Die Gleichung einer Geraden, die durch zwei Punkte 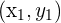 und
und 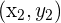 verläuft, ist:
verläuft, ist:
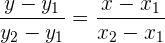
Ermittle die Koordinaten des Schwerpunkts anhand der Koordinaten des Dreiecks (s. Formel im vorherigen Abschnitt)
Gleichung des Medians, der durch den Punkt A und den Mittelpunkt der Geraden BC verläuft
Zuerst wird der Mittelpunkt von BC gesucht:

Da der Median durch die Punkte 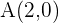 und
und  verläuft, zieht man sich die Formel für die Geradengleichung anhand zweier Punkte zuhilfe
verläuft, zieht man sich die Formel für die Geradengleichung anhand zweier Punkte zuhilfe
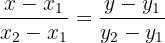
Setze die Daten der Koordinaten ein und löse auf
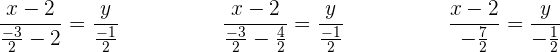
Da eine Division vom Brüchen vorliegt, kann die Gleichung wie folgt umgeschrieben werden
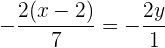
Teile die gesamte Gleichung durch -2
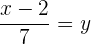
Multipliziere mit 7 und bringe alle Terme auf die linke Seite
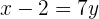
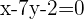
Gleichung des Medians, der durch den Punkt b und den Mittelpunkt der Geraden AC verläuft
Wie im vorherigen Rechenverfahren wird nun der Mittelpunkt von AC ermittelt

Da der Median durch die Punkte 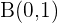 und
und  verläuft, zieht man sich die Formel für die Geradengleichung anhand zweier Punkte zuhilfe
verläuft, zieht man sich die Formel für die Geradengleichung anhand zweier Punkte zuhilfe
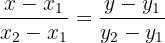
Setze die Daten der Koordinaten ein und löse auf

Da eine Division vom Brüchen vorliegt, kann die Gleichung wie folgt umgeschrieben werden

Multipliziere die Gleichung mit -2, um den Bruch aufzulösen und bringe alle Terme auf eine Seite

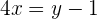
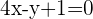
Gleichung des Medians, der durch den Punkt C und den Mittelpunkt der Geraden AB verläuft
Der Mittelpunkt von AB ist wie folgt festgelegt:
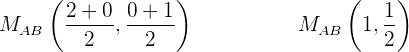
Da der Median durch die Punkte 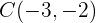 und
und  verläuft, zieht man sich die Formel für die Geradengleichung anhand zweier Punkte zuhilfe
verläuft, zieht man sich die Formel für die Geradengleichung anhand zweier Punkte zuhilfe
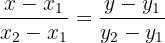
Setze die Daten der Koordinaten ein und löse auf

Da eine Division vom Brüchen vorliegt, kann die Gleichung wie folgt umgeschrieben werden
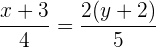
Durch multiplizieren mit 4 löst man den Nenner auf der linken Seite auf. Gleichermaßen löst man den Nenner auf der rechten Seite durch multiplizieren mit 5.
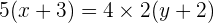
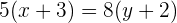
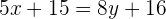
Bringe alle Terme auf die linke Seite
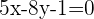
Mit KI zusammenfassen:













