Kapitel

Vektorielle Formen der Ebenengleichung
Um eine Ebene im Raum zu bilden, muss man einen Punkt  und zwei Vektoren kennen, die eine Fläche bilden, d.h. linear unabhängig voneinander sind.
und zwei Vektoren kennen, die eine Fläche bilden, d.h. linear unabhängig voneinander sind.
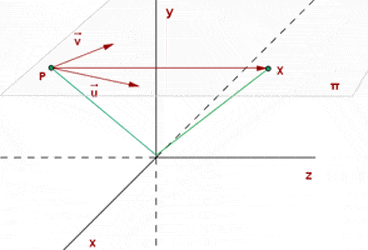
Ein Punkt 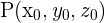 ist dann Teil der Ebene
ist dann Teil der Ebene  , wenn der Vektor
, wenn der Vektor 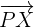 koplanar zu den beiden Vektoren
koplanar zu den beiden Vektoren 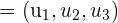 und
und  ist, das heißt, wenn er linear abhängig von
ist, das heißt, wenn er linear abhängig von  und
und  ist.
ist.
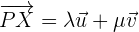
Die Koordinatenschreibweise lautet wie folgt:

Ebenengleichung in Parameterform
Durch Umformen der vektoriellen Ebenengleichung erhält man die Gleichung:

Damit diese Gleichung aufgeht, muss sie Folgendes erfüllen:

Die beiden Gleichungen sind auch als Gleichungen der Geraden in Parameterform bekannt.
Allgemeine Ebenengleichung
Ein Punkt liegt dann auf der Ebene  , wenn folgendes Gleichungssystem lösbar ist:
, wenn folgendes Gleichungssystem lösbar ist:
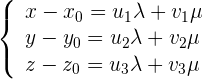
Dieses Gleichungssystem muss für  und
und  eine Lösung besitzen, daher muss die Determinante der erweiterten Matrix des Gleichungssystems, die die konstanten Glieder enthält, gleich Null sein.
eine Lösung besitzen, daher muss die Determinante der erweiterten Matrix des Gleichungssystems, die die konstanten Glieder enthält, gleich Null sein.
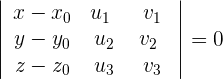
Durch Auflösen der Determinante erhält man:

Definiere die Werte für die Koordinaten:

Setze ein:
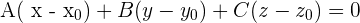
Vereinfache und definiere für  den Wert:
den Wert:

Man erhält die allgemeine Ebenengleichung:
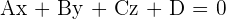
Ebenengleichung in Koordinatenform
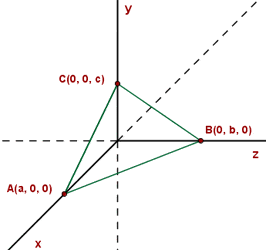
Anhand der Punkte 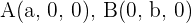 und
und  sei die folgende Gleichung in Koordinatenform gegeben:
sei die folgende Gleichung in Koordinatenform gegeben:
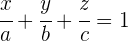
Dabei ist
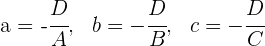
Gemischte Aufgaben
Stelle die Gleichung der Ebene in Parameterform auf, die durch den Punkt 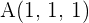 verläuft und deren Richtungsvektoren
verläuft und deren Richtungsvektoren 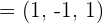 und
und  sind
sind
1 Setze den Punkt sowie die Richtungsvektoren in die Formel der parametrischen Ebenengleichung ein und du erhältst
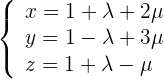
2 Setze den Punkt sowie die Richtungsvektoren in die allgemeine Ebenengleichung ein und du erhältst
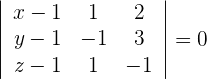
Durch Auflösen der Determinante erhält man:
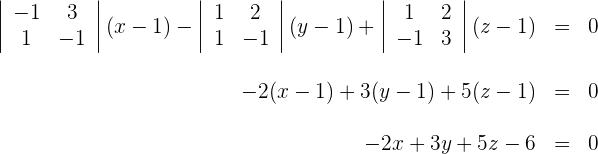
Stelle die Gleichungen der Ebene in Parameterform auf, die durch die Punkte 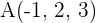 und
und  verlaufen und den Vektor
verlaufen und den Vektor  enthalten
enthalten
1 Ein Richtungsvektor ist bereits gegeben. Der andere Vektor wird wie folgt gebildet:
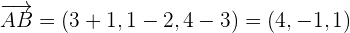
2 Setze den Punkt sowie die Richtungsvektoren in die Formel der parametrischen Ebenengleichung ein und du erhältst
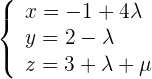
3 Setze den Punkt sowie die Richtungsvektoren in die allgemeine Ebenengleichung ein und du erhältst
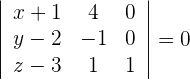
Durch Auflösen der Determinante erhält man:
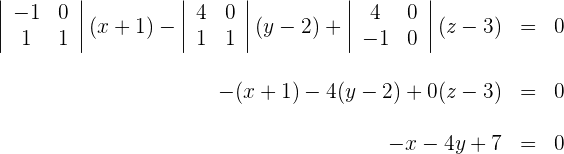
Stelle die Gleichungen der Ebene in Parameterform auf, die durch die Punkte 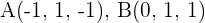 und
und  verläuft
verläuft
1 Ermittle die Richtungsvektoren
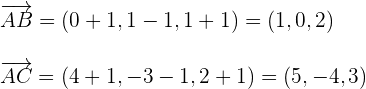
2 Setze den Punkt sowie die Richtungsvektoren in die Formel der parametrischen Ebenengleichung ein und du erhältst
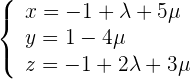
3 Setze den Punkt sowie die Richtungsvektoren in die allgemeine Ebenengleichung ein und du erhältst
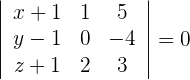
Durch Auflösen der Determinante erhält man:

Überprüfe anhand der Ebenengleichung in Parameterform, ob die Punkte  und
und 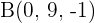 Teil der Ebene
Teil der Ebene  sind
sind
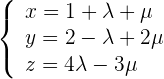
1 Auf Basis der Ebenengleichung in Parameterform erhält man einen Punkt auf der Ebene sowie die Richtungsvektoren
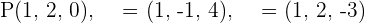
2 Setze den Punkt sowie die Richtungsvektoren in die allgemeine Ebenengleichung ein und du erhältst
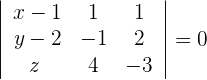
Durch Auflösen der Determinante erhält man:
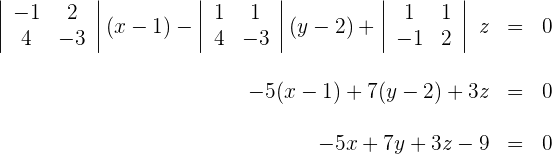
3 Setze die Punkte in die allgemeine Ebenengleichung ein und du erhältst
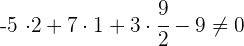 , folglich ist
, folglich ist 
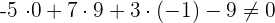 , folglich ist
, folglich ist 
Stelle die Gleichungen der Ebene in Koordinatenform auf, die durch die Punkte 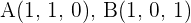 und
und 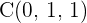 verläuft.
verläuft.
1 Ermittle die Richtungsvektoren

2 Setze den Punkt sowie die Richtungsvektoren in die allgemeine Ebenengleichung ein und du erhältst
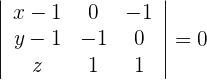
Durch Auflösen der Determinante erhält man:
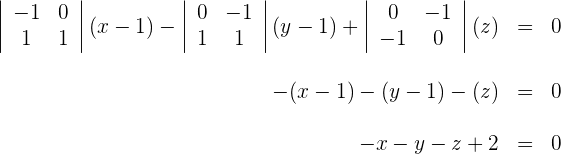
3 Die Gleichung in Koordinatenform lautet
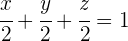
Stelle die Gleichung für eine Ebene auf, die durch den Punkt 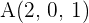 verläuft und die Gerade mit folgender Gleichung enthält
verläuft und die Gerade mit folgender Gleichung enthält
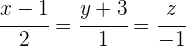
1 Anhand der Geradengleichung erhält man einen Punkt auf der Ebene sowie einen Richtungsvektor

2 Anhand der beiden Punkte kann der andere Richtungsvektor ermittelt werden

3 Setze den Punkt sowie die Richtungsvektoren in die allgemeine Ebenengleichung ein und du erhältst

Durch Auflösen der Determinante erhält man:
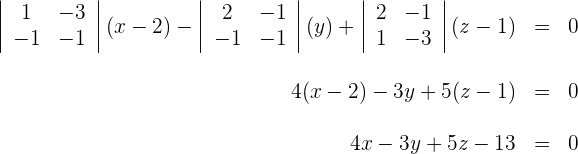
Stelle die Gleichung für eine Ebene auf, die durch die Punkte 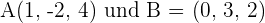 verläuft und parallel zur Geraden mit folgender Gleichung liegt
verläuft und parallel zur Geraden mit folgender Gleichung liegt

1 Anhand der Geradengleichung erhält man einen Richtungsvektor
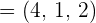
2 Anhand der beiden Punkte kann der andere Richtungsvektor ermittelt werden

3 Setze den Punkt sowie die Richtungsvektoren in die allgemeine Ebenengleichung ein und du erhältst
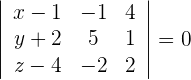
Durch Auflösen der Determinante erhält man:
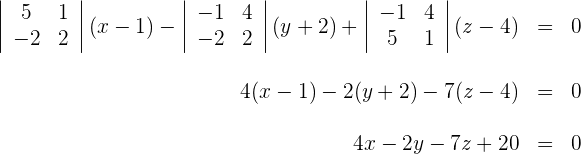
Gegeben seien die Geraden
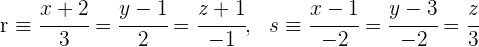
Stelle die Gleichung einer Ebene auf, die  enthält und parallel zu
enthält und parallel zu  verläuft
verläuft
1 Anhand der Geradengleichungen erhält man einen Punkt und die beiden Richtungsvektoren

2 Setze den Punkt sowie die Richtungsvektoren in die allgemeine Ebenengleichung ein und du erhältst

Durch Auflösen der Determinante erhält man:
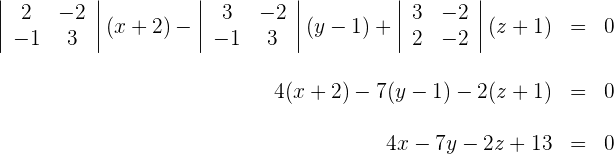
Mit KI zusammenfassen:













