Kapitel

Vektorgleichung
In diesem Abschnitt erfährst du, wie du die Punkte 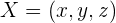 , die zu einer Ebene
, die zu einer Ebene  gehören, als Vektoren darstellst.
gehören, als Vektoren darstellst.
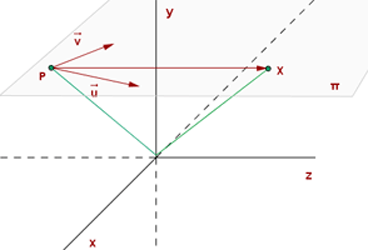
Hierfür benötigen wir einen festen Punkt auf der Ebene 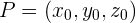 und zwei Vektoren mit unterschiedlichen Richtungen, nämlich
und zwei Vektoren mit unterschiedlichen Richtungen, nämlich 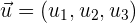 und
und 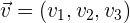 . Diese Vektoren werden Richtungsvektoren genannt.
. Diese Vektoren werden Richtungsvektoren genannt.
Die Vektoren  und
und  sind Richtungsvektoren, da sie die Richtungen zur Festlegung der Punkte
sind Richtungsvektoren, da sie die Richtungen zur Festlegung der Punkte  auf der Ebene
auf der Ebene  vorgeben.
vorgeben.
Die Vektorgleichung wird wie folgt aufgestellt:
- Wir nehmen einen Punkt
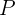 als Referenzpunkt der Ebene
als Referenzpunkt der Ebene 
- Wir nehmen einen Vektor auf der Ebene
 , der von
, der von 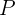 nach
nach  verläuft. Dieser Vektor kann wie folgt festgelegt werden
verläuft. Dieser Vektor kann wie folgt festgelegt werden

- Da
 und
und  ebenfalls zu
ebenfalls zu  gehören und nicht dieselbe Richtung haben, ist es möglich, jeweils die Skalare
gehören und nicht dieselbe Richtung haben, ist es möglich, jeweils die Skalare 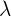 und
und 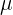 zu bestimmen. So können die Vektoren
zu bestimmen. So können die Vektoren  und
und 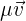 gebildet werden, deren Summe
gebildet werden, deren Summe 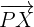 ist. Das heißt:
ist. Das heißt:
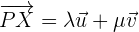
Wir erhalten

Das heißt:

Wir erhalten die Gleichung der Elemente der Ebene  in Vektorform:
in Vektorform:

Ebenengleichungen in Parameterform
Wenn wir mit der Vektorgleichung der Ebene arbeiten, erhalten wir die Gleichheit:
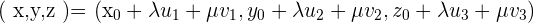
Diese Gleichheit ist gegeben, wenn:
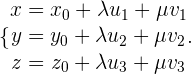
So erhalten wir die Ebenengleichungen in Parameterform.
Allgemeine Form oder implizite Darstellung
Ein Punkt  befindet sich auf der Ebene
befindet sich auf der Ebene  , wenn das System eine Lösung hat:
, wenn das System eine Lösung hat:
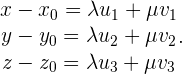
Dieses System muss für die Unbekannten 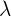 und
und 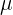 eindeutig lösbar sein· Daher muss die Determinante der erweiterten Matrix des Systems mit der Spalte der konstanten Glieder 0 sein.
eindeutig lösbar sein· Daher muss die Determinante der erweiterten Matrix des Systems mit der Spalte der konstanten Glieder 0 sein.

Wir bestimmen die Determinante
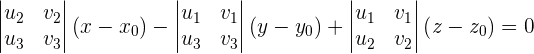
und weisen die Werte zu:

Wir setzen ein:
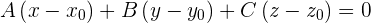
Wir lösen die Klammern auf

und mit der folgenden Gleichheit
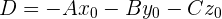
erhalten wir die allgemeine Form der Ebenengleichung:

Normalenvektor
Nun werden wir die Gleichung einer Ebene  mithilfe anderer Elemente aufstellen.
mithilfe anderer Elemente aufstellen.
Zunächst nehmen wir einen Vektor, der senkrecht zur Ebene ist und Normalenvektor 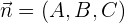 genannt wird. Außerdem nehmen wir einen festen Punkt auf der Ebene
genannt wird. Außerdem nehmen wir einen festen Punkt auf der Ebene 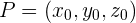
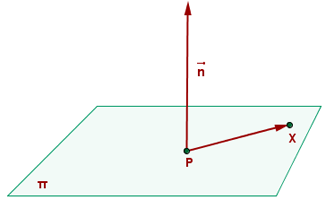
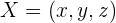 ist ein Punkt auf der Ebene.
ist ein Punkt auf der Ebene.
Wir bilden einen Vektor, der von 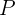 nach
nach  verläuft:
verläuft:

Solch ein Vektor steht senkrecht zu  , da er zu
, da er zu  gehört.
gehört.  steht senkrecht zu jedem Vektor der Ebene.
steht senkrecht zu jedem Vektor der Ebene.
Da die beiden Vektoren senkrecht zueinander stehen, ist ihr Skalarprodukt null:
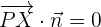
Auf diese Weise kann man die allgemeine Form der Ebenengleichung auch bestimmen, ausgehend von einem Punkt und einem Normalenvektor.
Ebenengleichung in Achsenabschnittsform
 ,
, 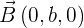 und
und  sind 3 Vektoren im Raum, durch den die Ebene
sind 3 Vektoren im Raum, durch den die Ebene  verläuft, und die sich auf den Bezugsachsen befinden.
verläuft, und die sich auf den Bezugsachsen befinden.
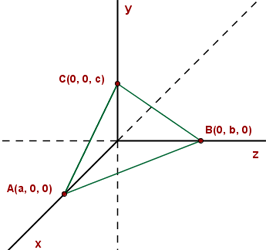
Wir bestimmen die Gleichung von  in ihrer Achsenabschnittsform ausgehend von ihrer allgemeinen Form.
in ihrer Achsenabschnittsform ausgehend von ihrer allgemeinen Form.
Wir nehmen an, dass wir die Gleichung der Ebene in ihrer allgemeinen Form  haben:
haben:

 ,
, 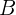 ,
, 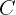 und
und  sind hierbei reelle Zahlen ungleich null.
sind hierbei reelle Zahlen ungleich null.
Wir subtrahieren  von beiden Seiten der Gleichung und dividieren im Anschluss beide Seiten durch
von beiden Seiten der Gleichung und dividieren im Anschluss beide Seiten durch  . Wir erhalten:
. Wir erhalten:
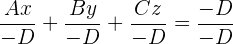
Wir formen die Brüche um:
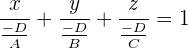
Die Nenner stimmen genau mit den Werten  ,
,  und
und  der anfangs genannten Vektoren im Raum überein:
der anfangs genannten Vektoren im Raum überein:

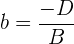
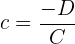
Somit haben wir bereits die Gleichung von  in ihrer Achsenabschnittsform:
in ihrer Achsenabschnittsform:

Denke daran, dass  ,
, 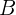 ,
, 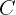 und
und  nicht null sein dürfen.
nicht null sein dürfen.
Aufgaben
1 Bestimme die Gleichungen der Ebene in Parameterform und in impliziter Form, die durch den Punkt  verläuft und die Richtungsvektoren
verläuft und die Richtungsvektoren  und
und 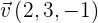 hat.
hat.
Da wir einen Punkt auf der Ebene und zwei Richtungsvektoren haben, setzen wir die Werte einfach in die Ebenengleichungen in Parameterform ein und erhalten:
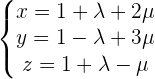
Um die Ebenengleichung in impliziter Form zu erhalten, schlagen wir folgende Gleichheit vor und lösen die Determinante:
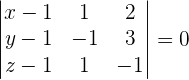
Wir erhalten die gesuchte Gleichung:

2Bestimme die Gleichungen der Ebene in Parameterform und in impliziter Form, die durch die Punkte 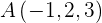 und
und 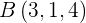 verläuft und den Vektor
verläuft und den Vektor  hat.
hat.
Zunächst betrachten wir den Punkt 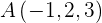 als Referenzpunkt auf der Ebene. Danach ermitteln wir ausgehend von
als Referenzpunkt auf der Ebene. Danach ermitteln wir ausgehend von  einen Vektor zum Punkt
einen Vektor zum Punkt 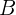 mithilfe von
mithilfe von 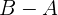 . Wir erhalten:
. Wir erhalten:

Dieser dient als der andere Richtungsvektor, sodass wir auf diese Weise alles in die Gleichungen der Ebene in ihrer Parameterform einsetzen können:
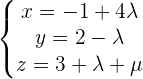
Nun können wir die Determinante bestimmen und erhalten so die allgemeine Form:
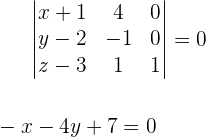
3Bestimme die Gleichungen der Ebene in Parameterform und in impliziter Form, die durch die Punkte 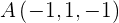 ,
,  und
und  verläuft
verläuft
Der Punkt  ist hierbei ein Referenzpunkt auf der Ebene. Davon ausgehend können wir 2 Richtungsvektoren anhand von
ist hierbei ein Referenzpunkt auf der Ebene. Davon ausgehend können wir 2 Richtungsvektoren anhand von 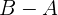 und
und 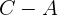 bestimmen:
bestimmen:
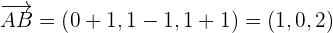
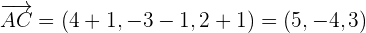
Unter Verwendung von  als Punkt der Ebene und der Richtungsvektoren können wir die Ebenengleichungen in Parameterform aufstellen:
als Punkt der Ebene und der Richtungsvektoren können wir die Ebenengleichungen in Parameterform aufstellen:

Damit können wir die folgende Determinante (gleich null) lösen und erhalten die Ebenengleichung in impliziter oder allgemeiner Form:

4Gegeben ist die Ebene 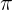 mit den Gleichungen in Parameterform:
mit den Gleichungen in Parameterform:
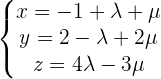
Überprüfe, ob die Punkte 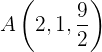 und
und 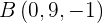 zur Ebene gehören.
zur Ebene gehören.
Zunächst bestimmen wir die Ebenengleichung anhand der folgenden Determinante:
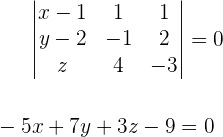
Da wir nun die Gleichung haben, setzen wir die Punkte  und
und 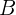 ein, um herauszufinden, ob die Punkte zur Ebene gehören oder nicht:
ein, um herauszufinden, ob die Punkte zur Ebene gehören oder nicht:
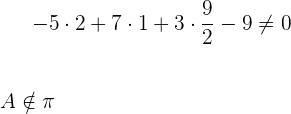

Da wir ein Ergebnis ungleich null erhalten, gehört keiner der Punkte zu der Ebene.
5Bestimme die Gleichung der Ebene in Achsenabschnittsform, die durch die Punkte 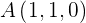 ,
, 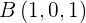 und
und  verläuft.
verläuft.
Wir nehmen den Punkt  als Referenzpunkt und ermitteln davon ausgehend zwei Vektoren, die jeweils nach
als Referenzpunkt und ermitteln davon ausgehend zwei Vektoren, die jeweils nach 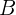 und
und 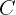 verlaufen und uns als Richtungsvektoren dienen:
verlaufen und uns als Richtungsvektoren dienen:
 .
.
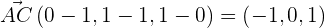 .
.
Mit dieser Information können wir anhand der Determinante die Ebenengleichung bestimmen:

Nun subtrahieren wir 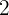 und dividieren beide Seiten durch
und dividieren beide Seiten durch 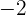 . So erhalten wir die Gleichung in Achsenabschnittsform:
. So erhalten wir die Gleichung in Achsenabschnittsform:
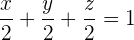 .
.
6Bestimme die Gleichung der Geraden  , die durch den Punkt
, die durch den Punkt 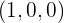 verläuft und senkrecht zur Ebene
verläuft und senkrecht zur Ebene  steht.
steht.
Da die Gerade senkrecht zur Ebene steht, ist der Normalenvektor der Ebene der Richtungsvektor der Geraden, die durch den Punkt 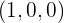 verläuft.
verläuft.
Den Normalenvektor der Ebene erhalten wir aus den Koeffizienten der Variablen, also  . Damit können wir die Geradengleichung wie folgt darstellen::
. Damit können wir die Geradengleichung wie folgt darstellen::
 .
.
7Bestimme die Gleichung der Ebene, die durch den Punkt  verläuft und die Gerade mit der folgenden Gleichung enthält:
verläuft und die Gerade mit der folgenden Gleichung enthält:
 .
.
Aus der Geradengleichung erhalten wir einen Punkt 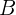 und den Vektor
und den Vektor  .
.
Den Punkt 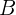 können wir ermitteln, indem wir jeden Nenner 0 setzen, sodass die Gleichheit immer erfüllt ist, also
können wir ermitteln, indem wir jeden Nenner 0 setzen, sodass die Gleichheit immer erfüllt ist, also  . Der Normalenvektor der Geraden ergibt sich aus den Nennern
. Der Normalenvektor der Geraden ergibt sich aus den Nennern 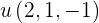 .
.
Nun bilden wir den Richtungsvektor mit 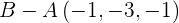 und können u als den anderen Richtungsvektor festlegen:
und können u als den anderen Richtungsvektor festlegen:
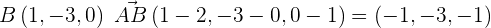 .
.
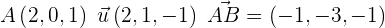 .
.
Das bedeutet, dass wir die Gleichung der Ebene mit dem bereits erwähnten Verfahren ermitteln können, was zu folgendem Ergebnis führt  .
.
Mit KI zusammenfassen:













