Kapitel
Es gibt mehrere Möglichkeiten, den Flächeninhalt eines Dreiecks zu bestimmen, je nachdem, welche Daten bekannt sind.
Grundseite und Höhe sind bekannt
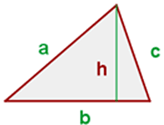
Wenn die Grundseite 
und die Höhe 
des Dreiecks bekannt sind, kann der Flächeninhalt durch das Produkt aus Grundseite und Höhe, geteilt durch 2, berechnet werden
Zwei Seitenlängen und der dazwischenliegende Winkel sind bekannt
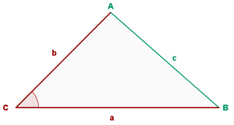
Sind zwei Seiten des Dreiecks und der Winkel zwischen ihnen bekannt, so ergibt sich die Formel zur Bestimmung des Flächeninhalts aus dem Produkt der beiden Seiten und dem Sinus des Winkels zwischen ihnen.
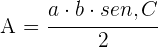
Kreisumfang eines Dreicks
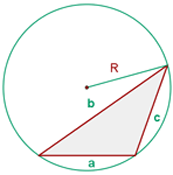
Wenn alle drei Seiten 
des Dreiecks und der Radius 
des Umkreises bekannt sind, ergibt sich die Formel für den Flächeninhalt aus dem Produkt der drei Seiten, geteilt durch den vierfachen Radius des Umkreises.
Inkreis eines Dreiecks
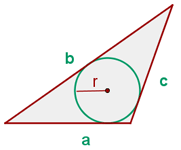
Wenn die drei Seiten des Dreiecks und der Radius 
des Inkreises bekannt sind, ergibt sich die Formel zur Bestimmung des Flächeninhalts aus dem Produkt aus dem Radius des Umfangs und dem halben Kreisumfang des Dreiecks
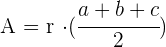
Der halbe Umfang wird in der Regel wie folgt berechnet
Die Formel für den Flächeninhalt lautet in der Regel
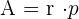
Satz des Heron
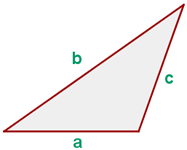
Wenn die drei Seiten des Dreiecks bekannt sind, lautet die Formel zur Bestimmung des Flächeninhalts wie folgt
.
ist hierbei der halbe Umfang des Dreiecks
.
Die Koordinaten der Eckpunkte sind bekannt
Wenn die Eckpunkte eines Dreiecks bekannt sind, gibt es zwei Möglichkeiten, den Flächeninhalt zu berechnen
Anhand der Vektoren
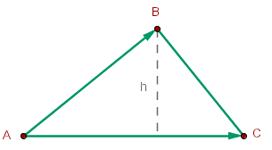
Wenn die Eckpunkte 
des Dreiecks bekannt sind, entspricht der Flächeninhalt der Hälfte des Skalarprodukts aus dem Vektor senkrecht auf 
und dem Vektor 
.
Beispiel: Berechne den Flächeninhalt eines Dreiecks mit den folgenden Eckpunkten: 
y 
.
1Als Erstes berechnen wir die Vektoren und
.
.
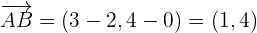2Wir berechnen den Vektor senkrecht zu
.
3Wir wenden die Formel zur Berechnung des Flächeninhalts des Dreiecks an
.
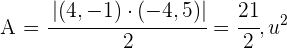Die Determinanten sind bekannt
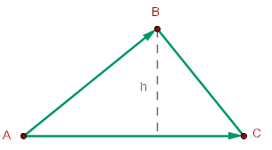
Wenn die Eckpunkte 
des Dreiecks bekannt sind, entspricht der Flächeninhalt der Hälfte des Absolutwerts der Determinante aus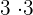 
, deren Zeilen aus den Eckpunkten bestehen und die in der dritten Spalte das Element eins enthalten
.
Zur Lösung wenden wir die Regel von Sarrus an.
Beispiel: Berechne den Flächeninhalt eines Dreicks mit den folgenden Eckpunkten: y .
1Als Erstes setzen wir die Eckpunkte in die Formel des Flächeninhalts ein
.
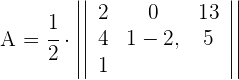2Wir wenden die Regel von Sarrus an, um die Determinante zu berechnen
.
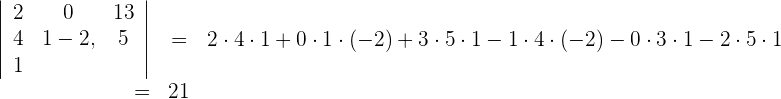3Der gesuchte Flächeninhalt ist also
.
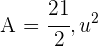Die Eckpunkte eines Dreiecks im Raum sind bekannt
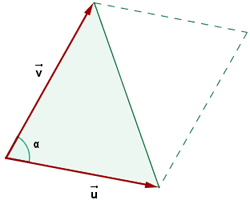
Wenn die Eckpunkte eines Dreiecks bekannt sind, entspricht der Flächeninhalt der Hälfte der halben Maßzahl des Vektorprodukts der Vektoren, die zwei seiner Seiten entsprechen
.
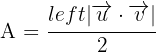Beispiel: Berechne den Flächeninhalt eines Dreiecks mit den folgenden Eckpunkten: 
und 
.
1Als Erstes berechnen wir die Vektoren der zwei Seiten
.
.
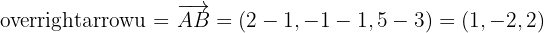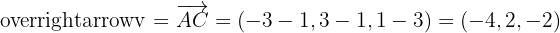2Wir berechnen das Vektorprodukt aus 
und 
.
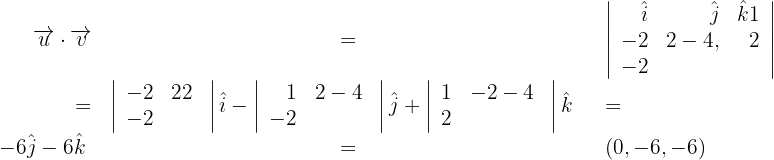3Wir berechnen die Größe von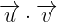 
.
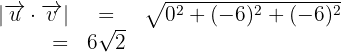4Unser gesuchter Flächeninhalt lautet also
.
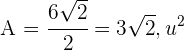Drei kollineare Punkte
Drei Punkte sind kollinear, wenn der Flächeninhalt des Dreiecks null ist.
Beispiel: Überprüfe, ob die Punkte 
und 
kollinear sind.
1Als Erstes setzen wir die Eckpunkte in die Formel für den Flächeninhalt ein
.
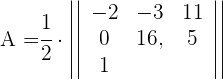2Um die Determinante zu berechnen, wenden wir die Regel von Sarrus an
.
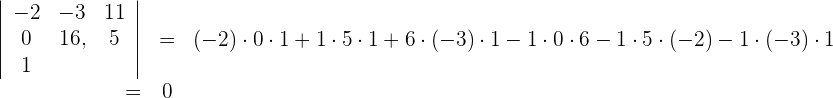3Somit ist unser gesuchter Flächeninhalt 
. Dies bedeutet, dass die Punkte kollinear sind.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
