
Definition eines geometrischen Ortes
Eine Menge von Punkten, die eine bestimmte Eigenschaft erfüllen, wird als geometrischer Ort bezeichnet.
Es ist üblich, dass die geometrische Eigenschaft, die den geometrischen Ort charakterisiert, auch in algebraischer Form dargestellt wird.
Beispiele für geometrische Orte
Mittelsenkrechte
Die Mittelsenkrechte eines Segments ist der geometrische Ort, an dem sich die Punkte der Ebene befinden, die von den Enden gleich weit entfernt sind. Grafisch gesehen ist die Mittelsenkrechte eine Gerade, die senkrecht auf einem Segment steht und es in zwei gleiche Teile teilt.
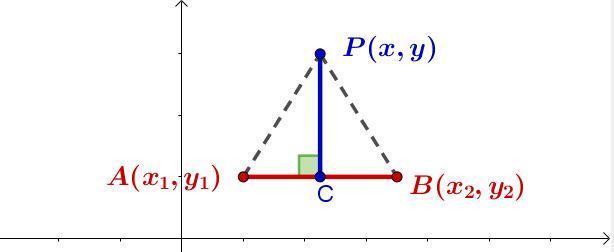
Wie in der Abbildung oben zu sehen ist, teilt CD das Segment AB in zwei gleiche Teile. Diese Beziehung kann algebraisch wie folgt ausgedrückt werden: 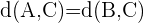
Somit haben wir zwei Dreiecke mit den gleichen Längen und somit auch die folgende Beziehung: 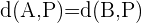
Im Allgemeinen ist jeder Punkt auf der Geraden, die von den Punkten P und C gebildet wird, gleich weit von den Punkten A bzw. B entfernt.
Unter Verwendung der Formel für die Entfernung in der kartesischen Ebene und unter Berücksichtigung der Tatsache, dass 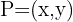 ,
,  und
und 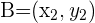 , kann diese Beziehung auch wie folgt geschrieben werden:
, kann diese Beziehung auch wie folgt geschrieben werden: 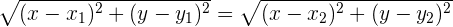
Beispiel
Finde die Gleichung der Winkelhalbierenden des Segments mit den Endpunkten A(2, 5) und B(4, -7).
Um die Gleichung der Winkelhalbierenden zu finden, verwenden wir die Gleichung (1), d. h. wir wissen, dass die Gerade Folgendes erfüllen muss
Wir setzen die gegebenen Werte ein und erhalten: 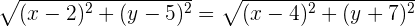
Wir quadrieren beide Seiten der Gleichung und erhalten im weiteren Verlauf: 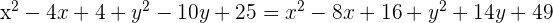
Wir streichen Terme und vereinfachen den Ausdruck: 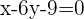
Das heißt, bei jedem Paar 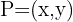 , das Gleichung (2) erfüllt, ist die Länge zwischen
, das Gleichung (2) erfüllt, ist die Länge zwischen 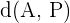 und
und 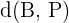 gleich (äquidistant).
gleich (äquidistant).
Winkelhalbierende
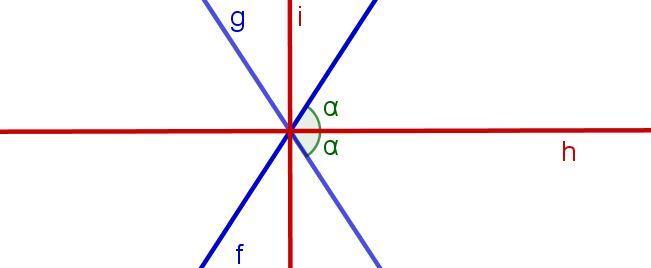
Die Winkelhalbierende eines Winkels ist der geometrische Ort der Punkte in der Ebene, die von den Geraden, die den Winkel bilden, gleich weit entfernt sind. Grafisch gesehen teilt eine Winkelhalbierende einen Winkel in zwei gleiche Teile. In der folgenden Abbildung ist zum Beispiel zu erkennen, dass die Geraden  und
und  zwei Winkelhalbierende haben: die Gerade
zwei Winkelhalbierende haben: die Gerade  und die Gerade
und die Gerade  , beide senkrecht zueinander.
, beide senkrecht zueinander.
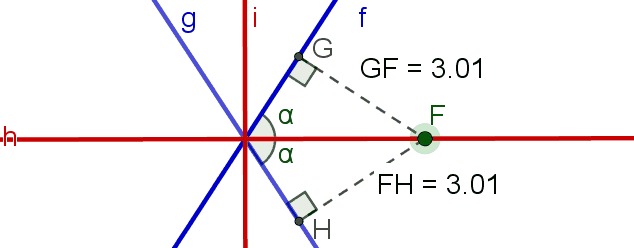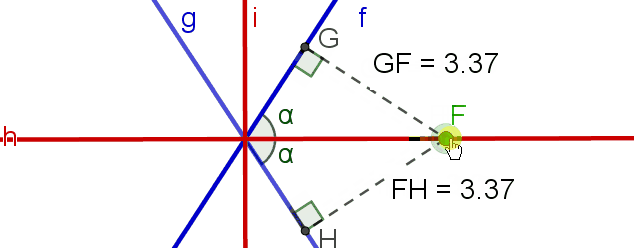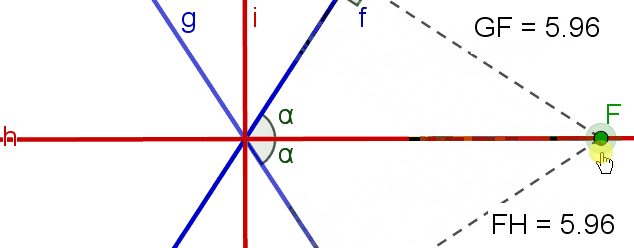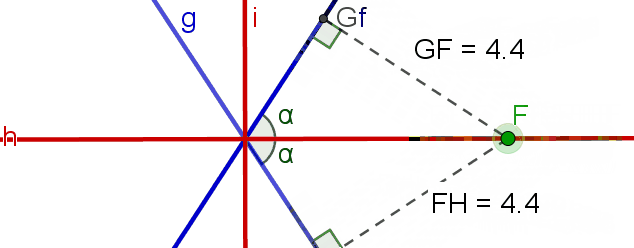
Wenn wir zum Beispiel ein Segment senkrecht zu den Geraden  und
und  zeichnen, das durch einen Punkt auf der Geraden
zeichnen, das durch einen Punkt auf der Geraden  verläuft, ist der Abstand gleich. Es genügt nämlich, dass der Winkel, den das Segment GF mit der Geraden f und das Segment FH mit der Geraden g bilden, den gleichen Winkel messen, damit der Abstand zu F gleich ist.
verläuft, ist der Abstand gleich. Es genügt nämlich, dass der Winkel, den das Segment GF mit der Geraden f und das Segment FH mit der Geraden g bilden, den gleichen Winkel messen, damit der Abstand zu F gleich ist.
Algebraisch betrachtet, erfüllt diese Beziehung Folgendes: 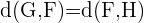
Wenn außerdem die Gerade  folgende Form hat:
folgende Form hat: 
und die Gerade  folgende Form hat:
folgende Form hat:  , gilt, dass
, gilt, dass 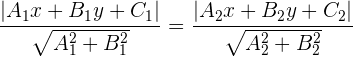
Beispiel 1
Finde die Gleichungen der Winkelhalbierenden der Winkel, die die Geraden  und
und  bestimmen.
bestimmen.
Wir nehmen Gleichung (3) und setzen ein 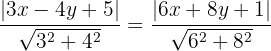
Wir berechnen und erhalten: 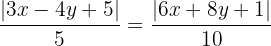
Das heißt 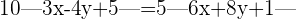
Da wir eine Gleichung mit Beträgen haben, gibt es zwei Fälle, für die die Gleichung erfüllt ist; der erste Fall ist 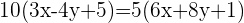
und der zweite Fall 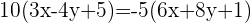
Um Gleichung (4) zu lösen, dividieren wir beide Seiten der Gleichung durch 5 und berechnen:

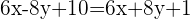
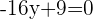
Um Gleichung (5) zu lösen, dividieren wir beide Seiten der Gleichung durch -5 und berechnen:
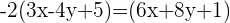
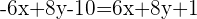
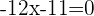
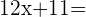
Somit sind die Gleichungen (5) und (6) die Winkelhalbierenden der Geraden  und
und 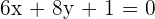 .
.
Beispiel 2
Berechne die Winkelhalbierenden der Winkel, die die Gerade 3x - 4y + 3 = 0 mit den Koordinatenachsen bildet
Dieses Problem hat zwei Aspekte: 1. Berechne die Winkelhalbierenden der Geraden 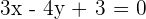 mit der Geraden
mit der Geraden  . 2. Berechne die Winkelhalbierenden der Geraden
. 2. Berechne die Winkelhalbierenden der Geraden 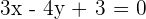 mit der Geraden
mit der Geraden  .
.
Um die Winkelhalbierenden der Geraden 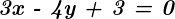 mit der Geraden
mit der Geraden 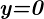 zu berechnen, setzen wir ein und verwenden Gleichung (5)
zu berechnen, setzen wir ein und verwenden Gleichung (5)
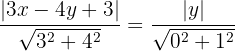
Wir berechnen und erhalten:
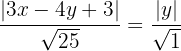
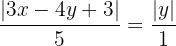
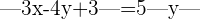
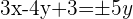
Wir berechnen die Gleichung der ersten Winkelhalbierenden:
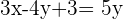
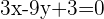
Wir berechnen die Gleichung der zweiten Winkelhalbierenden


Um die Winkelhalbierenden der Geraden 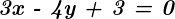 mit der Geraden
mit der Geraden 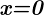 zu berechnen, setzen wir ein und verwenden Gleichung (5)
zu berechnen, setzen wir ein und verwenden Gleichung (5)
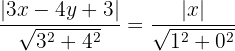
Wir berechnen und erhalten:
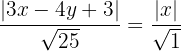
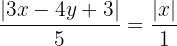
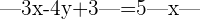
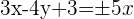
Wir berechnen die Gleichung der ersten Winkelhalbierenden:


Wir berechnen die Gleichung der zweiten Winkelhalbierenden
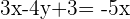
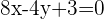
Mit KI zusammenfassen:













