Kapitel
In diesem Abschnitt werden wir uns das Konzept der Steigung einer Geraden ansehen sowie einige Möglichkeiten, die Steigung zu berechnen. Ausgehend vom Konzept der Steigung legen wir die Gleichung einer Geraden in "Punktsteigungsform" fest. Zum Abschluss sehen wir uns einige Beispiele dazu an, wie man die Gleichung einer Gerade in Punktsteigungsform erhält.

Steigung einer Geraden
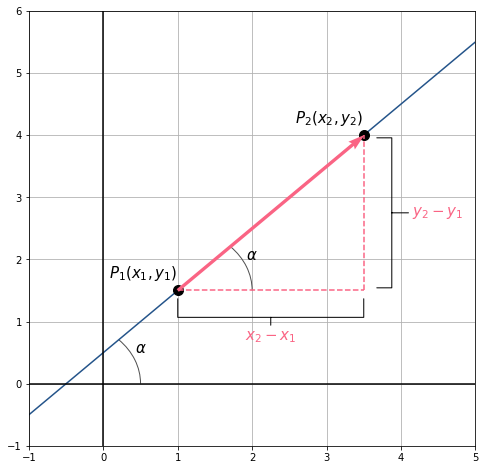
Wir sehen uns die Gerade in der folgenden Grafik an. Die Steigung der Geraden ist der Tanges des Winkels  , den die Gerade, die steigt, mit der
, den die Gerade, die steigt, mit der  -Achse bildet. Das heißt, wenn
-Achse bildet. Das heißt, wenn  der Winkel zwischen der Geraden und der
der Winkel zwischen der Geraden und der  -Achse ist, ist die Steigung
-Achse ist, ist die Steigung 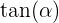 .
.
Die Steigung wird in der Regel  bezeichnet. Um die Steigung zu berechnen, gibt es folgende Möglichkeiten:
bezeichnet. Um die Steigung zu berechnen, gibt es folgende Möglichkeiten:
1 Mit dem Steigungswinkel
Wenn der Winkel  zwischen der Geraden und der
zwischen der Geraden und der  -Achse bekannt ist, wird die Steigung wie folgt berechnet:
-Achse bekannt ist, wird die Steigung wie folgt berechnet:
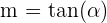
2 Mit dem Richtungsvektor der Geraden
Die Gerade kann mithilfe eines Richtungsvektors 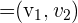 und eines Punktes
und eines Punktes 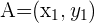 (der auf der Geraden liegt) definiert werden. Dies ist die Parameterform einer Geraden. In diesem Fall erhält man die Gerade wie folgt:
(der auf der Geraden liegt) definiert werden. Dies ist die Parameterform einer Geraden. In diesem Fall erhält man die Gerade wie folgt:
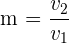
Wir stellen fest, dass die Steigung nicht von einem Punkt abhängt, sondern nur vom Richutngsvektor.
3 Mit zwei Punkten
Der Tanges des Winkel eines rechtwinkligen Dreiecks ist definiert als 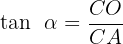 , wobei
, wobei  die Länge der Gegenkathete ist und
die Länge der Gegenkathete ist und 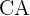 die Länge der Ankathete ist.
die Länge der Ankathete ist.
Wenn wir also die Grafik am Anfang betrachten, können wir sehen, dass 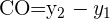 und
und 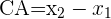 . Indem wir einsetzen, erhalten wir
. Indem wir einsetzen, erhalten wir
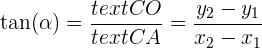
Die Steigung der Geraden, die durch die Punkte 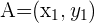 und
und 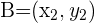 verläuft, wird also wie folgt berechnet:
verläuft, wird also wie folgt berechnet:
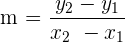
Interpretation der Steigung
Sehen wir uns folgende Grafik an. Der Winkel  befindet sich zwischen
befindet sich zwischen 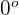 und
und 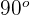 . Der Winkel ist somit ein spitzer Winkel.
. Der Winkel ist somit ein spitzer Winkel.
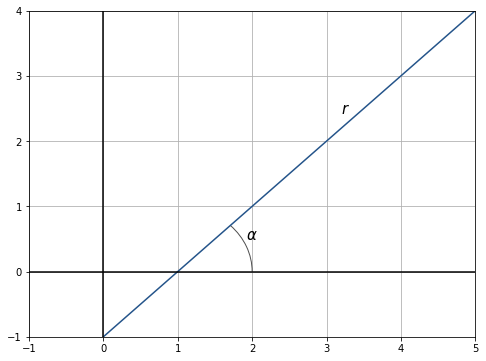
Wenn der Winkel, den die Gerade  mit dem positiven Abschnitt der
mit dem positiven Abschnitt der  -Achse bildet, ein spitzer Winkel ist, ist die Steigung also positiv und steigt mit zunehmendem Winkel - immer wenn der Winkel kleiner ist als
-Achse bildet, ein spitzer Winkel ist, ist die Steigung also positiv und steigt mit zunehmendem Winkel - immer wenn der Winkel kleiner ist als 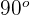 —. Somit misst die Steigung, "wie steil" die Gerade ist: Eine große Steigung bedeutet, dass die Gerade steil nach oben geneigt ist.
—. Somit misst die Steigung, "wie steil" die Gerade ist: Eine große Steigung bedeutet, dass die Gerade steil nach oben geneigt ist.
Nun sehen wir uns die folgende Grafik an. Der Winkel  ist größer als
ist größer als 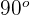 , jedoch kleiner als
, jedoch kleiner als 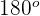 .
.
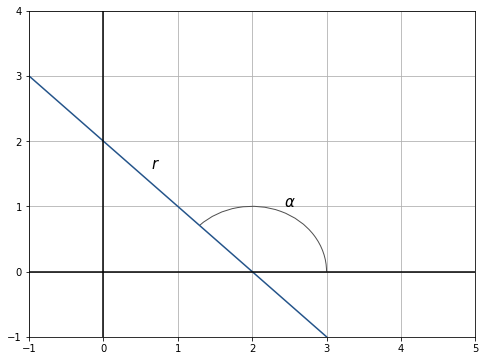
Wenn der Winkel, den die Gerade mit dem positiven Abschnitt der
-Achse bildet, stumpf ist - also größer als
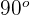 , jedoch kleiner als
, jedoch kleiner als 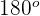 —, ist die Steigung negativ und geht gegen 0, wenn der Winkel größer wird. In ähnlicher Weise misst eine negative Steigung auch, wie steil die Gerade ist. In diesem Fall zeigt jedoch eine sehr große negative Steigung an, dass die Gerade sehr steil "nach unten" verläuft.
—, ist die Steigung negativ und geht gegen 0, wenn der Winkel größer wird. In ähnlicher Weise misst eine negative Steigung auch, wie steil die Gerade ist. In diesem Fall zeigt jedoch eine sehr große negative Steigung an, dass die Gerade sehr steil "nach unten" verläuft.
Geradengleichung in Punktsteigungsform
Nun möchten wir die Gleichung der Geraden in Punktsteigunsform erhalten. Wir können von verschiedenen Gleichungen ausgehen, beginnen aber mit der Normalform der Geradengleichung. 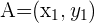 ist hierbei ein Punkt, der sich auf der Geraden befindet und
ist hierbei ein Punkt, der sich auf der Geraden befindet und 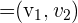 ist der Richtungsvektor.
ist der Richtungsvektor.
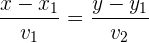
Wir multiplizieren beide Seiten mit 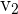 und erhalten
und erhalten
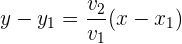
Schließlich, da

erhalten wir:
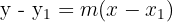
Dies ist die Geradengleichung in Punktsteigungsform.
Anmerkung: Um die Geradengleichung in Punktsteigungsform zu berechnen, benötigen wir einfach nur einen Punkt 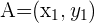 und die Steigung
und die Steigung  (diese lässt sich mittels irgendeiner der am Anfang dargestellten Möglichkeiten berechnen).
(diese lässt sich mittels irgendeiner der am Anfang dargestellten Möglichkeiten berechnen).
Beispiele
1 Wir haben eine Gerade, die durch den Punkt  verläuft und den Richtungsvektor
verläuft und den Richtungsvektor 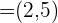 hat. Erstelle die Gleichung der Geraden in Punktsteigungsform.
hat. Erstelle die Gleichung der Geraden in Punktsteigungsform.
Lösung: Da wir einen Richtungsvektor  haben, ist die Steigung gegeben durch
haben, ist die Steigung gegeben durch
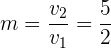
Wir setzen also  und
und 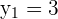 in die Punktsteigungsgleichung ein und erhalten
in die Punktsteigungsgleichung ein und erhalten

Hier müssen wir allerding die Vorzeichen beachten, da:  .
.
2 Bestimme die Geradengleichung in Punktsteigungsform einer Geraden, die durch die Punkte  und
und 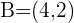 verläuft.
verläuft.
Lösung: Diesmal haben wir zwei Punkte, die auf der Geraden liegen, sodass die Steigung wie folgt berechnet wird:
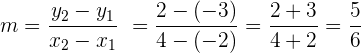
Indem wir also in die Gleichung in Punktsteigungsform einsetzen, erhalten wir

3 Bestimme die Geradengleichung in Punktsteigungsform einer Geraden, die durch den Punkt  verläuft und deren Neigung
verläuft und deren Neigung 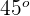 beträgt
beträgt
Lösung: Schließlich erhalten wir den Winkel zwischen der Geraden und der  -Achse. Die Steigung ist also gegeben durch
-Achse. Die Steigung ist also gegeben durch
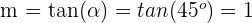
Die Geradengleichung in Punktsteigungsform lautet also:
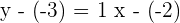
Das heißt
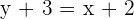
Mit KI zusammenfassen:













