
Ermittle die Geradengleichung
Ermittle die Gleichung der Geraden, die den Punkt 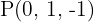 enthält und die parallel zur Geraden in Parameterform verläuft, die wie folgt gegeben ist
enthält und die parallel zur Geraden in Parameterform verläuft, die wie folgt gegeben ist
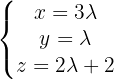
Aus der Parametrisierung ergibt sich, dass ein Richtungsvektor 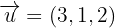 ist.
ist.
Da sie den Punkt 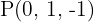 enthält, lautet die Geradengleichung
enthält, lautet die Geradengleichung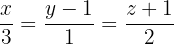
Ermittle die Gleichung der Geraden, die durch den Punkt  verläuft und parallel zu den Ebenen
verläuft und parallel zu den Ebenen 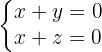 ist.
ist.
Wir berechnen die Normalenvektoren
 und
und 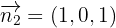
Der Richtungsvektor der Geraden muss senkrecht zu diesen stehen, so dass wir ihr Kreuzprodukt berechnen

Und da wir einen Richtungsvektor 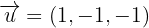 und einen Punkt P(2, 0, 0) haben, durch den die Gerade verläuft, lautet die Gleichung
und einen Punkt P(2, 0, 0) haben, durch den die Gerade verläuft, lautet die Gleichung

Ermittle die Gleichung in Parameterform der Geraden, die durch den Punkt 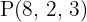 verläuft und die Richtung des Vektors
verläuft und die Richtung des Vektors  aufweist.
aufweist.
Ausgehend von einem Punkt, durch den die Gerade verläuft, und dem Richtungsvektor erhält man direkt die Geradengleichung in Parameterform
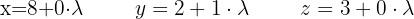
Wir vereinfachen und erhalten:
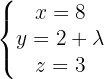
Ermittle die Gleichung der Geraden, die durch den Punkt  und parallel zu den folgenden Ebenen verläuft:
und parallel zu den folgenden Ebenen verläuft:
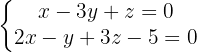
Wir berechnen die Normalenvektoren
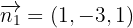 und
und 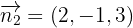
Der Richtungsvektor der Geraden muss senkrecht zu diesen stehen, so dass wir ihr Kreuzprodukt berechnen

Und da wir einen Richtungsvektor  und einen Punkt P(2, -1, 5) haben, durch den die Gerade verläuft, lautet die Gleichung
und einen Punkt P(2, -1, 5) haben, durch den die Gerade verläuft, lautet die Gleichung
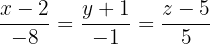
Ermittle die implizite Gleichung der Geraden, die durch den Punkt 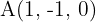 verläuft und die folgenden Geraden schneidet:
verläuft und die folgenden Geraden schneidet:

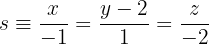
Um die Gleichung der Geraden zu erhalten, muss man feststellen, dass sie der Schnittpunkt der beiden Ebenen ist, die durch  gehen und die Geraden
gehen und die Geraden  und
und  enthalten.
enthalten.
1 Wir berechnen die Gleichung der Ebene, die  und
und  enthält. Ein Vektor dieser Ebene ist dann der Richtungsvektor der Geraden
enthält. Ein Vektor dieser Ebene ist dann der Richtungsvektor der Geraden  . Wir lösen
. Wir lösen  und erhalten:
und erhalten: 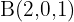 ist ein Punkt auf
ist ein Punkt auf  . Der andere Vektor ist also gegeben durch:
. Der andere Vektor ist also gegeben durch:

Ein Punkt auf der Ebene ist:  Die Vektoren sind:
Die Vektoren sind: 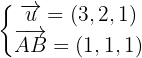 Daher ist die Gleichung der Ebene durch die folgende Determinante gegeben
Daher ist die Gleichung der Ebene durch die folgende Determinante gegeben
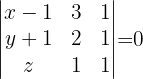
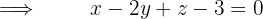
2 Wir erhalten die Gleichung der Ebene, die  und
und  enthält. Ein Vektor, der diese Ebene erzeugt, ist der Richtungsvektor der Geraden
enthält. Ein Vektor, der diese Ebene erzeugt, ist der Richtungsvektor der Geraden  . Wir lösen
. Wir lösen 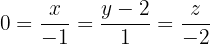 und erhalten:
und erhalten:  ist ein Punkt auf
ist ein Punkt auf  . Somit ist der andere erzeugende Vektor gegeben durch
. Somit ist der andere erzeugende Vektor gegeben durch

Ein Punkt auf der Ebene ist:  Die erzeugenden Vektoren sind:
Die erzeugenden Vektoren sind: 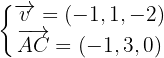 Daher ist die Gleichung der Ebene durch die folgende Determinante gegeben
Daher ist die Gleichung der Ebene durch die folgende Determinante gegeben

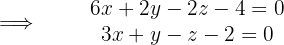
3 Wir erhalten die implizite Gleichung der Geraden. Wir nutzen die Gleichungen der zuvor erhaltenen Ebenen:
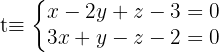
Ermittle die Punkte auf der Geraden
Gegeben sind die Punkte 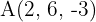 und
und  . Bestimme die Punkte der Geraden
. Bestimme die Punkte der Geraden  , bei denen mindestens eine Koordinate 0 ist.
, bei denen mindestens eine Koordinate 0 ist.
1 Wir berechnen die Gleichung der Geraden  . Da
. Da  Punkte auf der Geraden bekannt sind, berechnen wir die Differenz, um einen Richtungsvektor zu erhalten
Punkte auf der Geraden bekannt sind, berechnen wir die Differenz, um einen Richtungsvektor zu erhalten

 ) lautet die Gleichung in Parameterform
) lautet die Gleichung in Parameterform 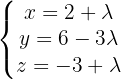
- Wenn die erste Koordinate 0 ist:
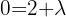 somit
somit 

- Wenn die zweite Koordinate 0 ist:
 somit
somit 
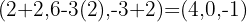
- Wenn die dritte Koordinate 0 ist:
 somit
somit 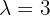
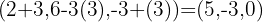 . Schließlich konnten wir
. Schließlich konnten wir  Punkte finden, bei denen mindestens eine der Koordinaten 0 war:
Punkte finden, bei denen mindestens eine der Koordinaten 0 war:  und
und  .
.Finde die Koordinaten des gemeinsamen Punktes der Ebene 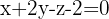 und der Geraden, die durch den Punkt
und der Geraden, die durch den Punkt 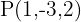 und den Vektor
und den Vektor  bestimmt wird
bestimmt wird
1 Wir ermitteln die Gleichung der beschriebenen Geraden
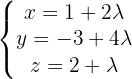


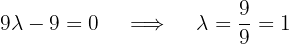

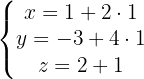

Mit KI zusammenfassen:












