
Definition einer Geraden
Eine Gerade  auf der Ebene ist durch einen beliebigen Punkt
auf der Ebene ist durch einen beliebigen Punkt  und eine vorgegebene Richtung
und eine vorgegebene Richtung  definiert.
definiert.
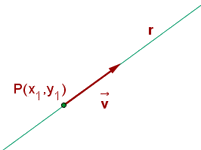
Vektorschreibweise der Geradengleichung
Wenn  ein Punkt der Geraden
ein Punkt der Geraden  ist, besitzt der Vektor
ist, besitzt der Vektor 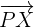 dieselbe Richtung wie der Vektor
dieselbe Richtung wie der Vektor  und ist gleich dem Skalrprodukt von
und ist gleich dem Skalrprodukt von  und
und 
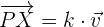
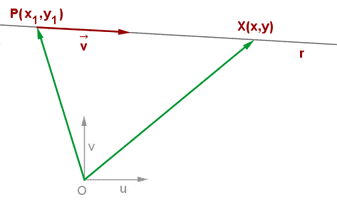
Bildet man die Differenz der Vektoren 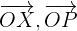 , erhält man
, erhält man
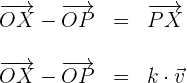
Durch Auflösen nach 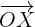 erhält man die Vektorgleichung der Geraden
erhält man die Vektorgleichung der Geraden

Beispiel: Eine Gerade verläuft durch den Punkt  und besitzt den Richtungsvektor
und besitzt den Richtungsvektor 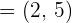 . Stelle die Vektorgleichung der Geraden auf.
. Stelle die Vektorgleichung der Geraden auf.
Setze den Punkt und den Richtungsvektor in die allgemeine Form der Geradengleichung in Vektorschreibweise ein
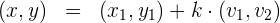
und du erhältst
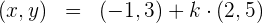
Parameterform der Geradengleichung
Auf Basis der Vektorgleichung der Geraden erhält man durch Umformen:

Durch Gleichsetzen erhält man die Parameterform der Geradengleichung.
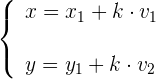
Beispiel: Eine Gerade verläuft durch den Punkt  und besitzt den Richtungsvektor
und besitzt den Richtungsvektor 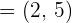 . Stelle ihre Gleichungen in Parameterform auf.
. Stelle ihre Gleichungen in Parameterform auf.
Setze den Punkt und den Richtungsvektor in die allgemeine Form der Geradengleichung in Vektorschreibweise ein
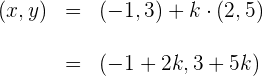
und du erhältst die Gleichungen in Parameterschreibweise
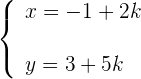
Hauptform der Geraden
Durch Eliminieren des Parameters  aus den Parametergleichungen und anschließendes Gleichsetzen erhält man die Hauptform der Geradengleichung.
aus den Parametergleichungen und anschließendes Gleichsetzen erhält man die Hauptform der Geradengleichung.
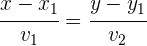
Beispiel: Eine Gerade verläuft durch den Punkt  und besitzt den Richtungsvektor
und besitzt den Richtungsvektor 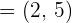 . Stelle die Geradengleichung in der Hauptform auf.
. Stelle die Geradengleichung in der Hauptform auf.
Setze den Punkt und den Richtungsvektor in die Hauptform der Geradengleichung ein

Punkt-Steigungsform der Geradengleichung
Löse ausgehend von der Hauptform der Geradengleichung die Nenner auf und vereinfache:
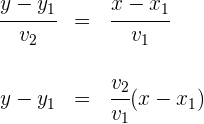
Mit 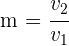 als Steigung
als Steigung
erhält man:
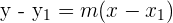
Beispiel: Stelle die Gleichung der Geraden auf, die durch die Punkte  und
und 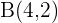 verläuft.
verläuft.
Berechne die Steigung
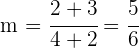
Setze den Wert in die Punkt-Steigungsform der Geraden ein und du erhältst
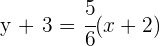
Allgemeine Geradengleichung
Basierend auf der Hauptform der Geraden
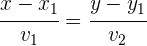
Eliminiere die Nenner:
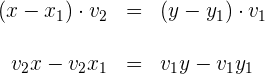
Bringe alle Terme auf die linke Seite:
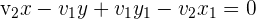
Wandle um:
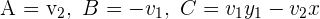
Du erhältst die allgemeine Geradengleichung.
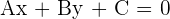
Die Komponenten des Richtungsvektors sind:
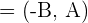
Die Steigung der Geraden ist:

Beispiel: Stelle die Gleichung der Geraden auf, die durch den Punkt 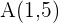 verläuft und deren Steigung
verläuft und deren Steigung 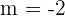 ist.
ist.
Wende die Punkt-Steigungsform an und du erhältst
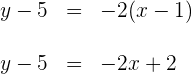
Bringe alle Terme auf die linke Seite:
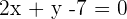
Explizite Form der Geraden
Wenn die allgemeine Geradenform nach  aufgelöst wird, erhält man die explizite Geradengleichung :
aufgelöst wird, erhält man die explizite Geradengleichung :
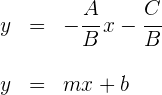
Der Koeffizient von  ist die Steigung
ist die Steigung  .
.
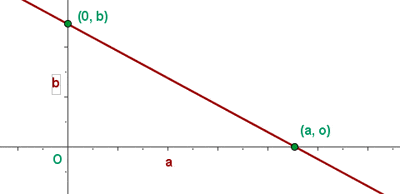
Das konstante Glied  wird als Ordinatenabschnitt (auch: Abschnitt auf der y-Achse) der Geraden bezeichnet, dessen Punkt
wird als Ordinatenabschnitt (auch: Abschnitt auf der y-Achse) der Geraden bezeichnet, dessen Punkt  der Achsenabschnittspunkt ist.
der Achsenabschnittspunkt ist.
Beispiel: Stelle die explizite Gleichung einer Geraden auf, die durch den Punkt 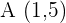 verläuft und die Steigung
verläuft und die Steigung  aufweist.
aufweist.
Ermittle die Gerade anhand der Punkt-Steigungs-Form
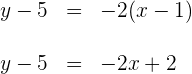
Löse nach  auf
auf
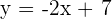
Kanonische (bzw. symmetrische) Geradengleichung
Wenn eine Gerade durch die Punkte 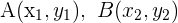 definiert ist, ist der Richtungsvektor
definiert ist, ist der Richtungsvektor
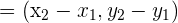
Durch Einsetzen dieser Werte in die Hauptform der Geraden erhält man die Gleichung für die Gerade, die durch zwei Punkte verläuft
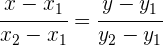
Bringe alle Terme auf die linke Seite:
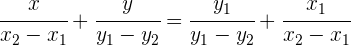
Du erhältst
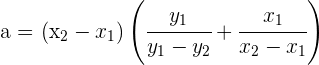

die kanonische Geradengleichung
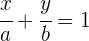
Beispiel: Stelle die kanonische Geradengleichung der Geraden auf, die durch 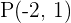 verläuft und deren Richtungsvektor
verläuft und deren Richtungsvektor  ist.
ist.
Stelle die Hauptform der Geradengleichung auf

Schreibe in die allgemeine Form der Geradengleichung um
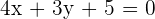
Teile beide Seiten durch  un du erhältst
un du erhältst
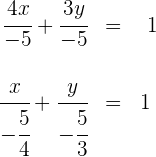
Gemischte Aufgaben
Stelle die Gleichung der Geraden in Vektorschreibweise auf, die durch die Punkte  und
und 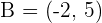 verläuft. Stelle die Vektorgleichung der Geraden auf.
verläuft. Stelle die Vektorgleichung der Geraden auf.
1 Der Richtungsvektor ist kollinear zum Vektor

2 Setze einen der Punkte und den Richtungsvektor in die Geradengleichung in Vektorschreibweise ein
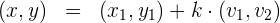
und du erhältst

Stelle die Gleichung der Geraden in Parameterform auf, die durch die Punkte  und
und 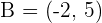 verläuft. Stelle die Vektorgleichung der Geraden auf.
verläuft. Stelle die Vektorgleichung der Geraden auf.
1 Der Richtungsvektor ist kollinear zum Vektor

2 Setze einen der Punkte und den Richtungsvektor in die Geradengleichung in Parameterform ein
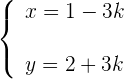
Stelle die Hauptform der Geraden auf, die durch die Punkte  und
und 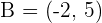 verläuft. Stelle die Vektorgleichung der Geraden auf.
verläuft. Stelle die Vektorgleichung der Geraden auf.
1 Der Richtungsvektor ist kollinear zum Vektor

2 Setze einen der Punkte und den Richtungsvektor in die Hauptform der Geradengleichung ein
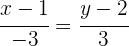
Stelle die Gleichung der Geraden auf, die durch  verläuft und einen Steigungswinkel von
verläuft und einen Steigungswinkel von  aufweist.
aufweist.
1 Die Steigung der Geraden ist gleich dem Tangens des Steigungswinkels:
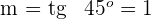
2 Durch Einsetzen in die Punkt-Steigungsform der Geraden erhältst du
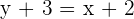
Stelle die allgemeine Geradengleichung der Geraden auf, die durch die Punkte  und
und 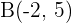 verläuft.
verläuft.
1 Berechne den Richtungsvektor:

2 Berechne den Wert von 
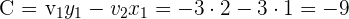
3 Durch Einsetzen in die allgemeine Geradengleichung erhältst du
Mit KI zusammenfassen:













