Berechne den Abstand des Punkts  zur Geraden
zur Geraden  der Gleichung
der Gleichung 
Um den Abstand einer Geraden  mit der allgemeinen Gleichung
mit der allgemeinen Gleichung  zu einem Punkt
zu einem Punkt  zu berechnen, kann folgende Formel verwendet werden:
zu berechnen, kann folgende Formel verwendet werden:  In diesem Fall ergeben sich für die Koeffizienten und Koordinaten des Punktes folgende Werte:
In diesem Fall ergeben sich für die Koeffizienten und Koordinaten des Punktes folgende Werte: 




Durch Einsetzen der Variablen in die vorherige Formel erhält man  Der Abstand zwischen
Der Abstand zwischen  und
und  ist also gleich
ist also gleich 
Berechne den Abstand zwischen  und
und 
Für die vorgegebenen Geraden  und
und  gilt nur eine der folgenden Optionen: entweder sind sie parallel oder sie haben einen Punkt gemeinsam. Wenn sie parallel sind, können sie nebeneinander oder auch aufeinander liegen, also dieselbe Gerade beschreiben. Aufgrund dieser möglichen Optionen ist es wichtig, vor der Berechnung des Abstands der Geraden ihre Steigung zu berechnenm, um wissen, um welche der Optionen es sich handelt. Es handelt sich um parallele Geraden, wenn sie dieselbe Steigung haben. Andernfalls haben sie einen Schnittpunkt. Die Steigung einer Geraden in ihrer allgemeinen Form
gilt nur eine der folgenden Optionen: entweder sind sie parallel oder sie haben einen Punkt gemeinsam. Wenn sie parallel sind, können sie nebeneinander oder auch aufeinander liegen, also dieselbe Gerade beschreiben. Aufgrund dieser möglichen Optionen ist es wichtig, vor der Berechnung des Abstands der Geraden ihre Steigung zu berechnenm, um wissen, um welche der Optionen es sich handelt. Es handelt sich um parallele Geraden, wenn sie dieselbe Steigung haben. Andernfalls haben sie einen Schnittpunkt. Die Steigung einer Geraden in ihrer allgemeinen Form  wird am Term
wird am Term  erichtlich. Die Geraden
erichtlich. Die Geraden  und
und  haben also die Steigungen
haben also die Steigungen  und
und  Da beide Geraden dieselbe Steigung haben, können wir also schlussfolgern, dass sie parallel zueinander sind. Diese Lagebeziehung kann auch als
Da beide Geraden dieselbe Steigung haben, können wir also schlussfolgern, dass sie parallel zueinander sind. Diese Lagebeziehung kann auch als  dargestellt werden.Da
dargestellt werden.Da  , müssen wir nun herausfinden, ob die Geraden deckungsgleich sind oder nebeneinander verlaufen. Dafür genügt es, einen Punkt auf
, müssen wir nun herausfinden, ob die Geraden deckungsgleich sind oder nebeneinander verlaufen. Dafür genügt es, einen Punkt auf  zu finden, der nicht auf
zu finden, der nicht auf  liegt. Um das zu ermitteln, setzen wir in der Geradengleichung von
liegt. Um das zu ermitteln, setzen wir in der Geradengleichung von 
 und erhalten
und erhalten  ; das bedeutet, dass
; das bedeutet, dass  ein Punkt auf der Geraden
ein Punkt auf der Geraden  ist, aber kein Punkt auf der Geraden
ist, aber kein Punkt auf der Geraden  , da
, da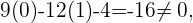 Für diesen Wert geht die Gleichung von
Für diesen Wert geht die Gleichung von  nicht auf. Wir können also schlussfolgern, dass
nicht auf. Wir können also schlussfolgern, dass  und
und  parallele Geraden sind, die nicht aufeinanderliegen. Jetzt wählen wir einen beliebigen Punkt
parallele Geraden sind, die nicht aufeinanderliegen. Jetzt wählen wir einen beliebigen Punkt  auf einer der beiden Geraden und berechnen den Abstand von diesem Punkt zur anderen Geraden. Wir nehmen den Punkt
auf einer der beiden Geraden und berechnen den Abstand von diesem Punkt zur anderen Geraden. Wir nehmen den Punkt  , da wir bereits wissen, dass er
, da wir bereits wissen, dass er  erfüllt. Wir verwenden die Formel
erfüllt. Wir verwenden die Formel und erhalten
und erhalten
Eine Gerade verläuft parallel zur Geraden mit der Gleichung  und liegt
und liegt  Einheiten vom Koordinatenurpsrung entfernt. Wie lautet ihre Gleichung?
Einheiten vom Koordinatenurpsrung entfernt. Wie lautet ihre Gleichung?
Wir benennen die gesuchte Gerade mit  . Wie wir wissen, sind zwei Geraden dann parallel, wenn ihre Koeffizienten von
. Wie wir wissen, sind zwei Geraden dann parallel, wenn ihre Koeffizienten von  und
und  entsprechend proportional sind. Damit
entsprechend proportional sind. Damit  müssen die Koeffizienten proportional sein, das heißt, die Gleichung, die die Gerade
müssen die Koeffizienten proportional sein, das heißt, die Gleichung, die die Gerade  beschreibt, muss die Form
beschreibt, muss die Form  haben.
haben.
Wir wissen auch, dass man den Abstand von einem Punkt  zu einer Geraden
zu einer Geraden  anhand der folgenden Formel ermitteln kann:
anhand der folgenden Formel ermitteln kann:

Wenn der Punkt  im Koordinatenursprung liegt, wird die Formel reduziert:
im Koordinatenursprung liegt, wird die Formel reduziert:

D.h.für  muss gelten:
muss gelten:

Wir prüfen, ob es tatsächlich Geraden gibt, die den Abstand  vom Ursprung haben und parallel zueinander sind:
vom Ursprung haben und parallel zueinander sind:

Die Gleichungen der beiden Geraden lauten daher:  .
.
Gegeben ist ein Viereck  mit den Scheitelpunkten
mit den Scheitelpunkten  und
und 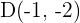 . Berechne seine Fläche.
. Berechne seine Fläche.
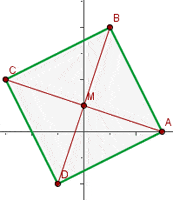
Die gesuchte Fläche erhalten wir, indem wir die Längen von  und
und  miteinander multiplizieren. Wir beginnen also mit der Berechnung der Seitenlängen.
miteinander multiplizieren. Wir beginnen also mit der Berechnung der Seitenlängen.


Durch Multiplizieren der Werte erhalten wir:


Die Fläche des Vierecks beträgt also 20.
Berechne den Winkel, der zwischen den Geraden  und
und  liegt, wenn ihre Richtungsvektoren
liegt, wenn ihre Richtungsvektoren  und
und 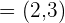 sind.
sind.
Wenn  und
und  nicht Null sind, ist der Winkel, der zwischen ihnen liegt die einzige reelle Zahl
nicht Null sind, ist der Winkel, der zwischen ihnen liegt die einzige reelle Zahl  , für die gilt:
, für die gilt:  wobei
wobei  und
und 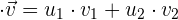 .Wir rechnen weiter und erhalten
.Wir rechnen weiter und erhalten 

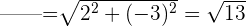 Daher ist
Daher ist  und folglich
und folglich 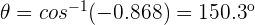
Berechne den Winkel, der zwischen den Geraden  und
und  liegt.
liegt.
Um den Winkel zu berechnen, kannst du folgende Formel verwenden:

wobei  und
und  die Steigungen der Geraden
die Steigungen der Geraden  und
und  sind.
sind.
Wenn die Geradengleichung in die Form  gebracht wurde, wird die Steigung durch den Koeffizienten, der bei
gebracht wurde, wird die Steigung durch den Koeffizienten, der bei  steht angezeigt, das heißt durch
steht angezeigt, das heißt durch  . Wir stellen
. Wir stellen  und
und  wie folgt dar:
wie folgt dar:
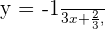

und erhalten die Steigungen  und
und 
Durch Einsetzen der Steigungen erhalten wir:


Das heißt, 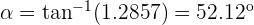 .
.
Finde eine parallele und eine orthogonale Gerade zu  , die beide durch den Punkt
, die beide durch den Punkt  verlaufen.
verlaufen.
Wie wir wissen, sind zwei Geraden dann parallel, wenn sie dieselbe Steigung haben. Um eine parallele Gerade zu  zu finden, müssen wir erst ihre Steigung kennen.
zu finden, müssen wir erst ihre Steigung kennen.
Die Gleichung von  kann umgeschrieben werden:
kann umgeschrieben werden:

In diesem Ausdruck ist die Steigung leicht ersichtlich, da sie durch den Koeffizient, der bei  steht, angezeigt wird, d.h. die Steigung ist
steht, angezeigt wird, d.h. die Steigung ist  .
.
Wir nennen die gesuchte parallele Gerade  und ihre Steigung
und ihre Steigung  . Wir haben herausgefunden, dass
. Wir haben herausgefunden, dass 
wobei  die Steigung von
die Steigung von  ist.
ist.
Für die Koordinaten von  , durch den die parallele Gerade verläuft, können wir die Punkt-Steigungs-Formel verwenden:
, durch den die parallele Gerade verläuft, können wir die Punkt-Steigungs-Formel verwenden:  .
.
Durch Einsetzen der bekannten Werte erhalten wir:


Wir können schlussfolgern, dass  und
und  .
.
Um eine orthogonale Gerade zu  zu finden, gehen wir ähnlich vor, aber mit einer anderen Bedingung bei der Steigung. Wir benennen die gesuchte orthogonale Gerade mit
zu finden, gehen wir ähnlich vor, aber mit einer anderen Bedingung bei der Steigung. Wir benennen die gesuchte orthogonale Gerade mit  . In diesem Fall muss für die Steigung
. In diesem Fall muss für die Steigung  gelten, dass
gelten, dass  , um die Orthogonalität zu gewährleisten. Daher ist
, um die Orthogonalität zu gewährleisten. Daher ist  , also
, also  .
.
Wir verwenden erneut die Punkt-Steigungs-Formel und die Koordinaten des Punktes  und erhalten
und erhalten
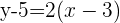
 hat also die Gleichung
hat also die Gleichung  , wobei
, wobei  .
.
Ermittle die Gleichung der Mittelsenkrechte des Segments mit den Endpunkten  und
und  .
.
Als Mittelsenkrechte eines Segments bezeichnet man den geometrischen Ort der Punkte der Ebene, die von den Enden gleich weit entfernt sind. Mathematisch gesehen, sind das die Punkte  , für welche die Gleichung
, für welche die Gleichung 
für die Endpunkte  und
und  aufgeht. Es ist zu beachten, dass
aufgeht. Es ist zu beachten, dass und
und 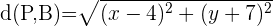 Um die gesuchte Gleichung zu finden, setzen wir die beiden Gleichungen gleich und vereinfachen den Ausdruck:
Um die gesuchte Gleichung zu finden, setzen wir die beiden Gleichungen gleich und vereinfachen den Ausdruck:
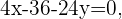 Vereinfache weiter, indem du mit
Vereinfache weiter, indem du mit  multiplizierst:
multiplizierst:
Finde die Gleichung der Winkelhalbierenden der Winkel, die zwischen den Geraden  und
und  liegen.
liegen.
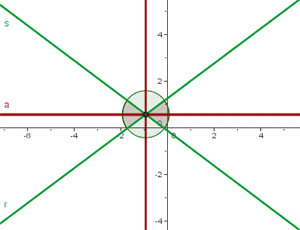
Bei zwei sich schneidenden Geraden ist die Winkelhalbierende des Winkels, der zwischen ihnen liegt, der geometrische Ort auf der Ebene, der von beiden gleich weit entfernt ist. Wir suchen also die Gleichung der Punkte  , für die gilt:
, für die gilt:

Die Formel für den Abstand von einem Punkt  zu einer Geraden
zu einer Geraden  ist durch folgende Formel definiert:
ist durch folgende Formel definiert:

Aus der vorherigen Formel ergibt sich:

und

Durch Gleichsetzen von  erhalten wir
erhalten wir

Wir multiplizieren mit  und erhalten
und erhalten

Wir erhalten also zwei Gleichungen:
 und
und 
Jede beschreibt die Gleichung der zugehörigen Winkelhalbierenden.
Für die erste Gleichung erhalten wir

Für die zweite Gleichung erhalten wir

Ermittle die Gleichung der Geraden, die orthogonal zu  ist und durch den Punkt
ist und durch den Punkt  verläuft.
verläuft.
Wir erkennen, dass die Steigung der Geraden 
 ist, da man die Steigung bei einer Gleichung mit der Form
ist, da man die Steigung bei einer Gleichung mit der Form  am Koeffizienten von
am Koeffizienten von  ablesen kann.
ablesen kann.
Wir bezeichnen die gesuchte Gerade mit  . Ihre Steigung
. Ihre Steigung  sein, da das Produkt aus ihrer Steigung und der Steigung der Geraden
sein, da das Produkt aus ihrer Steigung und der Steigung der Geraden  gleich -1 sein muss, damit die Orthogonalität gegeben ist.
gleich -1 sein muss, damit die Orthogonalität gegeben ist.
Die Koordinaten von  können wir nun in die Punkt-Steigungs-Formel
können wir nun in die Punkt-Steigungs-Formel  einsetzen.
einsetzen.
Die gesuchte Gleichung ist daher:

oder auch
Finde die Gleichung der Winkelhalbierenden der Winkel, die zwischen den Geraden 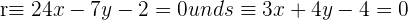 liegen.
liegen.
Bei zwei sich schneidenden Geraden ist die Winkelhalbierende des Winkels, der zwischen ihnen liegt, der geometrische Ort auf der Ebene, der von beiden gleich weit entfernt ist. Wir suchen also die Gleichung, für deren Punkte  gilt:
gilt:  .
.
Daher ist

und

Durch Gleichsetzen von  erhalten wir
erhalten wir

Wir multiplizieren mit  und erhalten
und erhalten

Wir erhalten also zwei Gleichungen:
 und
und 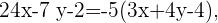 . Jede der beiden beschreibt die Gleichung einer der Winkelhalbierenden.
. Jede der beiden beschreibt die Gleichung einer der Winkelhalbierenden.
Für die erste Gleichung erhalten wir

Für die zweite Gleichung erhalten wir

Welcher Winkel liegt zwischen den Geraden mit den Gleichungen
a

b


s_2 \equiv \displaystyle\frac{x+4}{\sqr{3}}=\frac{y-1}{-1} [/latex
a
Da die Geradengleichungen in Parameterform vorliegen, können wir ihre Richtungsvektoren anhand der Koeffizienten von  ablesen. Das heißt
ablesen. Das heißt  ist der Richtungsvektor von
ist der Richtungsvektor von  und
und  ist der Richtungsvektor von
ist der Richtungsvektor von  .
.
Wir verwenden nun die Formel zur Berechnung von Winkeln zwischen Vektoren

um den gesuchten Winkel zu erhalten.
Wir setzen die Koordinaten von  ein:
ein:


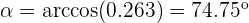
b
Die Richtungsvektoren dieser Geraden sind  und
und  .
.
Der Winkel, der zwischen ihnen liegt, ist wie folgt definiert:


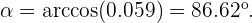
Welcher Winkel liegt zwischen den Geraden mit den Gleichungen:
a

b

a
Zuerst müssen wir den Richtungsvektor jeder der Geraden ermitteln, um dann den Winkel dazwischen berechnen zu können. Gesucht ist der Winkel zwischen  und
und  .
.
Der Richtungsvektor einer Geraden  ist
ist  . Für
. Für  und
und  haben wir also die Richtungsvektoren
haben wir also die Richtungsvektoren  und
und 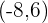 .
.
Der Winkel zwischen den beiden Vektoren berechnet sich wie folgt:

Durch Einsetzen der Vektoren erhalten wir



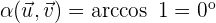
b
In diesem Fall sind die Richtungsvektoren der Geradne  und
und  gleich
gleich  und
und  .
.
Wir sehen, dass

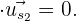
Das heißt, dass der Winkel zwischen  und
und  90º beträgt, da die Bedingung
90º beträgt, da die Bedingung 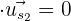 gleich
gleich  ist.
ist.
Gegeben sind die Geraden  und
und  . Berechne die Steigung
. Berechne die Steigung  so, dass zwischen den Geraden ein Winkel von 45° liegt.
so, dass zwischen den Geraden ein Winkel von 45° liegt.
Die Richtungsvektoren von  und
und  seien
seien  und
und  . Gesucht wird
. Gesucht wird  , sodass
, sodass 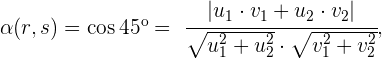 Die vorherige Formel hilft uns dabei, den Winkel zwischen den beiden Geraden zu berechnen. Wir setzen die Koordinaten der Richtungsvektoren und den Winkel
Die vorherige Formel hilft uns dabei, den Winkel zwischen den beiden Geraden zu berechnen. Wir setzen die Koordinaten der Richtungsvektoren und den Winkel 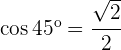 ein und erhalten:
ein und erhalten: Wir quadrieren die gesamte Gleichung:
Wir quadrieren die gesamte Gleichung:

 Nun multiplizieren wir die Gleichung mit
Nun multiplizieren wir die Gleichung mit 


 Mithilfe der allgemeinen Formel für quadratische Gleichungen können wir die vorherige Gleichung lösen:
Mithilfe der allgemeinen Formel für quadratische Gleichungen können wir die vorherige Gleichung lösen:
 ist der Koeffizient des quadratischen Terms,
ist der Koeffizient des quadratischen Terms,  der Koeffizient des linearen Terms und
der Koeffizient des linearen Terms und  das konstante Glied. In unserem Fall sind sie durch folgende Werte gegeben:
das konstante Glied. In unserem Fall sind sie durch folgende Werte gegeben:

Mit der allgemeinen Formel erhalten wir also





Die möglichen Lösungen für die Steigung, mit denen die gesuchten Bedingungen erfüllt werden, sind  und
und 
Eine Gerade ist orthogonal zur Geraden mit der Gleichung  und liegt
und liegt  Einheiten vom Ursprung entfernt. Wie lautet ihre Gleichung?
Einheiten vom Ursprung entfernt. Wie lautet ihre Gleichung?
Für jede beliebige Gleichung  in ihrer kanonischen Form
in ihrer kanonischen Form

sind die Koordinaten des Richtungsvektors  .
.
Außerdem wissen wir, dass zwei Geraden  orthogonal sind, wenn ihre Richtungsvektoren
orthogonal sind, wenn ihre Richtungsvektoren  es ebenso sind, bzw. wenn
es ebenso sind, bzw. wenn

wobei 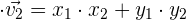 . In unserem Fall ist der Richtungsvektor von
. In unserem Fall ist der Richtungsvektor von  gleich
gleich  .
.
Wir nennen die gesuchte Gerade  . Der Richtungsvektor von
. Der Richtungsvektor von  hat die Koordinaten
hat die Koordinaten  , daher ist
, daher ist  .
.
Wir wissen außerdem, dass der Abstand von einem Punkt  zu einer Geraden
zu einer Geraden  durch folgende Formel ermittelt werden kann:
durch folgende Formel ermittelt werden kann:
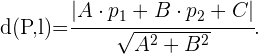
Wenn der Punkt  im Koordinatenursprung liegt, wird die Formel reduziert:
im Koordinatenursprung liegt, wird die Formel reduziert:
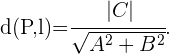
D.h.für  muss gelten:
muss gelten:

Wir prüfen, ob es tatsächlich Geraden gibt, die den Abstand  vom Ursprung haben und parallel zueinander sind:
vom Ursprung haben und parallel zueinander sind:

Die Gleichungen der beiden Geraden lauten daher:  .
.
Gegeben ist das Dreieck  ; Berechne die Gleichungen der Höhen und bestimme den Höhenschnittpunkt des Dreiecks.
; Berechne die Gleichungen der Höhen und bestimme den Höhenschnittpunkt des Dreiecks.
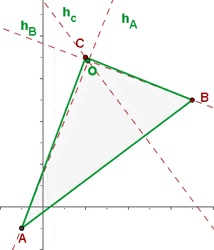
Zuerst ermitteln wir die Gleichungen der Höhen des Dreiecks. Wir benennen die Gleichungen der drei Geraden mit  und
und  . Sie verlaufen entsprechend durch die Punkte
. Sie verlaufen entsprechend durch die Punkte  und
und  .
.
Für  ist
ist  , dass heißt, die Steigung
, dass heißt, die Steigung  des Segments
des Segments  multipliziert mit der Steigung
multipliziert mit der Steigung  von
von  muss als Lösung
muss als Lösung  ergeben.
ergeben.
Da wir die Koordinaten der Punkte  und
und  kennen, können wir die Steigung mit der Formel
kennen, können wir die Steigung mit der Formel  berechnen.
berechnen.
 und
und
Mit den Koordinaten von  ,
,  und der Punkt-Steigungs-Formel können wir die Geradengleichung für
und der Punkt-Steigungs-Formel können wir die Geradengleichung für  aufstellen.
aufstellen.  ist also die Gleichung, die
ist also die Gleichung, die definiert.
definiert.
Durch Vereinfachen erhalten wir  .
.
Auf dieselbe Art können wir die anderen Gleichungen aufstellen.
Wir beginnen mit den Steigungen.


Dann nehmen wir die Punkt-Steigungs-Formel für 


und für 


Um die Koordinaten des Höhenschnittpunkts zu finden, genügt es, den Schnittpunkt von zwei der Höhenlinien zu ermitteln.
Wir lösen das lineare Gleichungssystem auf:

Der Höhenschnittpunkt liegt bei 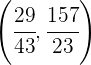 .
.
Eine Gerade mit der Gleichung  ist die Mittelsenkrechte des Segments
ist die Mittelsenkrechte des Segments  mit Endpunkt
mit Endpunkt  und den Koordinaten
und den Koordinaten  . Bestimme die Koordinaten des anderen Endpunkts.
. Bestimme die Koordinaten des anderen Endpunkts.
Die Gleichung, die die Gerade beschreibt, auf der das Segment  und der Punkt
und der Punkt  liegen, nennen wir
liegen, nennen wir  .
.
Da die Gerade  die Mittelsenkrechte des Segments
die Mittelsenkrechte des Segments  sein muss, muss
sein muss, muss  gelten, das heißt,
gelten, das heißt,  , wobei
, wobei  und
und  die entsprechenden Steigungen von
die entsprechenden Steigungen von  und
und  sind.
sind.
Aus der vorherigen Analyse ergibt sich  , denn aus
, denn aus  in der Form
in der Form  erhalten wir
erhalten wir  .
.
Mithilfe der Punkt-Steigungs-Formel ermitteln wir die Gleichung, die die Gerade beschreibt, die durch den Punkt  verläuft und die Steigung
verläuft und die Steigung  hat. Wir vereinfachen den Ausdruck zu
hat. Wir vereinfachen den Ausdruck zu  und erhalten
und erhalten  .
.
Jetzt sehen wir, dass  , der Schnittpunkt von
, der Schnittpunkt von  und
und  , für die Gleichungen von
, für die Gleichungen von  und
und  aufgehen muss. Um die Koordinaten von
aufgehen muss. Um die Koordinaten von  zu finden, genügt es daher, das lineare Gleichungssystem aufzulösen:
zu finden, genügt es daher, das lineare Gleichungssystem aufzulösen:

Wir lösen das LGS und erhalten die Koordinaten des Punktes  ;
;  .
.  ist außerdem der Mittelpunkt des Segments
ist außerdem der Mittelpunkt des Segments  , was mathematisch bedeutet, dass
, was mathematisch bedeutet, dass 
wobei  die Koordinaten von
die Koordinaten von  sind.
sind.
Wir setzen Koordinate für Koordinate gleich und erhalten

Durch Einsetzen der bereits bekannten Werte von  und
und  erhalten wir
erhalten wir
Folglich ist

Der Endpunkt  hat daher die Koordinaten
hat daher die Koordinaten  .
.
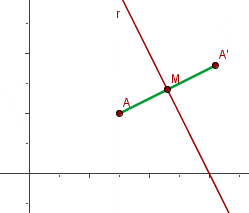
Finde den Symmetriepunkt  des Punktes
des Punktes  der Geraden
der Geraden 
Wir nennen die gesuchte Gleichung  . Sie beschreibt die Gerade, auf der das Segment
. Sie beschreibt die Gerade, auf der das Segment  und der Punkt
und der Punkt  liegen. Unserer Vermutung nach muss
liegen. Unserer Vermutung nach muss  erfüllt sein, das heißt
erfüllt sein, das heißt  .
.  und
und  sind dabei die entsprechenden Steigungen der Geraden
sind dabei die entsprechenden Steigungen der Geraden  und
und  .
.
Die Gleichung von  in ihrer expliziten Form ist
in ihrer expliziten Form ist  . Die Steigung von
. Die Steigung von  ist daher einfach der Koeffizient von x, das heißt
ist daher einfach der Koeffizient von x, das heißt  . Daraus lässt sich schließen, dass
. Daraus lässt sich schließen, dass  .
.
Mithilfe der Punkt-Steigungs-Formel ermitteln wir die Gleichung, die die Gerade beschreibt, die durch den Punkt  verläuft und die Steigung
verläuft und die Steigung  hat. Wir vereinfachen den Ausdruck
hat. Wir vereinfachen den Ausdruck  und erhalten
und erhalten  .
.
Jetzt erkennen wird, dass  , der Schnittpunkt von
, der Schnittpunkt von  und
und  , beide Gleichungen erfüllen muss: die der Geraden
, beide Gleichungen erfüllen muss: die der Geraden  und die von
und die von  . Um die Koordinaten von
. Um die Koordinaten von  zu finden, genügt es daher, das lineare Gleichungssystem aufzulösen:
zu finden, genügt es daher, das lineare Gleichungssystem aufzulösen:

Wir lösen das LGS und erhaltendie Koordinaten des Punktes  :
: 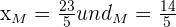 .
.  ist der Mittelpunkt des Segments
ist der Mittelpunkt des Segments  und kann mathematisch so ausgedrückt werden:
und kann mathematisch so ausgedrückt werden:

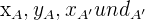 sind dabei die Koordinaten von
sind dabei die Koordinaten von  .
.
Wir setzen Koordinate für Koordinate gleich und erhalten

Durch Einsetzen der bereits bekannten Werte von  und
und  erhalten wir
erhalten wir

Folglich ist
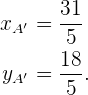
Der Symmetriepunkt  hat also die Koordinaten
hat also die Koordinaten 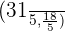 .
.
Mit KI zusammenfassen:



