Kapitel
Punkt-Richtungsform der Geradengleichung
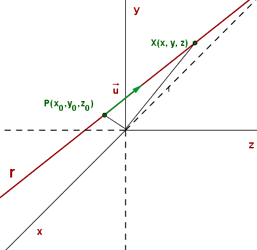
Eine Gerade 
wird als Zusammenschluss aneinandergereihter Punkte im Raum mit einem Punkt 
und einer Richtung 
definiert.
Wenn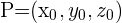 
ein Punkt auf der Geraden ist und ihr Richtungsvektor, besitzt der Vektor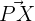 
, der vom Punkt zu einem anderen Punkt 
auf der Geraden verläuft, dieselbe Richtung wie , d.h. er ist gleich multipliziert mit einem Skalar:
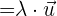
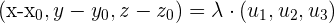
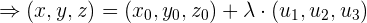
Parameterform der Geradengleichung
Auf Basis der Punkt-Richtungsform der Geraden erhalten wir durch Umformen die Gleichung:
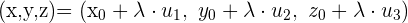
Diese entspricht der Parameterform der Geradengleichung:
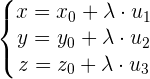
Hauptform (oder explizite Form) der Geradengleichung
Durch Auflösen nach λ und Angleichen von λ in der Parameterform, erhalten wir die Hauptform der Geradengleichung:
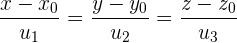
Allgemeine (oder implizite) Form der Geradengleichung
Eine Gerade wird durch den Schnittpunkt zweier Ebenen definiert.
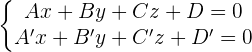
Auf Basis der Hauptform der Geradengleichung erhalten wir
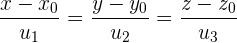
Wir betrachten eine der beiden Gleichungen, zum Beispiel
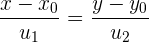
Wir entfernen die Nenner
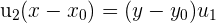
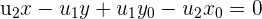
und erhalten folgendes Ergebnis:
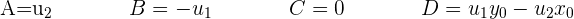
Wir erhalten die Gleichung einer der beiden Ebenen:
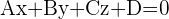
Wir fahren mit den anderen beiden Gleichungen ähnlich fort, zum Beispiel:
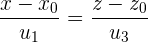
Und erhalten die Gleichung der zweiten Ebene 
.
Geradengleichungen: gemischte Aufgaben
Ermittle die explizite und implizite Form der Geradengleichung der Gerade, die durch den Punkt A = (1, 2, 1) verläuft und den Richtungsvektor 
besitzt.
1 Parametergleichungen
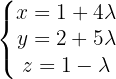
2 Gleichung in expliziter Form
Wir nehmen die Gleichung in Parameterform und lösen nach 
auf:
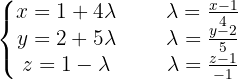
Wir erhalten die Hauptform der Geradengleichung, indem wir die vorherigen Terme gleichsetzen:
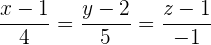
3 Gleichung in impliziter Form
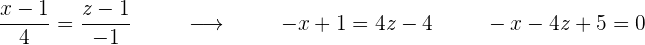
Die implizite (oder allgemeine) Form der Geradengleichung ist:
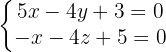
Ermittle die explizite und implizite Form der Geradengleichung der Gerade, die durch die Punkte A(1, 0, 1) und B(0, 1, 1) verläuft.
1 Finde einen Richtungsvektor
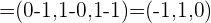
2 Gleichung in Parameterform
3 Explizite Form der Geradengleichung
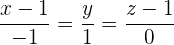
4 Implizite Form der Geradengleichung
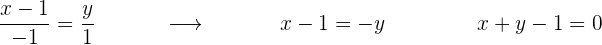
Die implizite (oder allgemeine) Form der Geradengleichung ist:
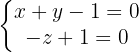
3 r sei die Gerade der Gleichung:
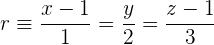
Liegen die Punkte A(0, −2, −2) und B(3, 2, 6) auf r?
1 Punkt A
Wir setzen die Koordinaten von A in alle Teile der Gleichung ein: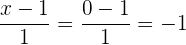
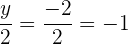
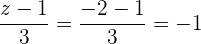
Durch Einsetzen von A geht die Gleichung auf
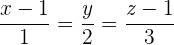
Daher gilt
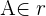
2 Punkt B
Wir setzen die Koordinaten von B in alle Teile der Gleichung ein:
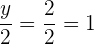
Durch Einsetzen von B geht die Gleichung nicht auf
Daher gilt
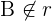
Gegeben ist die Gerade r:
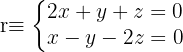
Stelle die Gleichung der Geraden in Hauptform und Parameterform auf.
1 Bringe eine der Variablen auf die andere Seite der Gleichung
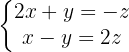
2 Verwende die Cramersche Regel, um 
und 
in Abhängigkeit von 
zu erhalten
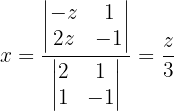
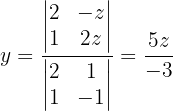
3 Indem wir zwei Werte zuordnen, erhalten wir zwei Punkte auf der Geraden
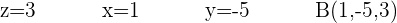
4 Wir erhalten einen Richtungsvektor
Die Geradengleichung in Parameterform lautet daher:
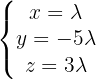
Die Geradengleichung in Hauptform lautet:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
