
Die Geradengleichung in Parameterform
Du kennst sicherlich schon die Geradengleichung der Form:

Wobei:
 : ist die Steigung der Geraden
: ist die Steigung der Geraden
 : ist der Schnittpunkt mit der '
: ist der Schnittpunkt mit der ' '-Achse
'-Achse
Allerdings kann eine Gerade auch in Form eines Gleichungssystem dargestellt werden:

Jede Gleichung enthält jeweils die Werte aller Punkte der Geraden für  und
und  .
.
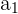 und
und  sind die Koordinaten des Punktes
sind die Koordinaten des Punktes 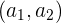 , durch den die Gerade verläuft.
, durch den die Gerade verläuft.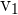 und
und 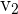 sind die Koordinaten eines Richtungsvektors
sind die Koordinaten eines Richtungsvektors 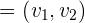 , der uns die Richtung der Geraden vorgibt
, der uns die Richtung der Geraden vorgibt ist eine reelle Zahl, die es uns ermöglicht, jede Koordinate der Geraden entsprechend dem ihr zugewiesenen Wert zu bestimmen.
ist eine reelle Zahl, die es uns ermöglicht, jede Koordinate der Geraden entsprechend dem ihr zugewiesenen Wert zu bestimmen.
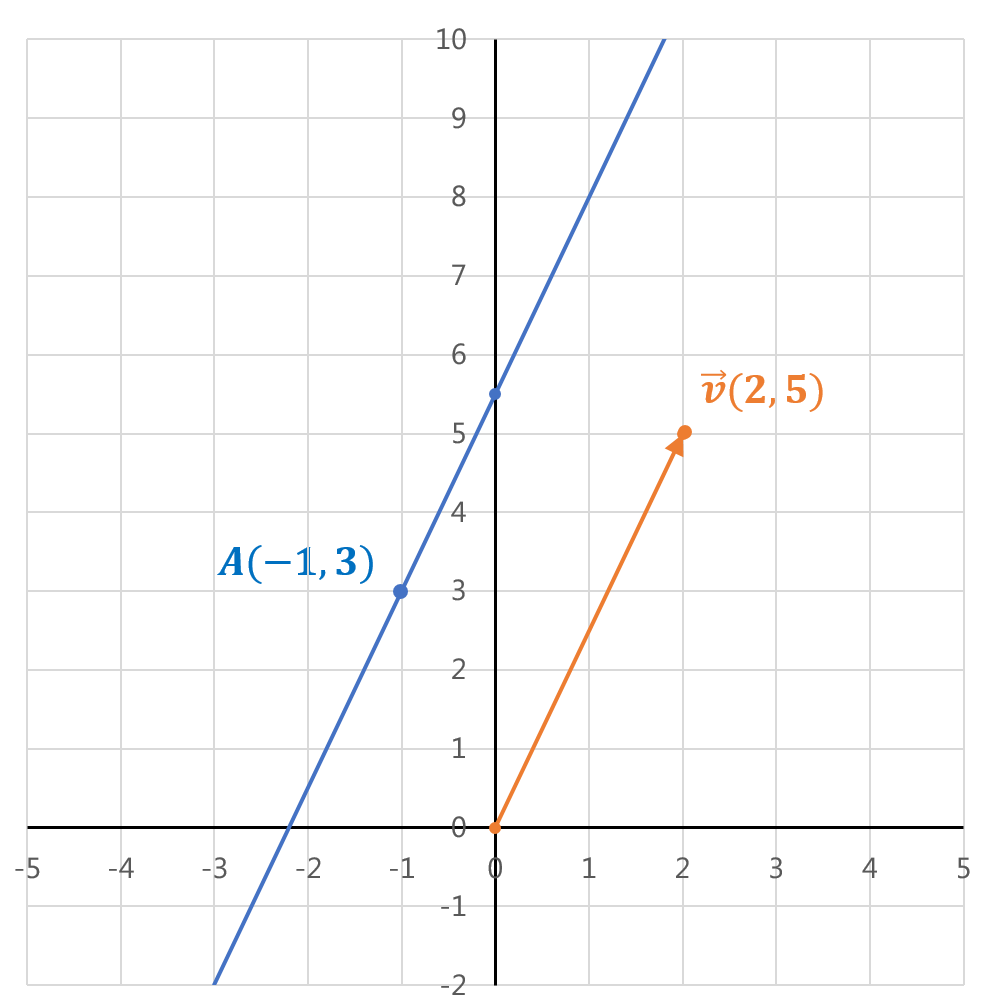
Sieh dir folgende Abbilung an:
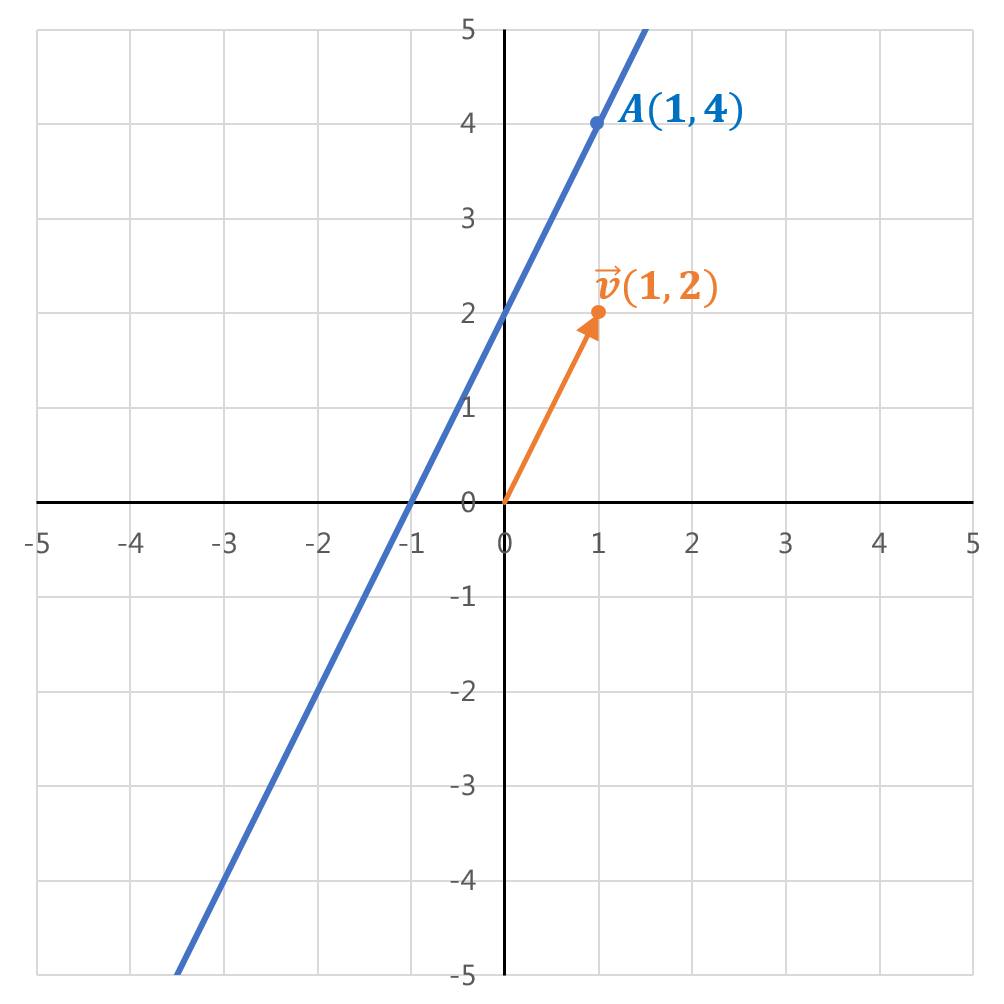
Wie du sehen kannst, verläuft die Gerade ' ' durch den Punkt
' durch den Punkt 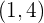 und die Koordinaten des Richtungsvektors sind
und die Koordinaten des Richtungsvektors sind 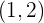 .
.
Der Richtungsvektor ist immer parallel zur Geraden ' '
'
Die Gleichung der Geraden ' ' kann wie folgt geschrieben werden:
' kann wie folgt geschrieben werden:
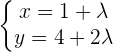
Beispiel für die Gleichung in Parameterform
Eine Gerade verläuft durch den Punkt  und hat den Richtungsvektor
und hat den Richtungsvektor 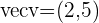 . Schreibe ihre Gleichungen in Parameterform.
. Schreibe ihre Gleichungen in Parameterform.
Wir wissen, dass  y
y 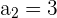
und  y
y 
somit:
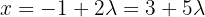
Grafisch dargestellt:
Mit KI zusammenfassen:













