Eine Gerade verläuft durch den Punkt  und hat den Richtungsvektor
und hat den Richtungsvektor 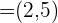 .
.
Stelle die zugehörige Geradengleichung in Punkt-Richtungsform auf.
Eine Gerade verläuft durch den Punkt  und hat den Richtungsvektor
und hat den Richtungsvektor 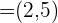 . Stelle die zugehörige Geradengleichung in Punkt-Richtungsform auf:
. Stelle die zugehörige Geradengleichung in Punkt-Richtungsform auf: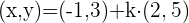
Eine Gerade verläuft durch den Punkt  und hat den Richtungsvektor
und hat den Richtungsvektor 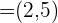 .
.
Stelle die zugehörigen Geradengleichungen in Parameterform auf.
Eine Gerade verläuft durch den Punkt  und hat den Richtungsvektor
und hat den Richtungsvektor 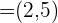 . Stelle die zugehörigen Geradengleichungen in Parameterform auf:
. Stelle die zugehörigen Geradengleichungen in Parameterform auf:
Eine Gerade verläuft durch den Punkt  und hat den Richtungsvektor
und hat den Richtungsvektor 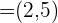 .
.
Stelle die zugehörige Hauptform der Geradengleichung auf.
Eine Gerade verläuft durch den Punkt  und hat den Richtungsvektor
und hat den Richtungsvektor 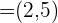 . Stelle die zugehörige Hauptform der Geradengleichung auf:
. Stelle die zugehörige Hauptform der Geradengleichung auf: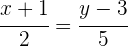
Stelle die jeweilge Geradengleichung in Punkt-Steigungs-Form auf:
a Eine Gerade verläuft durch den Punkt  und hat den Richtungsvektor
und hat den Richtungsvektor 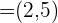 .
.
b Eine Gerade verläuft durch die Punkte  und
und  .
.
c Eine Gerade verläuft durch  und hat eine Steigung von
und hat eine Steigung von 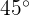 .
.
Stelle die jeweilige Geradengleichung in Punkt-Steigungs-Form auf:
a Eine Gerade verläuft durch den Punkt  und hat den Richtungsvektor
und hat den Richtungsvektor 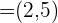 .
.

b Eine Gerade verläuft durch die Punkte  und
und 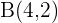 .
.
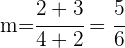
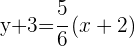
c Eine Gerade verläuft durch den Punkt  und hat eine Steigung von
und hat eine Steigung von 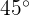 .
.

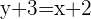
Stelle die jeweilige allgemeine Geradengleichung der Geraden auf:
a Eine Gerade verläuft durch den Punkt  und hat den Richtungsvektor
und hat den Richtungsvektor  gleich
gleich  .
.
b Eine Gerade verläuft durch den Punkt  und hat die Steigung
und hat die Steigung  .
.
Stelle die jeweilige allgemeine Geradengleichung der Geraden auf:
a Eine Gerade verläuft durch den Punkt  und hat den Richtungsvektor
und hat den Richtungsvektor  gleich
gleich  .
.

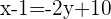
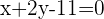
b Eine Gerade verläuft durch den Punkt 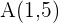 und hat die Steigung
und hat die Steigung  .
.
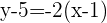
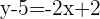

Eine Gerade verläuft durch den Punkt  und hat die Steigung
und hat die Steigung  . Stelle die explizite Form der Geradengleichung auf.
. Stelle die explizite Form der Geradengleichung auf.
Eine Gerade verläuft durch den Punkt  und hat die Steigung
und hat die Steigung  . Stelle die explizite Form der Geradengleichung auf:
. Stelle die explizite Form der Geradengleichung auf:
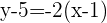
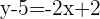
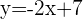
Stelle die Gleichung der Geraden auf, die durch 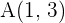 und
und  verläuft.
verläuft.
Stelle die Gleichung der Geraden auf, die durch 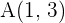 und
und  verläuft.
verläuft.

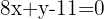
Stelle alle möglichen Arten der Gleichung der Geraden dar, die durch die Punkte  und
und 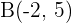 verläuft.
verläuft.
Stelle alle möglichen Arten der Gleichung der Geraden dar, die durch die Punkte  und
und 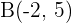 verläuft.
verläuft.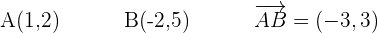
Gleichung einer Geraden, die durch zwei Punkte verläuft


Gleichung in Punkt-Richtungsform
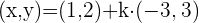
Gleichungen in Parameterform
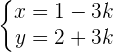
Gleichung in Hauptform

Gleichung in allgemeiner Form

Gleichung in expliziter Form

Gleichung in Punkt-Steigungsform

Ermittle die Steigung und den y-Achsenabschnitt der Geraden  .
.
Ermittle die Steigung und den y-Achsenabschnitt der Geraden 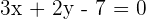 .
.
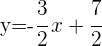

Untersuche die Lagebeziehungen der Geraden anhand der Geradengleichungen:
a 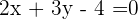
b 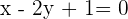
c 
d 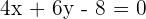
e 
f 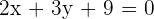
Untersuche die Lagebeziehungen der Geraden anhand der Geradengleichungen:
a 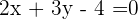
b 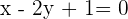
c 
d 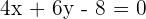
e 
f 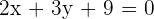
Die Geraden  und
und  sind deckungsgleich, da alle Koeffizienten proportional zueinander sind:
sind deckungsgleich, da alle Koeffizienten proportional zueinander sind:

Die Geraden  und
und  ,
,  und
und  , sowie
, sowie  und
und  sind parallel, da ihre Koeffizienten
sind parallel, da ihre Koeffizienten  und
und  proportional sind, aber nicht ihr konstantes Glied.
proportional sind, aber nicht ihr konstantes Glied.
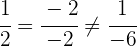
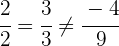

Sind die Geraden 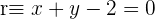 und
und 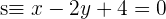 Sekanten?
Sekanten?
Falls ja, berechne ihren Schnittpunkt.
Sind die Geraden 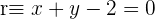 und
und 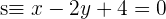 Sekanten? Falls ja, berechne ihren Schnittpunkt:
Sekanten? Falls ja, berechne ihren Schnittpunkt: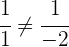 , das heißt die Geraden sind Sekanten.
, das heißt die Geraden sind Sekanten.

Bestimme, welche Art von Dreieck durch die Punkte  ,
, 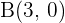 und
und 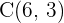 gegeben ist.
gegeben ist.
Bestimme, welche Art von Dreieck durch die Punkte  ,
, 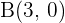 und
und 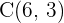 gegeben ist:
gegeben ist:
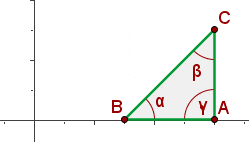

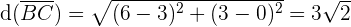
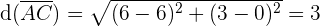
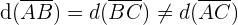 , daher ist das Dreieck gleichschenklig
, daher ist das Dreieck gleichschenklig
 , daher ist das Dreieck rechtwinklig.
, daher ist das Dreieck rechtwinklig.
Bestimme, welche Art von Dreieck durch die Punkte  ,
, 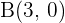 und
und  gegeben ist.
gegeben ist.
Bestimme, welche Art von Dreieck durch die Punkte  ,
, 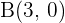 und
und  gegeben ist:
gegeben ist:
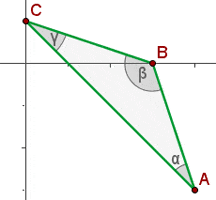

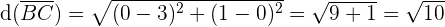
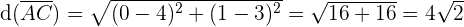
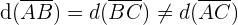 Das Dreieck ist gleichschenklig
Das Dreieck ist gleichschenklig
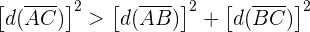 Das Dreieck ist stumpfwinklig
Das Dreieck ist stumpfwinklig
Wir kennen die Punkte 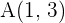 ,
, 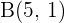 und
und 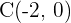 eines Paralellogramms
eines Paralellogramms  .
.
Welche Koordinaten hat der Scheitelpunkt  ?
?
Wir kennen die Punkte 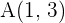 ,
, 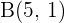 und
und 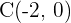 eines Paralellogramms
eines Paralellogramms  . Welche Koordinaten hat der Scheitelpunkt
. Welche Koordinaten hat der Scheitelpunkt  ?
?
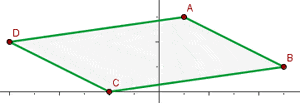

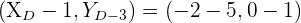
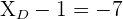
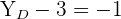

Gegeben ist ein Viereck  mit den Scheitelpunkten
mit den Scheitelpunkten 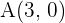 ,
, 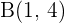 ,
,  und
und 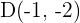 .
.
Prüfe, ob das Viereck ein Parallelogramm ist und bestimme seinen Mittelpunkt und seine Fläche.
Gegeben ist ein Viereck  mit den Scheitelpunkten
mit den Scheitelpunkten 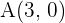 ,
, 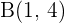 ,
,  und
und 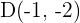 . Prüfe, ob das Viereck ein Parallelogramm ist und bestimme seinen Mittelpunkt und seine Fläche:
. Prüfe, ob das Viereck ein Parallelogramm ist und bestimme seinen Mittelpunkt und seine Fläche:
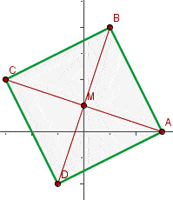

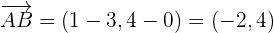
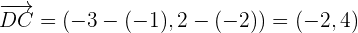


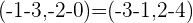
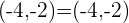
Es ist ein Parallelogramm
Der Mittelpunkt liegt dort, wo sich seine Diagonalen schneiden:

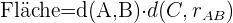
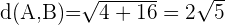



Wir kennen den Scheitelpunkt  eines Parallelogramms und den Schnittpunkt der Diagonalen:
eines Parallelogramms und den Schnittpunkt der Diagonalen:  .
.
Wir wissen auch, dass sich ein anderer Scheitelpunkt im Koordinatenursprung befindet. Bestimme:
a Die anderen Scheitelpunkte.
b Die Gleichungen der Diagonalen.
c Die Länge der Diagonalen.
Wir kennen den Scheitelpunkt  eines Parallelogramms und den Schnittpunkt der Diagonalen:
eines Parallelogramms und den Schnittpunkt der Diagonalen:  . Wir wissen auch, dass sich ein anderer Scheitelpunkt im Koordinatenursprung befindet.
. Wir wissen auch, dass sich ein anderer Scheitelpunkt im Koordinatenursprung befindet.
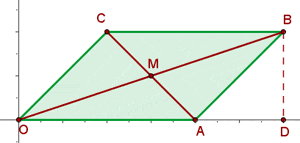
a Bestimme die anderen Scheitelpunkte:
 ist der Mittelpunkt von
ist der Mittelpunkt von 

 ist der Mittelpunkt von
ist der Mittelpunkt von 

b Bestimme die Gleichungen der Diagonalen:
Die Gleichung von  ist:
ist:
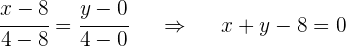
Die Gleichung von  ist:
ist:
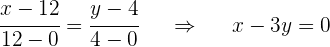
c Die Länge der Diagonalen ist:


Bestimme die Gleichung der Geraden  , die durch
, die durch  verläuft und parallel zur Geraden
verläuft und parallel zur Geraden 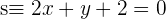 ist.
ist.
Bestimme die Gleichung der Geraden  , die durch
, die durch  verläuft und parallel zur Geraden
verläuft und parallel zur Geraden 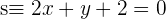 ist.
ist.
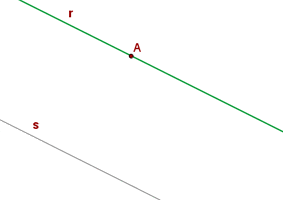



Stelle die Gleichung der Geraden auf, die durch  verläuft und parallel zur Geraden ist, die zwischen den Punkten
verläuft und parallel zur Geraden ist, die zwischen den Punkten  und
und  verläuft.
verläuft.
Stelle die Gleichung der Geraden auf, die durch  verläuft und parallel zur Geraden ist, die zwischen den Punkten
verläuft und parallel zur Geraden ist, die zwischen den Punkten  und
und  verläuft:
verläuft:

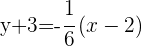

Die Gerade  verläuft durch den Punkt
verläuft durch den Punkt  und ist parallel zur Geraden
und ist parallel zur Geraden  .
.
Berechne  und
und  .
.
Die Gerade  verläuft durch den Punkt
verläuft durch den Punkt  und ist parallel zur Geraden
und ist parallel zur Geraden  . Berechne
. Berechne  und
und  :
:
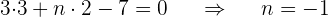

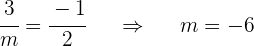
Gegeben ist das Dreieck  mit den Koordinaten
mit den Koordinaten  ,
,  und
und  . Berechne die Gleichung des Medians, der durch den Scheitelpunkt
. Berechne die Gleichung des Medians, der durch den Scheitelpunkt  verläuft.
verläuft.
Gegeben ist das Dreieck  mit den Koordinaten
mit den Koordinaten  ,
,  und
und  . Berechne die Gleichung des Medians, der durch den Scheitelpunkt
. Berechne die Gleichung des Medians, der durch den Scheitelpunkt  verläuft:
verläuft: 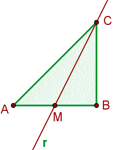

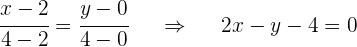
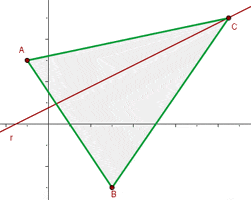
Die Punkte  und
und  sind Scheitelpunkte des gleichschenkligen Dreiecks
sind Scheitelpunkte des gleichschenkligen Dreiecks  , dessen Scheitelpunkt
, dessen Scheitelpunkt  auf der Geraden
auf der Geraden  liegt und dessen Seiten
liegt und dessen Seiten  und
und  gleich lang sind.
gleich lang sind.
Berechne die Koordinaten des Scheitelpunkts  .
.
Die Punkte  und
und  sind Scheitelpunkte des gleichschenkligen Dreiecks
sind Scheitelpunkte des gleichschenkligen Dreiecks  , dessen Scheitelpunkt
, dessen Scheitelpunkt  auf der Geraden
auf der Geraden  liegt und dessen Seiten
liegt und dessen Seiten  und
und  gleich lang sind. Berechne die Koordinaten des Scheitelpunkts
gleich lang sind. Berechne die Koordinaten des Scheitelpunkts  :
:
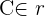

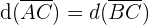

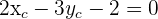
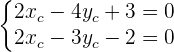
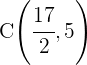
Mit KI zusammenfassen:



