Mittelsenkrechte einer Strecke
Die Mittelsenkrechte ist der geometrische Ort, an dem sich die Punkte der Ebene befinden, die von den Endpunkten gleich weit entfernt sind.
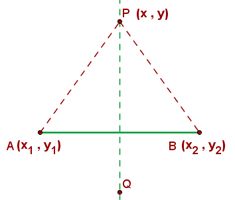
Gleichung der Mittelsenkrechte
Um die Gleichung der Mittelsenkrechte zu bestimmen, führen wir folgende Schritte durch:
1Der Abstand von einem Punkt 
auf der Mittelsenkrechte zu den Endpunkten 
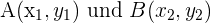der Strecke ist gleich
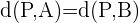
2Wir schreiben in Bezug auf die Koordinaten von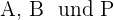 
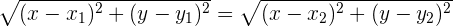
3Wir setzen die Radikanden gleich und erhalten so die Gleichung der Mittelsenkrechte
Beispiel
Ermittle die Gleichung der Mittelsenkrechte der Strecke mit den Endpunkten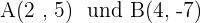 
.
1Der Abstand von einem Punkt auf der Mittelsenkrechte zu den Endpunkten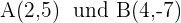 
der Strecke ist gleich
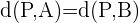
2Wir schreiben in Bezug auf die Koordinaten von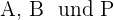
3Wir setzen die Radikanden gleich und erhalten so die Gleichung der Mittelsenkrechten
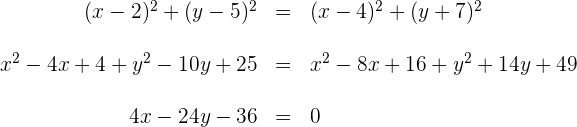
4Wir vereinfachen die letzte erhaltene Gleichung und diese ist die Gleichung der Mittelsenkrechte.
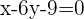
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
