Kapitel
Höhen eines Dreiecks
Die Höhen eines Dreiecks sind die senkrechten Geraden, die von einem Eckpunkt zur gegenüberliegenden Seite (oder deren Verlängerung) gezogen werden.
Höhenschnittpunkt
Der Höhenmittelpunkt ist der Punkt, in dem sich die drei Höhen schneiden.
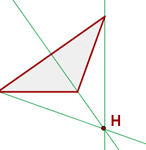
Der Höhenschnittpunkt wird mit dem Buchstaben H gekennzeichnet.
Eulersche Gerade
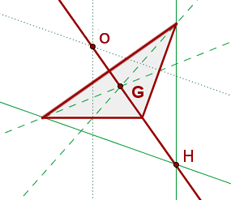
Der Höhenschnittpunkt, der Schwerpunkt und der Umkreismittelpunkt eines nicht gleichseitigen Dreiecks befinden sich auf einer Linie. Das heißt, sie befinden sich auf derselben Geraden, der Eulerschen Geraden.
Lage des Höhenschnittpunkts
Die Lage des Höhenschnittpunkts hängt von der Klassifizierung des Dreiecks nach seinen Winkeln ab:
Spitzwinklig
In einem spitzwinkligen Dreieck befindet sich der Höhenschnittpunkt im Inneren des Dreiecks.
Stumpfwinklig
Bei einem stumpfen Dreieck liegt der Höhenschnittpunkt außerhalb des Dreiecks, da sich einige Höhen außerhalb des Dreiecks befinden.
Rechtwinklig
Bei einem rechtwinkligen Dreieck befindet sich der Höhenschnittpunkt im Scheitelpunkt des rechten Winkels.
Beispielaufgabe mit Lösung
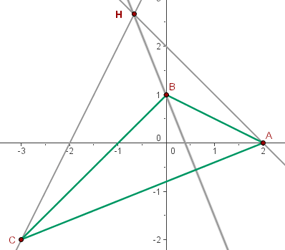
Ermittle die Gleichungen der Höhen und den Höhenschnittpunkt des Dreiecks: 
, 
und 
.
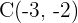Was du wissen musst:
Die Gleichung einer Geraden mit der Steigung 
, die durch den Punkt 
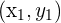verläuft, lautet:
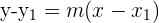
Diese nennt man Punkt-Steigungs-Form.
Wenn wir eine Gerade haben, die durch die Punkte 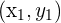und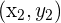 
verläuft, ist ihre Steigung:
Wenn zwei Geraden zueinander senkrecht sind, gilt für ihre Steigungen:
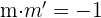
Lösen von linearen Gleichungssystemen mit zwei Unbekannten
Gleichung der Höhe, die durch den Eckpunkt A verläuft
Um die Gleichung einer Geraden zu berechnen, müssen wir ihre Steigung und einen Punkt kennen, durch den sie verläuft. EIm Falle der durch A verlaufenden Höhe kennen wir ihre Steigung nicht, aber wir wissen, dass sie senkrecht auf der gegenüberliegenden Seite (Seite BC) steht. Wir ermitteln also zunächst die Steigung der Seite BC.
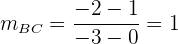
Da die Höhe von A und die Seite BC senkrecht zueinander sind, gilt für ihre Steigungen
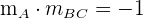
Wir setzen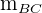 
ein und bestimmen 
Die Höhe, die durch verläuft, hat die Steigung . Wir wenden die Punkt-Steigungs-Form an
Gleichung der Höhe, die durch den Eckpunkt B verläuft
Wir gehen in ähnlicher Weise vor wie im vorherigen Fall. Zuerst ermitteln wir die Steigung der Seite gegenüber von B, der Seite AC.
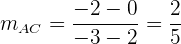
Da die Höhe von B und die Seite AC zueinander senkrecht sind, gilt für ihre Steigungen
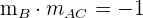
Wir setzen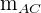 
ein und bestimmen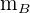 
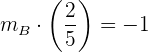
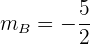
Die Höhe, die durch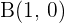 
verläuft, hat die Steigung 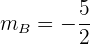. Wir wenden die Punkt-Steigungs-Form an
Gleichung der Höhe, die durch den Eckpunkt C verläuft
Die gebenüberliegende Seite von C ist AB. Ihre Steigung ist:
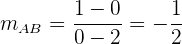
Da die Höhe von C und die Seite AB senkrecht zueinander sind, gilt für ihre Steigungen
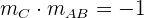
Sustituimos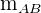 
und bestimmen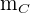 
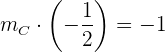
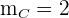
Die Höhe, die durch 
verläuft, hat die Steigung 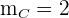. Wir wenden die Punkt-Steigungs-Form an
Höhenschnittpunkt
Der Höhenschnittpunkt ist der Schnittpunkt der drei Höhen. Um ihn zu berechnen, lösen wir das Gleichungssystem, das die zwei Gleichungen bilden.
Wenn du noch unsicher bist, wie du dieses Gleichungssystem lösen kannst, empfehlen wir dir unsere Artikel über das Additionsverfahren, das Gleichsetzungsverfahren oder das Einsetzungsverfahren.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
