Kapitel
- Geraden, die durch einen Punkt und einen Vektor definiert sind
- Identische Geraden
- Parallele Geraden
- Sich schneidende Geraden
- Windschiefe Geraden
- Geraden, die durch ihre implizite Darstellung der Gleichung definiert sind
- Lagebeziehung zwischen einer Gerade und einer Ebene
- Lagebeziehung zwischen zwei Ebenen
- Lagebeziehung zwischen drei Ebenen
Geraden, die durch einen Punkt und einen Vektor definiert sind
Wenn die Gerade 
durch 
und 
gegeben ist, und die Gerade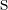 
durch 
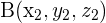und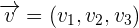 
gegeben ist, ist die Lagebeziehung zwischen und 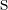durch die Lage von 
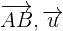und 
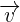gegeben.
Wenn gilt
,
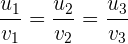gibt es zwei Möglichkeiten:
Identische Geraden
Wenn gilt
,
sind die Geraden identisch.
Identische Geraden sind zwei gerade Linien auf der gleichen Ebene, die alle Punkte gemeinsam haben und somit aufeinander liegen
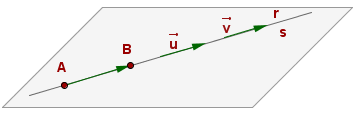
Parallele Geraden
Wenn Folgendes gilt
,
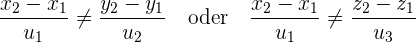sind die Geraden parallel.
Zwei Geraden sind parallel, wenn sie die gleiche Steigung haben oder senkrecht zu einer der Achsen verlaufen.
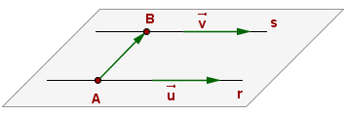
Wenn folgender Fall eintritt
,
gibt es zwei weitere Möglichkeiten:
Sich schneidende Geraden
Zwei Geraden schneiden sich, wenn gilt
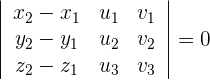
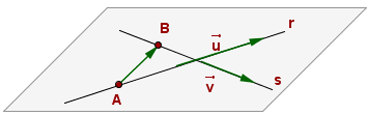
Windschiefe Geraden
Zwei Geraden sind windschief, wenn gilt
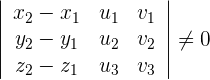
Dies ist der Fall, wenn zwei Geraden nicht in einer Ebene liegen.
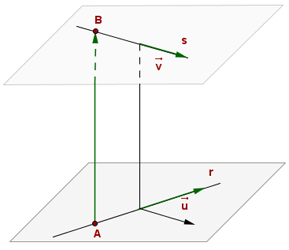
Geraden, die durch ihre implizite Darstellung der Gleichung definiert sind
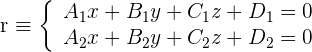
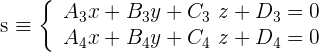
Gegeben ist:
Rang der Koeffizientenmatrix.
Rang der erweiterten Matrix.
Die Lagebeziehung zweier Geraden ist durch folgende Tabelle gegeben:
| Lagebeziehung | r | r' |
|---|---|---|
| windschief | 3 | 4 |
| sich schneidend | 3 | 3 |
| parallel | 2 | 3 |
| identisch | 2 | 2 |
Lagebeziehung zwischen einer Gerade und einer Ebene
1. Die Gerade ist durch einen Punkt und einen Vektor definiert
Gegeben ist eine Gerade, die durch den Punkt 
und den Vektor 
sowie eine Ebene mit dem Normalenvektor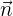 
gegeben. Die Lagenbeziehungen zwischen der Gerade und der Ebene sind:
| Lagebeziehung |  | |
|---|---|---|
| Gerade in der Ebene | !ERROR! illegal character '[' |  |
| Gerade und Ebene sind parallel | !ERROR! illegal character '[' |  |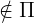
| Gerade und Ebene schneiden sich | ≠  |
2. Die Gerade ist durch zwei sich schneidende Ebenen gegeben
Gegeben ist die Gerade:
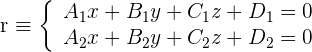
und die Ebene:
Um die Lagebeziehung zwischen der Gerade und der Ebene zu untersuchen, sehen wir uns folgendes System an:
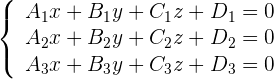
Und:
Rang der Koeffizientenmatrix.
Rang der erweiterten Matrix.
Die Lagebeziehungen zwischen der Gerade und der Ebene sind durch folgende Tabelle gegeben:
| Lagebeziehung | |  |
| Gerade in der Ebene |  | |
| Gerade und Ebene sind parallel | |  |
| Gerade und Ebene schneiden sich | | |
Lagebeziehung zwischen zwei Ebenen
Gegeben sind die Ebenen:
Und:
Rang der Koeffizientenmatrix.
Rang der erweiterten Matrix.
Die Lagebeziehungen zwischen den zwei Ebenen sind durch folgende Tabelle gegeben:
| | Lagebeziehung | |
|---|---|---|---|
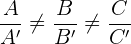| |  | sich schneidend |
 | |  | parallel |
| |  | identisch |
Lagebeziehung zwischen drei Ebenen
Um die Lagebeziehungen zwischen drei Ebenen zu untersuchen, sehen wir uns folgendes System an:
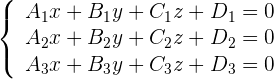
Und:
Rang der Koeffizientenmatrix.
Rang der erweiterten Matrix.
Die Lagebeziehungen zwischen den drei Ebenen sind durch folgende Tabelle gegeben:
| r | r′ | Bedingung | Lagebeziehung |
|---|---|---|---|
| 3 | 3 | – | 1. Ebenen schneiden sich in einem Punkt. |
| 2 | 3 | | 2.1 Jeweils zwei Ebenen schneiden sich. 2.2 Zwei Ebenen sind parallel, die dritte Ebene schneidet. |
| 2 | 2 | | 3.1 Die Ebenen schneiden sich, sind nicht identisch. 3.2 Zwei identische Ebenen, eine Ebene schneidet. |
| 1 | 2 | | 4.1 Parallele, nicht identische Ebenen. 4.2 Parallele Ebenen, zwei Ebenen sind identisch. |
| 1 | 1 | – | 5. Identische Ebenen. |
Beispiele
Bestimme die Lagebeziehung zwischen den Geraden und .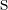
1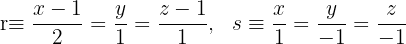 
Zunächst bringen wir die Gleichungen in die implizite Form:
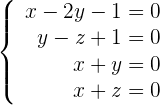
Wir bestimmen den Rang der Koeffizientenmatrix.
Wir bestimmen den Rang der erweiterten Matrix.
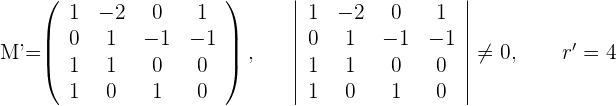
Wir überprüfen die Ränge.
Wir sehen uns die Tabelle an und kommen zu dem Schluss, dass die zwei Geraden windschief sind.
2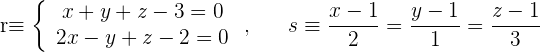 
Zunächst bringen wir die Gleichungen in die implizite Form.
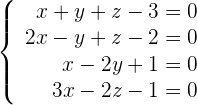
Wir bestimmen den Rang der Koeffizientenmatrix.
Wir bestimmen den Rang der erweiterten Matrix.
Wir überprüfen die Ränge.
Wir sehen uns die Tabelle an und kommen zu dem Schluss, dass die zwei Geraden windschief sind.
Wir überprüfen die Ränge.
Wir sehen uns die Tabelle an und kommen zu dem Schluss, dass die zwei Geraden sich schneiden.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
