Der Mittelpunkt und seine Koordinaten
Der Mittelpunkt ist der Punkt, der sich in gleichem Abstand zu zwei anderen beliebigen Punkten oder Endpunkten eines Segments befindet. Bei einem Segment ist der Mittelpunkt der Punkt, der es in zwei gleiche Teile teilt.
und 
sind die Endpunkte eines Segments. Der Mittelpunkt des Segements ist wie folgt gegeben:
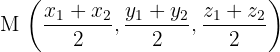
Beispiele für die Berechnung des Mittelpunktes
1 Gegeben sind die Punkte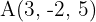 
und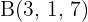 
. Berechne die Koordinaten des Mittelpunktes des Segments.
Wir wenden die Formel für die Koordinaten des Mittelpunktes an und erhalten
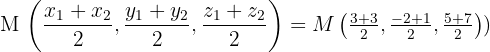
und somit:
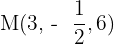
2Die Koordinaten der aufeinanderfolgenden Eckpunkte eines Parallelogramms si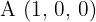nd 
und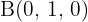 
. Die Koordinaten des Mittelpunktes 
sind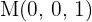 
. Berechne die Koordinaten der Eckpunkte 
und 
.
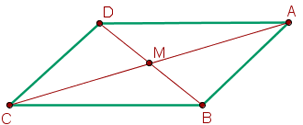
Wir stellen fest, dass der Mittelpunkt zwischen den Eckpunkten 
und ist, aber auch der Mittelpunkt zwischen den Eckpunkten 
und .
Da es sich um einen Mittelpunkt handelt, muss er der Formel für die Koordinaten des Mittelpunkts entsprechen. Wir verwenden diese, um die übrigen Eckpunkte zu berechnen.
Eckpunkt C:
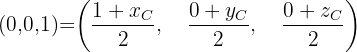
und somit:
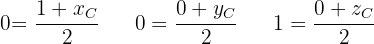
Also
das heißt, der Eckpunkt C ist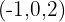 
.
Eckpunkt D:
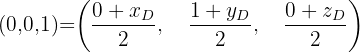
und somit:
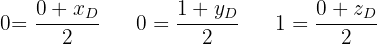
Also
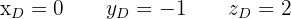
also erhalten wir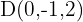 
.
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
