Definition und Eigenschaften orthogonaler Geraden
Zwei Geraden nennt man orthogonal, wenn der Winkel, der zwischen ihnen liegt 
beträgt. Betrachte die folgende Abbildung:
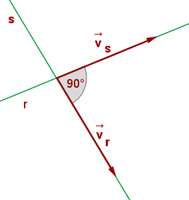
Geraden einer Ebene
Zwei Geraden 
und 
, die im zweidimensionalen Raum liegen, sind dann orthogonal, wenn eine der folgenden Bedingungen erfüllt sind:
1 Das Produkt der Steigungen ist gleich 
:
auch
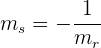
2 Die Richtungsvektoren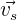 
und 
der Geraden sind orthogonal (d.h. ihr Produkt ist gleich 0):
Anmerkung: orthogonale Geraden in einer Ebene besitzen immer einen einzigen Schnittpunkt. Die Tatsache, dass sich zwei Geraden an einem Punkt schneiden genügt aber nicht, um zu beweisen, dass sie auch orthogonal sind.
Geraden im Raum
Wenn zwei Geraden und sich im Raum befinden, kann man nur feststellen, ob sie orthogonal sind, indem man das interne Produkt ihrer Richtungsvektoren berechnet. Dieses Produkt muss gleich 0 sein:
Anmerkung: im Fall von Geraden im Raum ist es möglich, dass sich bestimmte orthogonale Geraden niemals schneiden.
Anmerkung: eine Gerade besitzt unendlich viele orthogonale Geraden. Wenn wir eine Gerade finden wollen, für die 
gilt, müssen wir weitere Nebenbedingungen kennen (z.B. einen Punkt, durch den die Gerade außerdem verläuft).
Rechenbeispiele: orthogonale Geraden
Die Gerade ist orthogonal zu 
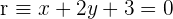und verläuft durch den Punkt 
. Ermittle die Geradengleichung
Da es um eine Gerade auf der Ebene geht, können wir die Steigung von bestimmen:
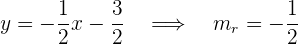
Die Steigung von ist
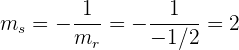
Mithilfe der Punkt-Steigungs-Formel der Geraden erhalten wir
Die Gleichung der orthogonalen Geraden ist also
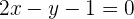
Ermittle die Gleichung der Geraden, die orthogonal zu 
ist und durch den Punkt 
verläuft.
Da die Gerade auf einer Ebene liegt, können wir die Steigung berechnen:
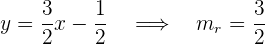
Die Steigung der Geraden ist
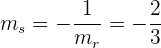
Mithilfe der Punkt-Steigungs-Formel der Geraden erhalten wir für
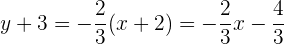
Die Gleichung der Geraden ist also
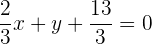
Die Gleichung kann mit 3 multipliziert werden, um die Brüche aufzuheben:
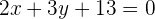
Gegeben sind die Geraden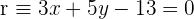 
und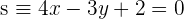 
. Bestimme die Gleichung der Geraden, die durch den Schnittpunkt von und verläuft und außerdem orthogonal zu 
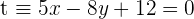ist.
Um die Gerade 
zu ermitteln, die orthogonal zu 
ist, müssen wir zuerst den Punkt herausfinden, durch den sie verläuft. Den Schnittpunkt von und finden wir heraus, indem wir das folgende Gleichungssystem auflösen:
Wir stellen die zweite Gleichung nach 
um und erhalten
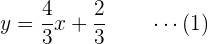
Das Ergebnis setzen wir in die erste Gleichung ein:
das heißt 
. Durch Einsetzen in die erste Gleichung erhalten wir 
.
Die Gerade verläuft also durch den Punkt 
.
Die Steigung von ist
das heißt, die Steigung von ist gleich
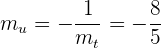
Jetzt verwenden wir die Punkt-Steigungs-Formel:
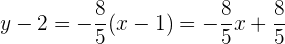
Wir multiplizieren beide Seiten der Gleichung mit 5:
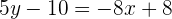
Die Gleichung der Geraden , die orthogonal zu ist, ist also
Für welchen Wert von 
sind die Geraden 
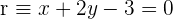und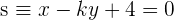 
orthogonal?
Damit die Geraden orthogonal sind, muss das Produkt ihrer Steigungen gleich sein. Zuerst müssen wir also die Steigungen von und von herausfinden:
und von ,
Durch Multiplizieren der Steigungen erhalten wir
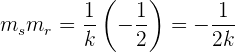
Da das Ergebnis sein muss, ist
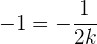
Wir lösen nach auf und erhalten 
oder
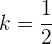
Für den Wert = 
sind die Geraden also orthogonal.
Gegeben sind zwei Geraden im Raum:
und
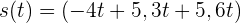
Sind und orthogonal?
Die Gerade kann auch wie folgt umgeschrieben werden:
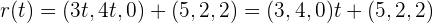
Der Richtungsvektor von ist daher
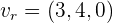
Ähnlich kann auch die Gerade umgeschrieben werden:
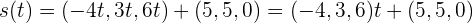
Ihr Richtungsvektor ist
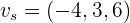
Das interne Produkt von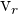 
und 
ist
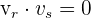, daher sind 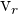und orthogonal.
Wir kommen zu dem Ergebnis, dass und orthogonal sind.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
