Zwei Geraden in der Ebene können sein:
Sekanten
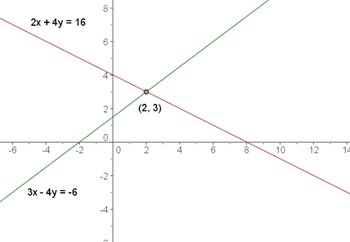
Zwei Geraden sind Sekanten, wenn sie nur einen Punkt gemeinsam haben.
Das Gleichungssystem, das aus den beiden Geraden gebildet wird, hat eine Lösung.
Parallelen
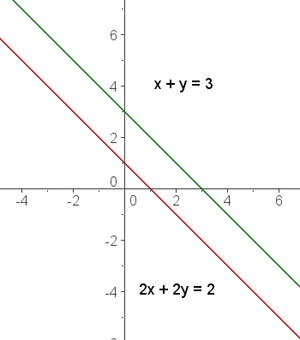
Zwei Geraden sind parallel, wenn sie keinen gemeinsamen Punkt haben.
El sistema de ecuaciones formado por las dos rectas no tiene solución.
Identisch
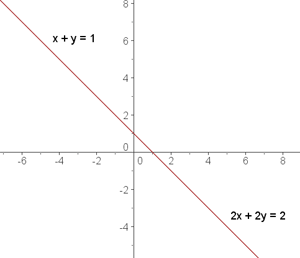
Zwei Geraden sind identisch, wenn sie alle Punkte gemeinsam haben.
Das Gleichungssystem, das aus den beiden Geraden gebildet wird, hat unendlich viele Lösungen.
| Explizite Gleichung | Allgemeine Gleichung | |
|---|---|---|
| r und s sind Sekanten |  |  |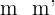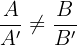
| r und s sind parallel |   |  |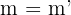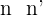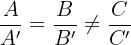
| r und s sind identisch |  |  |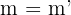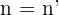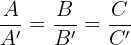
Untersuche die Lagebeziehungen der folgenden Geradenpaare:
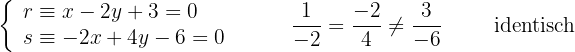
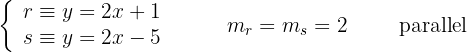
Untersuche die Lagebeziehungen der Geraden der Gleichungen:
1
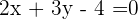
2
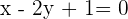
3
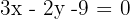
4
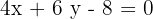
5
6
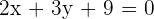
Die Geraden 1 und 4 sind identisch, da alle ihre Koeffizienten proportional sind:
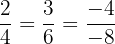
Die Geraden 2 und 5 sowie 1 und 6 sind jeweils parallel, da zwischen den Koeffizienten von x und y eine Proportionalität besteht, jedoch nicht beim unabhängigen Term.
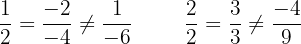
Sind die Geraden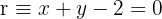 
und 
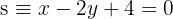Sekanten? Falls ja, berechne ihren Schnittpunkt
Gegeben sind die Geraden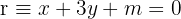 
und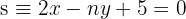 
. Berechne 
und 
, so dass:
1
Sie parallel sind.
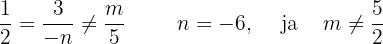
2
Sie sich im Punkt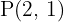 
schneiden.
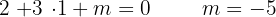
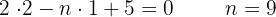
3
Sie identisch sind.
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
